Bốn đồ thị nói trên cắt nhau tại các điểm \(O\left( {0;0} \right),A,B,C\). Tứ giác có bốn đỉnh \(O;A;B;C\) là hình gì? Giải thích.

Những câu hỏi liên quan
Cho 2 hàm số bậc nhất y=-2x+k và y=3x-k+4. Với giá trị nào của k thì: a) Đồ thị của các hàm số trên cắt nhau tại một điểm nằm trên trục tung. b) Đồ thị của các hàm số trên cắt nhau tại một điểm nằm trên trục hoành
Tọa độ giao điểm của \(y=-2x+k\) và trục hoành: \(y=0\Rightarrow x=\dfrac{k}{2}\)
Tọa độ giao điểm \(y=-2x+k\) với trục tung: \(x=0\Rightarrow y=k\)
Tọa độ giao điểm của \(y=3x-k+4\) với trục hoành: \(y=0\Rightarrow x=\dfrac{k-4}{3}\)
Tọa độ giao điểm của \(y=3x-k+4\) với trục tung: \(x=0\Rightarrow y=-k+4\)
a. Đồ thị các hàm cắt nhau tại 1 điểm trên trục tung khi:
\(k=-k+4\Rightarrow x=2\)
b. Đồ thị các hàm cắt nhau tại 1 điểm trên trục hoành khi:
\(\dfrac{k}{2}=\dfrac{k-4}{3}\Rightarrow k=-8\)
Đúng 0
Bình luận (1)
* Điều kiện để 2 đồ thị hàm số vuông góc với nhau.* Điều kiện để 2 đồ thị hàm số cắt nhau tại 1 điểm trên trục hoành.* Điều kiện để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung.* Điều kiện để 2 đồ thị hàm số song song với nhau.* Điều kiện để 2 đồ thị hàm số cắt nhau.* Điều kiện để 2 đồ thị hàm số trùng nhau.* Điều kiện để 2 đồ thị hàm số song song và cắt nhau trên trục tung
Đọc tiếp
* Điều kiện để 2 đồ thị hàm số vuông góc với nhau.
* Điều kiện để 2 đồ thị hàm số cắt nhau tại 1 điểm trên trục hoành.
* Điều kiện để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung.
* Điều kiện để 2 đồ thị hàm số song song với nhau.
* Điều kiện để 2 đồ thị hàm số cắt nhau.
* Điều kiện để 2 đồ thị hàm số trùng nhau.
* Điều kiện để 2 đồ thị hàm số song song và cắt nhau trên trục tung
* Điều kiện để 2 đồ thị hàm số vuông góc với nhau.a.a'=-1
* Điều kiện để 2 đồ thị hàm số cắt nhau tại 1 điểm trên trục hoành.a khác a'
và b/a khác b'/a'
* Điều kiện để 2 đồ thị hàm số cắt nhau tại một điểm trên trục tung a khác a'
và b=b'
* Điều kiện để 2 đồ thị hàm số song song với nhau a=a'
và b khác b'
* Điều kiện để 2 đồ thị hàm số cắt nhau.a khác a'
* Điều kiện để 2 đồ thị hàm số trùng nhau.a=a' và b=b'
* Điều kiện để 2 đồ thị hàm số song song và cắt nhau trên trục tung kết hợp lần lượt of 2 điều kiện
Đúng 1
Bình luận (0)
Theo mk nhớ thì đã song song làm sao cắt nhau được hả bạn?
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Bài 1. yleft(m-frac{2}{3}right)x+1left(dright) yleft(2-mright)x-3left(dright)Bài 2. Viết phương trình của đường thẳng thõa mãn điều kiện sau:a) Đi qua hai điểm M(1;2) và N(3;6)b) Cắt trục hoành tại điểm Aleft(frac{2}{3};0right) và cắt trục tung tại điểmBleft(0;3right)Bài 3: yleft(k-2right)x+kleft(kne2right)left(dright)yleft(k+3right)x-kleft(kne-3right)left(dright)Với giá trị nào của k thì:a) Đồ thị của các hàm số trên cắt nhau tại một điểm trên trục tungb) Đồ thị của các hàm số trên cắt nhau tại...
Đọc tiếp
Bài 1. \(y=\left(m-\frac{2}{3}\right)x+1\left(d\right) \)
\(y=\left(2-m\right)x-3\left(d'\right)\)
Bài 2. Viết phương trình của đường thẳng thõa mãn điều kiện sau:
a) Đi qua hai điểm M(1;2) và N(3;6)
b) Cắt trục hoành tại điểm \(A\left(\frac{2}{3};0\right)\) và cắt trục tung tại điểm\(B\left(0;3\right)\)
Bài 3: \(y=\left(k-2\right)x+k\left(k\ne2\right)\left(d\right)\)
\(y=\left(k+3\right)x-k\left(k\ne-3\right)\left(d'\right)\)
Với giá trị nào của k thì:
a) Đồ thị của các hàm số trên cắt nhau tại một điểm trên trục tung
b) Đồ thị của các hàm số trên cắt nhau tại một điểm trên trục hoành
Bài 4. Vẽ đồ thị hàm số y = | 1 - 3x | (phân tích, hướng dẫn cách vẽ)
a) Vẽ đồ thị của các hàm số y x và y 2x + 2 trên cùng một mặt phẳng tọa độ.b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y x tại điểm C. Tìm tọa độ điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)
Đọc tiếp
a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.
b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.
c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
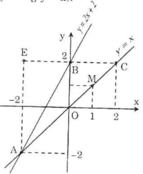
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
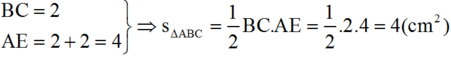
Đúng 1
Bình luận (0)
a)
+) y = 2x + 2
Cho x = 0 => y = 2
=> ( 0 ; 2 )
y = 0 => x = -1
=> ( -1 ; 0 )
- Đồ thị hàm số y = x đi qua 2 điểm có tọa độ ( 0 ; 0 )
- Đồ thị hàm số y = 2x + 2 đi qua 2 điểm có tọa độ ( 0 ; 2 ) và ( -1 ; 0 )
b) Hoành độ điểm A là nghiệm của PT sau :
x = 2x + 2
<=> 2x - x = -2
<=> x = -2
=> y = -2
Vậy A ( -2 ; -2 )
c) Tung độ điểm C = 2 => hoành độ điểm C là x = 2
=> C ( 2 ; 2 )
Từ A hạ \(AH\perp BC\), ta có : AH = 4cm
BC = 2cm
Vậy : ..............
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.4.2=4\left(cm^2\right)\)
Giả sử
F
x
là nguyên hàm của hàm số
f
x
4
x
-
1
. Đồ thị hàm số
F
x
và
f
x
cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là: A.
0
;
-
1...
Đọc tiếp
Giả sử F x là nguyên hàm của hàm số f x = 4 x - 1 . Đồ thị hàm số F x và f x cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
A. 0 ; - 1
B. 5 2 ; 8
C. 0 ; - 1 và 5 2 ; 9
D. 5 2 ; 9
Cho hai hàm số đa thức bậc bốn yf(x)và yg(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số yf(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [-3;3] bằng A.
12
-
8
3
9
B. ...
Đọc tiếp
Cho hai hàm số đa thức bậc bốn y=f(x)và y=g(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y=f(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [-3;3] bằng
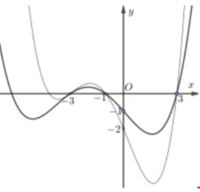
A. 12 - 8 3 9
B. - 3
C. 12 - 10 3 9
D. 10 - 9 3 9
Theo giả thiết có ![]()
![]()
Do ![]()
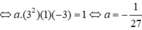
Do đó ![]()
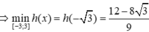
Chọn đáp án A.
Đúng 0
Bình luận (0)
Giả sử F(x) là nguyên hàm của hàm số f(x)4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là A. (0;-1) B.
5
2
;
8
C.
0
;
-
1
v
à
...
Đọc tiếp
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là
A. (0;-1)
B. 5 2 ; 8
C. 0 ; - 1 v à 5 2 ; 9
D. 5 2 ; 9
f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.
Đúng 0
Bình luận (0)
Giả sử F(x) là nguyên hàm của hàm số f(x)4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
Đọc tiếp
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
![]()
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
![]()
![]()
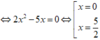
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
![]()
Đúng 0
Bình luận (0)
Cho 2 hàm số y = k + 2 (d1) và y = \(3kx+\left(k-3\right)\) với giá trị nào của k thì Đồ thị của 2 HS trên cắt nhau tại 1 điểm trên trục tung
Gọi A và B lần lượt là giao điểm của \(d_1\) và \(d_2\) với trục tung
\(\Rightarrow\left\{{}\begin{matrix}A\left(0;2\right)\\B\left(0;k-3\right)\end{matrix}\right.\)
Đồ thị 2 hàm số cắt nhau tại 1 điểm trên trục tung khi và chỉ khi A trùng B
\(\Leftrightarrow2=k-3\)
\(\Leftrightarrow k=5\)
Đúng 1
Bình luận (0)













