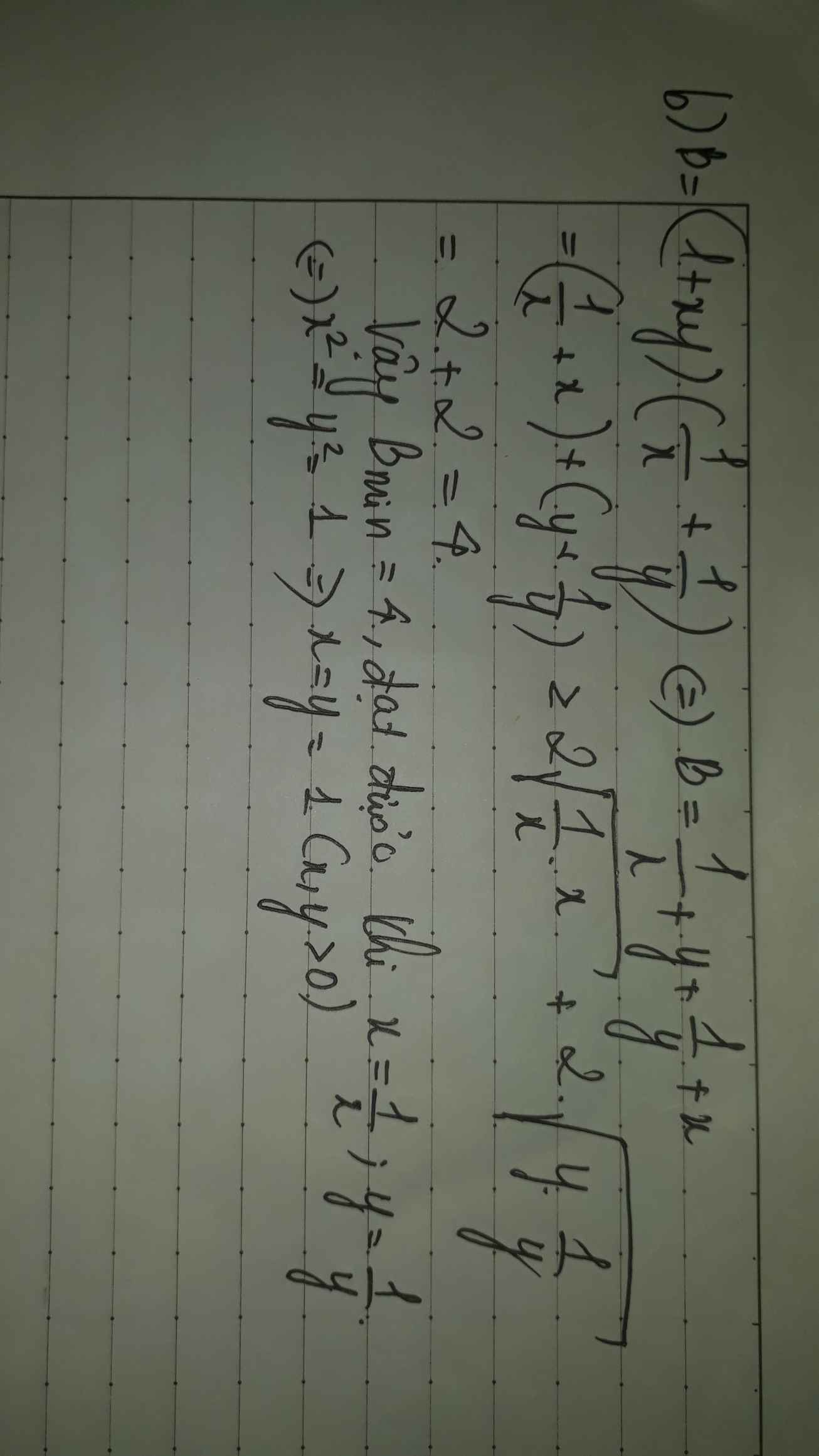2|x+1|+(y+x)2=0
Tìm x; y.

Những câu hỏi liên quan
Tìm x,y thuộc n sao để x^3y-x^2y+4x^2+5xy-y^2=0
tìm số nguyên x,y sao cho x(x^2-y)+y+3)(x^2+1)=0
(1/2.x-7).(x+2)=0
tìm x
`(1/2x-7)(x+2)=0`
`<=>` \(\left[ \begin{array}{l}\dfrac12x-7=0\\x+2=0\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}\dfrac12x=7\\x=-2\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=14\\x=-2\end{array} \right.\)
Vậy `x=14` hoặc `x=-2`
Đúng 1
Bình luận (0)
Ta có: \(\left(\dfrac{1}{2}x-7\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-7=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=14\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
(x-2)3-x(x-1)(x+1)+x(7x-6)=0
Tìm x
Ta có: \(\left(x-2\right)^3-x\left(x-1\right)\left(x+1\right)+x\left(7x-6\right)=0\)
\(\Leftrightarrow x^3-6x^2+12x-8-x^3+x+7x^2-6x=0\)
\(\Leftrightarrow x^2+7x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
bạn có thể tách rõ hơn đoạn cuối dc khum mình cảm ơn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
(x+1)^24 + (y-1)^28 = 0
Tìm x,y
Có \(\left(x+1\right)^{24}\ge0\forall x\)
\(\left(y-1\right)^{28}\ge0\forall y\)
Nên \(\left(x+1\right)^{24}+\left(y-1\right)^{28}\ge0\forall x,y\)
Dấu "=" xảy ra khi \(x=-1,y=1\)
Đúng 2
Bình luận (0)
Ta có:
(x + 1)24 \(\ge\) 0 với mọi x \(\in\) R
(y - 1)28 \(\ge\) 0 với mọi y \(\in\) R
\(\Rightarrow\) (x + 1)24 + (y - 1)28 \(\ge\) 0
\(\Rightarrow\) (x + 1)24 + (y - 1)28 = 0 \(\Leftrightarrow\) (x + 1)24 = 0 và (y - 1)28 = 0
*) (x + 1)24 = 0
x + 1 = 0
x = -1
*) (y - 1)28 = 0
y - 1 = 0
y = 1
Vậy x = -1; y = 1
Đúng 0
Bình luận (0)
x(x+1)-(x-2)(x+1)=0
tìm x
giúp mình với ạ
x(x+1)-(x-2)(x+1)=0
\(\left(x+1\right)\left(x-x+2\right)=0\\ \left(x+1\right)\cdot2=0\\ =>x+1=0\\ x=0-1\\ x=-1\)
Đúng 1
Bình luận (0)
=>(x+1)(x-x+2)=0
=>x+1=0
=>x=-1
Đúng 0
Bình luận (0)
tam giác abc có;
C(0;-2)
đường cao AH : x+2y-1=0
trung điểm BN -x+y=0
tìm tọa độ A,B
Đường thẳng BC qua C và vuông góc AH nên nhận (2;-1) là 1 vtpt
Phương trình BC:
\(2\left(x-0\right)-1\left(y+2\right)=0\Leftrightarrow2x-y-2=0\)
B là giao điểm BN và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}-x+y=0\\2x-y-2=0\end{matrix}\right.\) \(\Rightarrow B\left(2;2\right)\)
Do A thuộc AH nên tọa độ có dạng: \(A\left(-2a+1;a\right)\)
N là trung điểm AC \(\Rightarrow N\left(\dfrac{-2a+1}{2};\dfrac{a-2}{2}\right)\)
N thuộc BN nên: \(-\dfrac{-2a+1}{2}+\dfrac{a-2}{2}=0\)
\(\Leftrightarrow a=1\Rightarrow A\left(-1;1\right)\)
Đúng 2
Bình luận (0)
\(\dfrac{1}{3}x\)+\(\dfrac{2}{3}\)(x-1)=0
tìm x
\(\dfrac{1}{3}x+\dfrac{2}{3}\left(x-1\right)=0\\ \dfrac{1}{3}x+\dfrac{2}{3}x-\dfrac{2}{3}=0\\ x=\dfrac{2}{3}\)
Đúng 3
Bình luận (0)
`1/3x + 2/3(x-1) =0`
` 1/3x + 2/3x -2/3 = 0`
` ( 1/3 + 2/3) x -2/3 = 0`
` 3/3x -2/3 = 0`
` 1x-2/3 = 0`
`1/x = 0 + 2/3`
` 1x = 2/3`
` x = 2/3`
Đúng 4
Bình luận (1)
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện x+yle1. Chứng minhx^2-frac{3}{4x}-frac{x}{y}lefrac{-9}{4}Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+yge1và x0Tìm giá trị nhỏ nhất của biểu thức My^2+frac{8x^2+y}{4x}bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z1. Tìm giá trị lớn nhất của biểu thức:Pdfrac{x}{x+1}+dfrac{y}{y+1}+dfrac{z}{z+1}
Đọc tiếp
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện \(x+y\le1\). Chứng minh\(x^2-\frac{3}{4x}-\frac{x}{y}\le\frac{-9}{4}\)
Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+y\(\ge1\)và x>0
Tìm giá trị nhỏ nhất của biểu thức \(M=y^2+\frac{8x^2+y}{4x}\)
bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z=1. Tìm giá trị lớn nhất của biểu thức:\(P=\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
3: \(P=\dfrac{x}{\left(x+y\right)+\left(x+z\right)}+\dfrac{y}{\left(y+z\right)+\left(y+x\right)}+\dfrac{z}{\left(z+x\right)+\left(z+y\right)}\le\dfrac{1}{4}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}\right)+\dfrac{1}{4}\left(\dfrac{y}{y+z}+\dfrac{y}{y+x}\right)+\dfrac{1}{4}\left(\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)=\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = x = \(\dfrac{1}{3}\).
Đúng 1
Bình luận (0)
Cho x,y >0
Tìm min
a) A= (x+9)(y+9)(1/x + 1/y)
b) B= (1+xy)(1/x + 1/y)