6767∈Q;c)−235∉Q
Đọc tiếp
∈Q;
c)−235∉Q
Những câu hỏi liên quan
Khẳng định nào sau đây là đúng?
\(a)0,25 \in \mathbb{Q};b) - \frac{6}{7} \in \mathbb{Q};c) - 235 \notin \mathbb{Q}\)
a) Đúng vì \(0,25{\rm{ }} = \frac{{25}}{{100}} = \frac{1}{4}\) là số hữu tỉ
b) Đúng vì \(\frac{{ - 6}}{7}\) là số hữu tỉ
c) Sai vì \( - 235 = \frac{{ - 235}}{1}\) là số hữu tỉ.
Chú ý: Một số nguyên cũng là một số hữu tỉ.
Vậy các khẳng định đúng là a và b.
Đúng 0
Bình luận (0)
Cho a 1. Khẳng định nào sau đây là khẳng định đúng ? A.
a
−
3
1
a
5
B.
a
2
3
a
1
C.
a...
Đọc tiếp
Cho a > 1. Khẳng định nào sau đây là khẳng định đúng ?
A. a − 3 > 1 a 5
B. a 2 3 a > 1
C. a 1 3 > a
D. 1 a 2016 < 1 a 2017
Cho a>1. Khẳng định nào sau đây là khẳng định đúng ?
Cho
a
0
,
a
≠
1.
Khẳng định nào sau đây là khẳng định đúng? A. Tập giá trị của hàm số
y
log
a
x
là khoảng
−
∞
;
+
∞
.
B. Tập xác định của hàm số
y
a...
Đọc tiếp
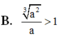
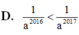
Cho a > 0 , a ≠ 1. Khẳng định nào sau đây là khẳng định đúng?
A. Tập giá trị của hàm số y = log a x là khoảng − ∞ ; + ∞ .
B. Tập xác định của hàm số y = a x là khoảng 0 ; + ∞ .
C. Tập xác định của hàm số y = log a x là khoảng − ∞ ; + ∞ .
D. Tập giá trị của hàm số y = a x là khoảng − ∞ ; + ∞ .
Đáp án A.
Hàm số y = a x có tập giá trị là 0 ; + ∞ ; tập giá trị của hàm số y = log a x là khoảng − ∞ ; + ∞ .
Đúng 0
Bình luận (0)
Cho A là một số nguyên dương. Biết rằng trong ba khẳng định sau đây P, Q, R chỉ có duy nhất một khẳng định sai.
P = “A + 51 là bình phương của một số tự nhiên”
Q = “A có chữ số tận cùng là 1”
R = “A – 38 là bình phương của một số tự nhiên”
Hãy cho biết khẳng định nào là đúng, khẳng định nào là sai? Giải thích.
Giả sử khẳng định Q là đúng A + 51 có tận cùng là 2
P là khẳng định sai (vì không thể là bình phương số tự nhiên)
Khi đó A – 38 có tận cùng là 3 R là khẳng định sai (vì không là bình phương số tự nhiên)
Vậy Q là khẳng định sai và P, R là hai khẳng định đúng.
Đúng 0
Bình luận (0)
Cho A là một số nguyên dương. Biết rằng trong ba khẳng định sau đây P, Q, R chỉ có duy nhất một khẳng định sai.
P = “A + 51 là bình phương của một số tự nhiên”
Q = “A có chữ số tận cùng là 1”
R = “A – 38 là bình phương của một số tự nhiên”
Hãy cho biết khẳng định nào là đúng, khẳng định nào là sai? Giải thích.
Giả sử khẳng định Q là đúng A + 51 có tận cùng là 2
P là khẳng định sai (vì không thể là bình phương số tự nhiên)
Khi đó A – 38 có tận cùng là 3 R là khẳng định sai (vì không là bình phương số tự nhiên)
Vậy Q là khẳng định sai và P, R là hai khẳng định đúng.
Đúng 0
Bình luận (0)
Cho a ; b 0 và
a
2
+
b
2
7
a
b
.
Khẳng định nào sau đây là khẳng định đúng ? A.
2
log
a
+
b
log
a
+
log
b
B.
4
log
a...
Đọc tiếp
Cho a ; b > 0 và a 2 + b 2 = 7 a b . Khẳng định nào sau đây là khẳng định đúng ?
A. 2 log a + b = log a + log b
B. 4 log a + b 6 = log a + log b
C. log a + b 3 = 1 2 log a + log b
D. log a + b 3 = 3 log a + log b
Khẳng định nào sau đây là khẳng định đúng? A. Hai đường thẳng phân biệt không song song thì chéo nhau B. Hai đường thẳng không có điểm chung thì chéo nhau C. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau D. Hai đường thẳng chéo nhau thì không có điểm chung
Đọc tiếp
Khẳng định nào sau đây là khẳng định đúng?
A. Hai đường thẳng phân biệt không song song thì chéo nhau
B. Hai đường thẳng không có điểm chung thì chéo nhau
C. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau
D. Hai đường thẳng chéo nhau thì không có điểm chung
Khẳng định nào sau đây là khẳng định đúng A.
log
3
5
log
7
4
B.
log
1
2
2
0
C.
log
3
π
1
D.
ln
3
log
3
e
Đọc tiếp
Khẳng định nào sau đây là khẳng định đúng
A. log 3 5 > log 7 4
B. log 1 2 2 > 0
C. log 3 π = 1
D. ln 3 < log 3 e