C

C

C

Câu 17: Cho ABC có  AB = AC và  = 2   có dạng đặc biệt nào:

A.  Tam giác cân                               B. Tam giác đều      

C.   Tam giác vuông                          D. Tam giác vuông cân

Câu 18: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Độ dài cạnh BC là:

A. 7cm                     B. 12,5cm                     C. 5cm                  D.

Câu 19: Tam giác ABC có AB = 12cm, AC = 13cm, BC = 5cm. Khi đó vuông tại: 

A. Đỉnh A             B. Đỉnh B             C. Đỉnh C                       D. Tất cả đều sai

Câu 20: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Khẳng định nào sau đây sai?

A.  ABM  = ACM                                   B. ABM= AMC

C.  AMB= AMC= 90⁰                             D. AM là tia phân giác CBA

Câu 22: Cho ABC= DEF. Khi đó:                             .

 A. BC = DF                                     B. AC = DF

   C. AB = DF                                   D. góc A = góc E    

Câu 23. Cho PQR= DEF, DF =5cm. Khi đó:

A.   PQ =5cm           B. QR= 5cm            C. PR= 5cm              D.FE= 5cm                           

có b = 60 độ nha

B

 B

B

Chọn A.

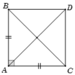
Gọi D  là điểm thỏa mãn tứ giác ADBC là hình vuông.

a) Gọi trung điểm của AC là H. 

Xét tam giác AOH và COH có:

AH = CH (gt)

OH chung

\(\widehat{AHO}=\widehat{CHO}=90^o\)

\(\Rightarrow\Delta AOH=\Delta COH\)  (Hai cạnh góc vuông)

\(\Rightarrow OA=OC\) (Hai cạnh tương ứng)

Hay tam giác OAC cân tại O.

b) Xét tam giác ABO và tam giác AMO có:

AB = AM (gt)

Cạnh AO chung

\(\widehat{BAO}=\widehat{MAO}\)  (Do AO là tia phân giác góc A)

\(\Rightarrow\Delta ABO=\Delta AMO\left(c-g-c\right)\Rightarrow OB=OM\)

Hay tam giác OMB cân tại O.

c) Ta có \(AH=\frac{AC}{2}=\frac{3\sqrt{2}}{2}\left(cm\right)\)

Xét tam giác vuông AOH, áp dụng định lý Pi-ta-go ta có:

\(OH^2=AO^2-AH^2=3^2-\left(\frac{3\sqrt{2}}{2}\right)^2=\frac{9}{2}\)

\(\Rightarrow OH=\frac{3\sqrt{2}}{2}=AH\)

Vậy ta giác OAH vuông cân tại H.  Suy ra  \(\widehat{OAH}=45^o\Rightarrow\widehat{BAC}=2.45^o=90^o\)

Vậy tam giác ABC vuông tại A.

a) Ta có: \(AD=DC=\dfrac{AC}{2}\)(D là trung điểm của AC)

\(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)

mà AC=AB(ΔBAC cân tại A)

nên AD=DC=AE=EB

Xét ΔADE có AE=AD(cmt)

nên ΔADE cân tại A(Định nghĩa tam giác cân)

b) Xét ΔADB và ΔAEC có

AB=AC(ΔABC cân tại A)

\(\widehat{BAD}\) chung

AD=AE(cmt)

Do đó: ΔADB=ΔAEC(c-g-c)

c) Ta có: ΔAED cân tại A(gt)

nên \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAED cân tại A)(1)

Ta có: ΔABC cân tại A(gt)

nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)

Từ (1) và (2) suy ra \(\widehat{AED}=\widehat{ABC}\)

mà hai góc này là hai góc ở vị trí đồng vị

nên ED//BC(Dấu hiệu nhận biết hai đường thẳng song song)

Xét tứ giác BCDE có ED//BC(cmt)

nên BCDE là hình thang có hai đáy là ED và BC(Định nghĩa hình thang)

Hình thang BCDE(ED//BC) có BD=EC(ΔADB=ΔAEC)

nên BCDE là hình thang cân(Dấu hiệu nhận biết hình thang cân)

b) Xét ΔBAH vuông tại H và ΔCAH vuông tại H có 

BA=CA(ΔBAC cân tại A)

AH chung

Do đó: ΔBAH=ΔCAH(cạnh huyền-cạnh góc vuông)

Suy ra: BH=CH(hai cạnh tương ứng)

Xét ΔDHB vuông tại D và ΔEHC vuông tại E có 

HB=HC(cmt)

\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)

Do đó: ΔDHB=ΔEHC(Cạnh huyền-góc nhọn)

Suy ra: HD=HE(Hai cạnh tương ứng)

Xét ΔHDE có HD=HE(cmt)

nên ΔHDE cân tại H(Định nghĩa tam giác cân)

câu a đâu rồi bạn ơi ???