Đó là đường tròn có tâm là trung điểm của AC

a/ Nối AM

- Do D đối xứng với M qua AB => AB là đường trung trực của MD
=> AD=AM (t/c đường trung trực)

- Do E đối xứng với M qua AC => AC là đường trung trực của ME
=> AE=AM (t/c đường trung trực)

Từ đó suy ra: AD=AE hay A là trung điểm của DE hay D đối xứng với E qua A (đpcm)

b/ Ta có: AM=AE (cmt)

- Tứ giác MAEC có: AE=AM => Tứ giác MAEC là hình thoi => CE // AM 

Tương tự ta cũng có: AM=AD (cmt)

- Tứ giác ADBM có: AM=AD => Tứ giác ADBM là hình thoi => BD // AM

Từ đó suy ra được: BD // CE (đpcm)

c/ Điểm M phải là trung điểm của BC thì DE mới có độ dài nhỏ nhất

Đáp án:

Giải thích các bước giải:
a)Do tam giác ABC vuông tại B mà AB=8cm;BC=6cmAB=8cm;BC=6cm

=> theo Pitago ta có: AC=AB2+BC2−−−−−−−−−−√=10AC=AB2+BC2=10

Gọi H là trung điểm của BD => B đối xứng D qua H

Xét tam giác CHBCHB và tam giác CHDCHD có:

HB=HDHB=HD (gt)

góc CHBCHB = góc CHDCHD

CHCH: chung

=> tam giác CHB = tam giác CHD (c.g.c ) => CB=CD=6CB=CD=6

Hoàn toàn tương tự ta có :

tam giác AHBAHB = tam giác AHDAHD (c.g.c) => AB=AD=8AB=AD=8

Xét tam giác ADC có AD=8;CD=6;AC=10AD=8;CD=6;AC=10

=> Theo Định lý Pitago đảo ta có:

=> AD2+CD2=AC2AD2+CD2=AC2

=> Tam giác ADC vuông tại D

=> Xét tứ giác ABCD có:

góc ABCABC = góc ADCADC = 90o90o

=> góc ABCABC +góc ADCADC =180o180o

=> tứ giác ABCD là tứ giác nội tiếp

=> A,B,C,D cùg thuộc đường tròn (ABC) (Đpcm)

b)Do ABC là tam giác vuông; A, B, C cùng thuộc đường tròn => AC là đường kính

Lấy O là tâm đường tròn => O là trung điểm AC

Bán kính đường tròn: OA=OB=AC2=5(cm)

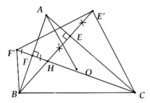
a, ∆CHE' cân tại C =>  C E ' H ^ = C H E ' ^

DBHF' cân tại B =>  B F ' H ^ = B H F ' ^

Mà =>  C H E ' ^ = B H F ' ^  (đối đỉnh)

=>  C E ' H ^ = B F ' H ^

=> Tứ giác BCE'F'  nội tiếp đường tròn tâm (O)

b, Có  B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^

Vậy A, F', E' cùng chắn BC dưới góc bằng nhau

=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)

c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'

=> AO ^ FE

d,  A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC

=> OI = 1 2 AH, BC cố định => OI không đổi

=> Độ dài AH không đổi

=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi

a: D đối xứng B qua AC

=>AC là trung trực của BD

=>AB=AD và CB=CD

Xét ΔABC và ΔADC có

AB=AD

BC=DC

AC chung

Do đó; ΔABC=ΔADC

=>góc ABC=góc ADC=90 độ

Xét tứ giác ABCD có

góc ABC+góc ADC=90 độ+90 độ=180 độ

=>ABCD nội tiếp đường tròn đường kính AC

b: ΔABC vuông tại B

=>AC^2=AB^2+BC^2

=>AC^2=8^2+6^2=10^2

=>AC=8cm

=>R=8/2=4cm