Thay x=-8 và y=6 cào C ta được:

\(C=\dfrac{\left(-8\right)^3}{2}+\dfrac{\left(-8\right)^2.6}{4}+\dfrac{\left(-8\right).6^2}{6}+\dfrac{6^3}{27}\)\(=\dfrac{-512}{2}+\dfrac{384}{4}-\dfrac{288}{6}+\dfrac{216}{27}\)\(=-256+96-48+8=-200\)

\(C=x^2\left(\dfrac{x}{2}+\dfrac{y}{4}\right)+y^2\left(\dfrac{x}{6}+\dfrac{y}{27}\right)=\left(-8\right)^2\left(-\dfrac{8}{2}+\dfrac{6}{4}\right)+6^2\left(-\dfrac{8}{6}+\dfrac{6}{27}\right)=-200\)

a: A=(-x)^3+3*(-x)^2*2+3*(-x)*2^2+2^3=(-x+2)^3

=(28+2)^3=30^3=27000

b: \(C=\left(x+2y-2\right)^3=\left(20+2\cdot9-2\right)^3\)

=36^3

c: 11^3-1

=(11-1)(11^2+11+1)

=10*(121+12)

=1330

d: x^3-y^3=(x-y)^3+3xy(x-y)

=6^3+3*6*9

=216+162

=378

\(\dfrac{1}{3}x^8+\dfrac{1}{4}x^2y+\dfrac{1}{6}xy^2+\dfrac{1}{27}y^3\)

\(=\left(\dfrac{1}{2}x\right)^3+3\cdot\left(\dfrac{1}{2}x\right)^2\cdot\dfrac{1}{3}y+3\cdot\dfrac{1}{2}x\cdot\dfrac{1}{9}y^2+\left(\dfrac{1}{3}y\right)^3\)

\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)

\(=\left(-4+2\right)^3=-8\)

\(A=8x^3+12x^2y+6xy^2+y^3=27\)

\(\Leftrightarrow\left(2x+y\right)^3=27\)

=>2x+y=3

\(B=x\left(2x+y\right)+xy+\dfrac{1}{2}y^2\)

\(=3x+\dfrac{1}{2}y\left(2x+y\right)=3x+\dfrac{1}{2}y\cdot3=3x+\dfrac{3}{2}y\)

\(=\dfrac{3}{2}\left(2x+y\right)=\dfrac{3}{2}\cdot3=\dfrac{9}{2}\)

Lời giải:

Ta có:

\(\frac{9^x}{3^{x+y}}=27\Leftrightarrow \frac{3^{2x}}{3^{x+y}}=27\Leftrightarrow 3^{2x-(x+y)}=27\)

\(\Leftrightarrow 3^{x-y}=27\Leftrightarrow x-y=3\) (1)

Và:

\(\frac{4^{x+y}}{2^{5y}}=64\Leftrightarrow \frac{2^{2x+2y}}{2^{5y}}=64\)

\(\Leftrightarrow 2^{2x+2y-5y}=64\Leftrightarrow 2^{2x-3y}=64\Leftrightarrow 2x-3y=6\) (2)

Từ \((1);(2)\Rightarrow x=3;y=0\)

Khi đó: \(P=2xy-|2y-x|+10=0-|-3|+10=7\)

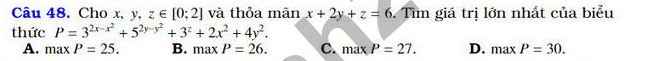
Do \(x;y\in\left[0;2\right]\Rightarrow\left\{{}\begin{matrix}x\left(2-x\right)\ge0\\y\left(2-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow2x^2+4y^2\le4x+8y\)

\(P\le3^0+5^0+3^z+4\left(x+2y\right)=2+3^z+4\left(6-z\right)=3^z-4z+26\)

Xét hàm \(f\left(z\right)=3^z-4z+26\) trên \(\left[0;2\right]\)

\(f'\left(z\right)=3^z.ln3-4=0\Rightarrow z=log_3\left(\dfrac{4}{ln3}\right)=a\)

\(f\left(0\right)=27\) ; \(f\left(2\right)=27\); \(f\left(a\right)\approx-1,1\)

\(\Rightarrow f\left(z\right)\le27\Rightarrow maxP=27\)

(Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;2;2\right)\))

Ồ mà khoan, bài trước bị nhầm lẫn ở chỗ \(3^{2x-x^2}+5^{2y-y^2}\ge3^0+5^0\) mới đúng, ko để ý bị ngược dấu đoạn này

Vậy giải cách khác:

\(0\le x;y;z\le2\Rightarrow x\left(2-x\right)\ge0\Rightarrow2x-x^2\ge0\)

Lại có: \(2x-x^2=1-\left(x-1\right)^2\le1\)

\(\Rightarrow0\le2x-x^2\le1\)

Tương tự ta có: \(0\le2y-y^2\le1\)

Xét hàm: \(f\left(t\right)=3^t-2t\) trên \(\left[0;1\right]\)

\(f'\left(t\right)=3^t.ln3-2=0\Rightarrow t=log_3\left(\dfrac{2}{ln3}\right)=a\)

\(f\left(0\right)=1;\) \(f\left(1\right)=1\) ; \(f\left(a\right)\approx0,73\)

\(\Rightarrow f\left(t\right)\le1\Rightarrow3^t-2t\le1\Rightarrow3^t\le2t+1\)

\(\Rightarrow3^{2x-x^2}\le2\left(2x-x^2\right)+1\)

Hoàn toàn tương tự, ta chứng minh được: 

\(5^t\le4t+1\) với \(t\in\left[0;1\right]\Rightarrow5^{2y-y^2}\le4\left(2y-y^2\right)+1\)

\(3^t\le4t+1\) với \(t\in\left[0;2\right]\Rightarrow3^z\le4z+1\)

\(\Rightarrow P\le2\left(2x-x^2\right)+4\left(2y-y^2\right)+4z+3+2x^2+4y^2=4\left(x+2y+z\right)+3=27\)

Lần này thì ko sai được rồi