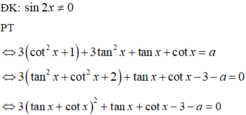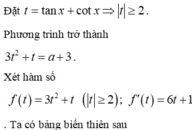Cho biết cotx = 8. Giá trị tanx bằng

Những câu hỏi liên quan
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
a) Hàm số y = tanx nhận giá trị bằng – 1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
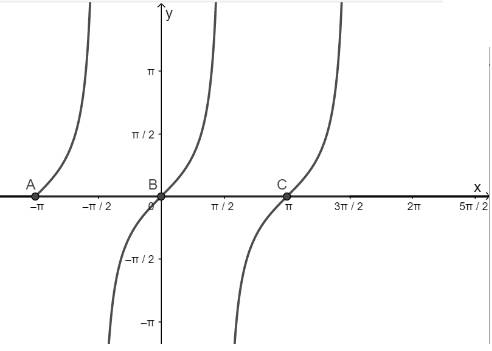
a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
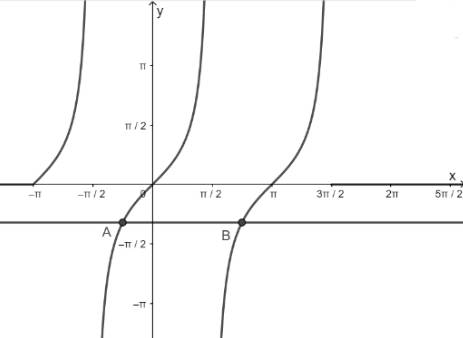
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
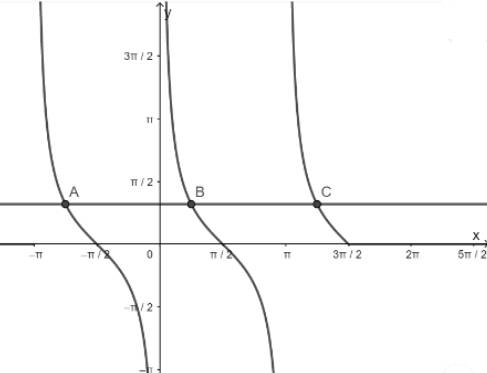
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
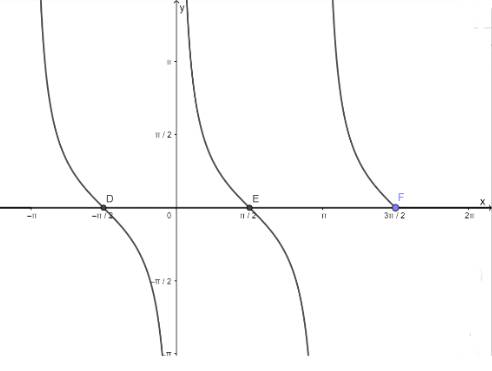
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
tan
x
+
cot
x
. Giá trị
f
π
4
bằng A.
2
B.
2
2
C.0 D.
1
2
Đọc tiếp
Cho hàm số y = f x = tan x + cot x . Giá trị f ' π 4 bằng
A. 2
B. 2 2
C.0
D. 1 2
chọn C
y = tan x + cot x ⇒ y 2 = tan x + cot x ⇒ y ' .2 y = 1 cos 2 x − 1 sin 2 x
⇒ y ' = 1 2 tan x + cot x 1 cos 2 x − 1 sin 2 x
f ' π 4 = 1 2 tan π 4 + cot π 4 1 cos 2 π 4 − 1 sin 2 π 4 = 1 2 2 2 − 2 = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
tan
x
+
cot
x
. Giá trị
f
π
4
bằng A.
2
B. 0 C.
2
2
D.1
Đọc tiếp
Cho hàm số y = f ( x ) = tan x + cot x . Giá trị f ' π 4 bằng
A. 2
B. 0
C. 2 2
D.1
Chọn B
y ' = 1 2 tan x + cot x . ( tan x + cot x ) ' = 1 2 tan x + cot x . 1 cos 2 x − 1 sin 2 x ⇒ y ' π 4 = 1 2 1 + 1 . 1 1 2 − 1 1 2 = 0
Đúng 0
Bình luận (0)
Cho
tan
x
-
tan
y
10
v
à
c
o
t
x
-
c
o
t
y
5
. Giá trị của
tan
x
-
y
là A. 10 B. -10 C.
-
1
10
...
Đọc tiếp
Cho tan x - tan y = 10 v à c o t x - c o t y = 5 . Giá trị của tan x - y là
A. 10
B. -10
C. - 1 10
D. 1 10
Chọn B.

Kết hợp với tan x - tan y = 10 thì ta được tan x . tan y = - 2 .
Do đó
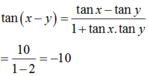
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
A= tanx + cotx +2/tanx +cotx
Từ phương trình 2 (sinx + cosx)= tanx + cotx, ta tìm được cosx có giá trị bằng
A. 1
B. 2
C. 3
D. 4
Chọn C
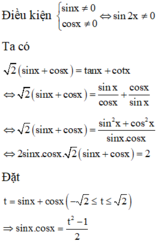
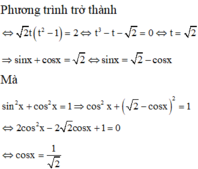
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đầu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:
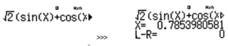
Tiếp theo ta tính cos x thì dễ thấy được:

Đến đây ta dễ dàng chọn được phương án C là phương án đúng thay cho lời giải tự luận nhiều phức tạp.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
sin
x
+
cos
x
+
tan
x
+
c
o
t
x
+
1...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = sin x + cos x + tan x + c o t x + 1 sin x + 1 cos x
A. 2 2 - 1
B. 2 + 1
C. 2 2 + 1
D. 2 - 1
Đáp án A
Phương pháp: Đặt sinx = a, cosx = b
Cách giải: Đặt sinx = a, cosx = b ta có a2 + b2 = 1
Khi đó 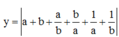
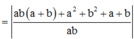
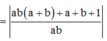
Đặt 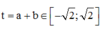
![]()
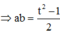
khi đó ta có : 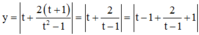
Nếu 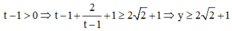
Nếu ![]()
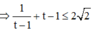
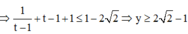
Vậy ![]()
Dấu bằng xảy ra ![]()
![]()
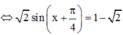
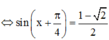
Đúng 0
Bình luận (0)
Tìm giá trọ nhỏ nhất của biểu thức
C= tanx + cotx + 2/(tanx + cotx ?
Có bao nhiêu giá trị nguyên của nhỏ hơn 2018 để phương trình
3
sin
2
x
+
3
tan
2
x
+
tan
x
+
c
o
t
x
α
có nghiệm? A. 2017. B. 3. C. 2010. D. 2011
Đọc tiếp
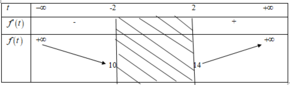
Có bao nhiêu giá trị nguyên của nhỏ hơn 2018 để phương trình 3 sin 2 x + 3 tan 2 x + tan x + c o t x = α có nghiệm?
A. 2017.
B. 3.
C. 2010.
D. 2011