a: \(AH=4\sqrt{3}\left(cm\right)\)

HC=12cm

BC=16cm

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=8\left(cm\right)\\AC=6\left(cm\right)\\AH=4,8\left(cm\right)\end{matrix}\right.\)

b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\cdot6}{2}=24\left(cm^2\right)\)

a, Ta có \(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{3}{5}\approx\sin37^0\Leftrightarrow\widehat{C}\approx37^0\)

\(\Leftrightarrow\widehat{B}=90^0-\widehat{C}=53^0\)

b, Sửa đề: Hãy giải AD,DC

Vì BD là p/g nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow AD=\dfrac{3}{5}DC\)

Mà \(AC=\sqrt{BC^2-AB^2}=4\left(cm\right)\left(pytago\right)\)

Do đó \(\dfrac{3}{5}DC+DC=4\Rightarrow\dfrac{8}{5}DC=4\Rightarrow DC=\dfrac{5}{2}\left(cm\right)\)

\(\Rightarrow AD=\dfrac{3}{2}\left(cm\right)\)

a.     + CH = 10 - 3.6 = 6.4 (cm)

     - Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào ΔABC ta có :

         + \(AH^2=BH.CH\)

      \(\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4.8\) (cm)

         + \(AB^2=BC.BH\)

      \(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{10.3,6}=6\) (cm)

       + \(AC^2=BC.CH\)

      \(\Rightarrow AC=\sqrt{BC.CH}=\sqrt{10.6,4}=8\) (cm)

b.       \(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)

c.       \(P_{ABC}=AB+AC+BC=6+8+10=24\left(cm\right)\)

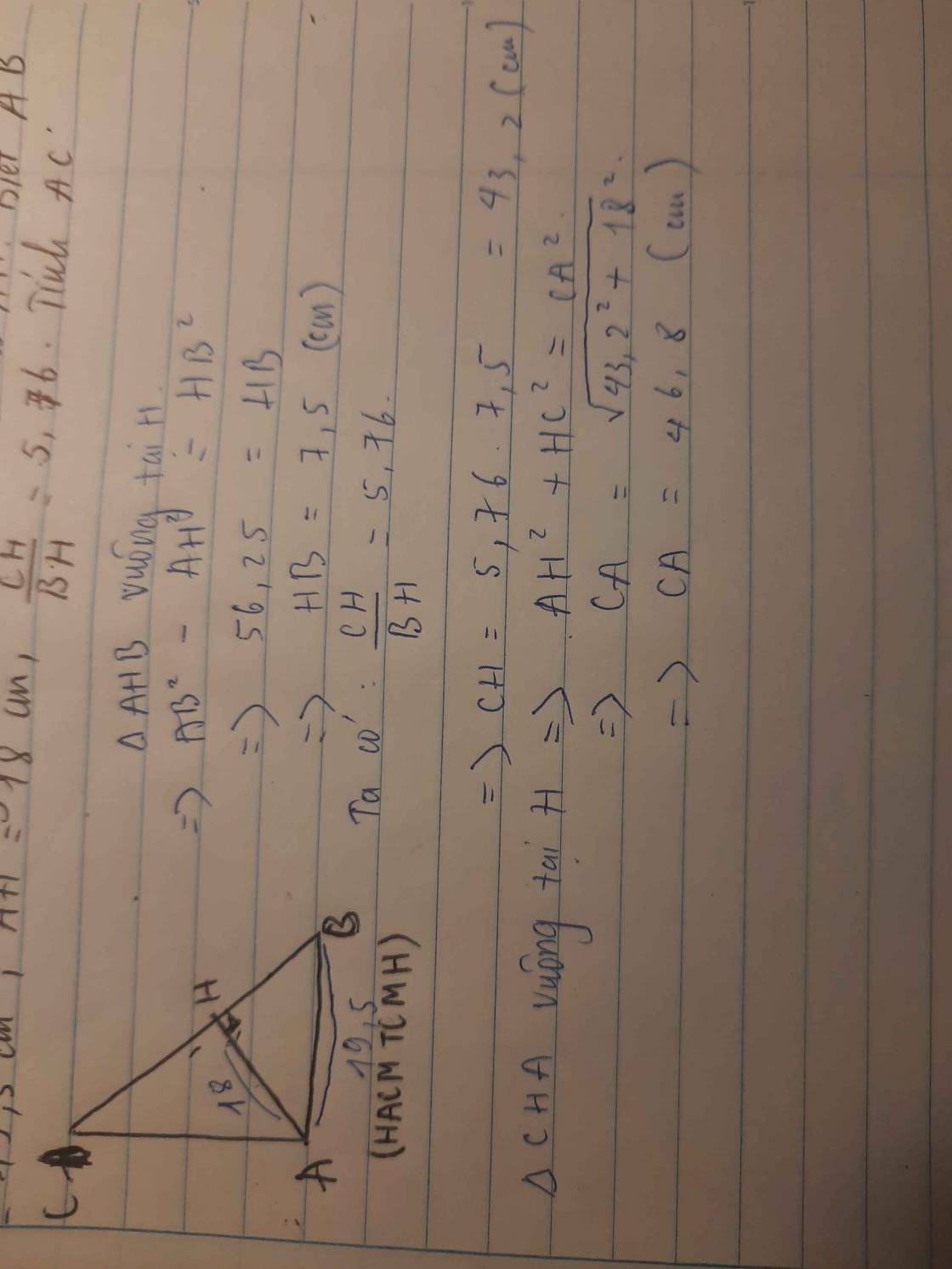  BC=BH+CH

       =7,5+43,2

       =50,7

CVabc= 50.7+19.5+46.8

AH=căn 12^2-9^2=3*căn 7(cm)

CH=AH^2/HB=9*7/9=7(cm)

BC=9+7=16cm

AC=căn CH*BC=4*căn 7(cm)

Xét tam giác \(ABH\) vuông tại H có

\(AH^2+HB^2=AB^2\left(Pytago\right)\)

\(\Leftrightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)

Xét tam giác ABC vuông tại A

\(AB^2=HB.BC\\ \Rightarrow BC=\dfrac{AB^2}{HB}=\dfrac{15^2}{9}=25\left(cm\right)\\ HB+HC=BC\\ \Rightarrow HC=BC-BH=25-9=16\left(cm\right)\\ AB.AC=AH.BC\\ \Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{12.25}{15}=20\left(cm\right)\)

Ta có tam giác ABC vuông tại A và đường cao AH nên:

Áp dụng tính chất cạnh góc vuông và hình chiếu:

\(AB^2=BC\cdot HB\Rightarrow BC=\dfrac{AB^2}{HB}=\dfrac{15^2}{9}=25\left(cm\right)\)

Ta có tam giác HAB vuông tại H áp dụng tính định lý Py-ta-go:

\(AH=\sqrt{AB^2-HB^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)

Mà: \(HB+HC=BC\Rightarrow HC=BC-HB=25-9=16\left(cm\right)\)

Lại áp dụng tính chất hình chiếu và cạnh góc vuông ta có:

\(AC=\sqrt{25\cdot16}=20\left(cm\right)\)

Ta có: \(AC^2=CH\cdot BC\)

\(\Leftrightarrow CH^2+16HC-225=0\)

\(\Leftrightarrow CH^2+25HC-9HC-225=0\)

\(\Leftrightarrow CH=9\left(cm\right)\)

Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:

\(AC^2=AH^2+HC^2\)

\(\Leftrightarrow AH^2=15^2-9^2=144\)

hay AH=12cm

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+HB^2\)

\(\Leftrightarrow AB^2=12^2+16^2=400\)

hay AB=20cm

Ta có: BC=BH+HC

nên BC=9+16=25cm