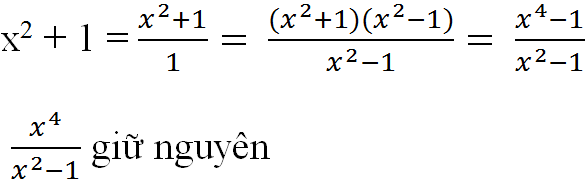Quy đồng mẫu thức các phân thức sau: a) 1/x^2y và 3/xy b) x/(x^2+2xy+y^2) và 2x/(x^2+xy)

Những câu hỏi liên quan
Quy đồng mẫu thức các phân thức sau 1/3x+xy, 2y+2x và 1/x^2+2xy+y^2
\(\dfrac{1}{3x+xy}=\dfrac{1}{x\left(y+3\right)}=\dfrac{\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(2x+2y=2\left(x+y\right)=\dfrac{2\left(x+y\right)\cdot x\left(y+3\right)\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{3x+xy}{x\left(y+3\right)\left(x+y\right)^2}\)
Đúng 2
Bình luận (0)
Bài 2: Rút gọn phân thứcAfrac{10x^2-7+5x-2xy}{1-2x^2+x}Bài 3: Chứng minh rằnga) frac{x^2y+2xy^2+y^3}{2x^2+xy-y^2}frac{xy+y^2}{2x-y}b) frac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}frac{1}{x-y}Bài 4: Quy đồng mẫu thức các phân thức saua) frac{5x}{left(x+3right)^3}&frac{x-4}{3xleft(x+2right)^2}b) frac{x+1}{x-x^2}&frac{x+2}{2x^2+2-4x}
Đọc tiếp
Bài 2: Rút gọn phân thức
\(A=\frac{10x^2-7+5x-2xy}{1-2x^2+x}\)
Bài 3: Chứng minh rằng
a) \(\frac{x^2y+2xy^2+y^3}{2x^2+xy-y^2}=\frac{xy+y^2}{2x-y}\)
b) \(\frac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}=\frac{1}{x-y}\)
Bài 4: Quy đồng mẫu thức các phân thức sau
a) \(\frac{5x}{\left(x+3\right)^3}\&\frac{x-4}{3x\left(x+2\right)^2}\)
b) \(\frac{x+1}{x-x^2}\&\frac{x+2}{2x^2+2-4x}\)
Ta có: \(\frac{x^2y+2xy^2+y^3}{2x^2+xy-y^2}\)
\(=\frac{x^2y+xy^2+xy^2+y^3}{2x^2+2xy-xy-y^2}\)
\(=\frac{xy\left(x+y\right)+y^2\left(x+y\right)}{2x\left(x+y\right)-y\left(x+y\right)}\)
\(=\frac{\left(x+y\right)\left(xy+y^2\right)}{\left(2x-y\right)\left(x+y\right)}=\frac{xy+y^2}{2x-y}\left(đpcm\right)\)
Ta có: \(\frac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}\)
\(=\frac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}\)
\(=\frac{x\left(x+y\right)+2y\left(x+y\right)}{\left(x^2-y^2\right)\left(x+2y\right)}\)
\(=\frac{\left(x+2y\right)\left(x+y\right)}{\left(x+y\right)\left(x-y\right)\left(x+2y\right)}=\frac{1}{x-y}\left(đpcm\right)\)
quy đồng mẫu thức các phân thức sau 1/3x+3y, 1/2y+2x và 1/x^2+2xy+y^2
\(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{2\cdot\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{2x+2y}=\dfrac{1}{2\left(x+y\right)}=\dfrac{3\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{1}{\left(x+y\right)^2}=\dfrac{6}{6\left(x+y\right)^2}\)
Đúng 0
Bình luận (1)
quy đồng các mẫu thức sau
a 1 / x3-8 và 3 / 4-2x
b x / x2-1 và 1 / x2+2x+1
c 1 / x+2 ; x+1 / x2-4x-4 và 5 / 2-x
d 1 / 3x+3y;2x / x2-y2 và x2-xy+y2 / x2-2xy+y2
a) \(\dfrac{1}{x^3-8}=\dfrac{1}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{2}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
\(\dfrac{3}{4-2x}=\dfrac{-3}{2\left(x-2\right)}=\dfrac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
b) \(\dfrac{x}{x^2-1}=\dfrac{x}{\left(x+1\right)\left(x-1\right)}=\dfrac{x\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\)
\(\dfrac{1}{x^2+2x+1}=\dfrac{1}{\left(x+1\right)^2}=\dfrac{x-1}{\left(x+1\right)^2\left(x-1\right)}\)
c) \(\dfrac{1}{x+2}=\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{1}{x^2-4x+4}=\dfrac{1}{\left(x-2\right)^2}=\dfrac{x+2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{5}{2-x}=\dfrac{-5}{x-2}=\dfrac{-5\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)^2}\)
d) \(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{2x}{x^2-y^2}=\dfrac{2x}{\left(x+y\right)\left(x-y\right)}=\dfrac{6x\left(x-y\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{x^2-xy+y^2}{x^2-2xy+y^2}=\dfrac{x^2-xy+y^2}{\left(x-y\right)^2}=\dfrac{3\left(x^2-xy+y^2\right)\left(x+y\right)}{3\left(x+y\right)\left(x-y\right)^2}=\dfrac{3\left(x^3+y^3\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
Đúng 0
Bình luận (2)
tính giá trị các biểu thức sau: A=x^2+xy+y^2/2x^2y+2xy^2 với x+y=3/4 và xy=1/8
Bài 1: Phân tích đa thức sau :
a)2x(xy+y^2-3)
b)(x-y)(2x+y)
c)(x-2y)^2
d)(2x-y)(y+2x)
bài 2: Phân tích các đơn thức thành nhân tử
a)3x^2-3xy
b)x^2-4y^2
c)3x-3y+xy-y^2
d)x^2-1+2y-y^2
Bài 3: Tìm x biết:
a)3x^2-6x=0
b)Tìm x,y thuộc z biết: x^2+4y^2-2xy=4
Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)
Đúng 2
Bình luận (0)
Bài 1 : Phân tích các đa thức sau thành nhân tử :
a) \(2x-2y-x^2+2xy-y^2\)
b) \(x^3-x+3x^2y+3xy^2+y^3-y\)
c) \(x^3-xy^2+x^2y-y^2z\)
a) \(=2\left(x-y\right)-\left(x^2-2xy+y^2\right)\)
\(=2\left(x-y\right)-\left(x-y\right)^2\)
\(=\left(x-y\right)\left(2-x+y\right)\)
Đúng 1
Bình luận (0)
b) \(x^3-x+3x^2y+3xy^2+y^3-y\)
\(=\left(x^3+y^3\right)+\left(3x^2+3xy^2\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+3xy-1\right)\)
\(=\left(x+y\right)\left(x^2+y^2+2xy-1\right)\)
Đúng 2
Bình luận (0)
Quy đồng mẫu thức các phân thức sau :
a) \(\dfrac{1}{x+2},\dfrac{8}{2x-x^2}\)
b) \(x^2+1,\dfrac{x^4}{x^2-1}\)
c) \(\dfrac{x^2}{x^3-3x^2y+3xy^2-y^3},\dfrac{x}{y^2-xy}\)
Bài giải
a) \(\dfrac{1}{x+2}=\dfrac{x.\left(x-2\right)}{\left(x+2\right)\left(x-2\right).x}=\dfrac{x^2-2x}{x\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{8}{2x-x^2}=\dfrac{8}{x\left(2-x\right)}=-\dfrac{8}{x\left(x-2\right)}=-\dfrac{8.\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}\)
b) \(x^2+1=\dfrac{x^2+1}{1}=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\dfrac{x^4-1}{x^2-1}\)
\(\dfrac{x^4}{x^2-1}\) giữ nguyên.
c) \(\dfrac{x^3}{x^3-3x^2y+3xy^2-y^3}=\dfrac{x^3}{\left(x-y\right)^3}=\dfrac{x^3.y}{\left(x-y\right)^3.y}=\dfrac{x^3y}{y\left(x-y\right)^3}\)
\(\dfrac{x}{y^2-xy}=\dfrac{x}{y.\left(y-x\right)}=-\dfrac{x}{y.\left(x-y\right)}=-\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right).\left(x-y\right)^2}=\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right)^3}\)
Đúng 0
Bình luận (0)
*Phân tích thành nhân tử:
x+2
2x-x2=x(2-x)
*MTC:x(2-x)(x+2)
*NTP:x(2-x);x+2
*Quy đồng
\(\dfrac{1}{x+2}\)=\(\dfrac{1x\left(2-x\right)}{\left(x+2\right)x\left(2-x\right)}=\dfrac{1x\left(2-x\right)}{x\left(2-x\right)\left(x+2\right)}\)
\(\dfrac{8}{x\left(2-x\right)}\)\(\dfrac{8\left(x+2\right)}{x\left(2-x\right)\left(x+2\right)}\)=\(\dfrac{8x+16}{x\left(2-x\right)\left(x+2\right)}\)
Đúng 0
Bình luận (0)
a) rút gọn biểu thức\(\dfrac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}\) rồi tính giá trị của biểu thức tại x=5 và y=3
B) phân tích đa thức 2x-2y-x^2+2xy-y^2
B) Ta có: 2x-2y-x2+2xy-y2
⇔ 2(x-y)-(x2-2xy+y2)
⇔ 2(x-y)-(x-y)2
⇔ (x-y)(2-x+y)
Đúng thì tick nhé
Đúng 0
Bình luận (1)