cho đường tròn O đường kính AB=8cm trên tia OB lấy I sao cho OI=1cm vẽ dây CD vuông góc AB tại I E là điểm đối xứng của A qua I tính đoạn thẳng CD

Những câu hỏi liên quan
Bài3 : Cho đường tròn (O) , đường kính AB6cm . Trên đoạn OB lấy điểm M sao cho MB 1cm . Qua M vẽ dây CD của đường tròn (O) vuông góc với AB .a) Chứng minh: △ABC vuông . Tính CB , CDb) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn O ở Ec) Gọi F là giao điểm của AC và DB . Kẻ FH ⊥ AB tại H . Gọi K là giao điểm của CB và FH d) Chứng minh : Ba điểm H, C, E thẳng hàng .giải cụ thể chi tiết giúp mk vớiiiiiii ạ
Đọc tiếp
Bài3 : Cho đường tròn (O) , đường kính AB=6cm . Trên đoạn OB lấy điểm M sao cho MB = 1cm . Qua M vẽ dây CD của đường tròn (O) vuông góc với AB .
a) Chứng minh: △ABC vuông . Tính CB , CD
b) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn O ở E
c) Gọi F là giao điểm của AC và DB . Kẻ FH ⊥ AB tại H . Gọi K là giao điểm của CB và FH
d) Chứng minh : Ba điểm H, C, E thẳng hàng .
giải cụ thể chi tiết giúp mk vớiiiiiii ạ
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Đúng 0
Bình luận (0)
Cho đường tròn (O;4cm), đường kính AB. Lấy điểm M trên đoạn OB sao cho BM=2cm, qua M vẽ dây CD của đường tròn (O) vuông góc với OB.
a) chứng minh tam giác ACB vuông và tính BC
b) chứng minh OCBD là hình thoi
c) trên tia đối của tia BA lấy điểm E sao cho BE=4cm. Chứng minh EC là tiếp tuyến của (O)
GIẢI GIÚP EM VỚI Ạ, EM ĐANG CẦN GẤP HUHU😢 EM CẢM ƠN NHÌU❤💏
Xem chi tiết
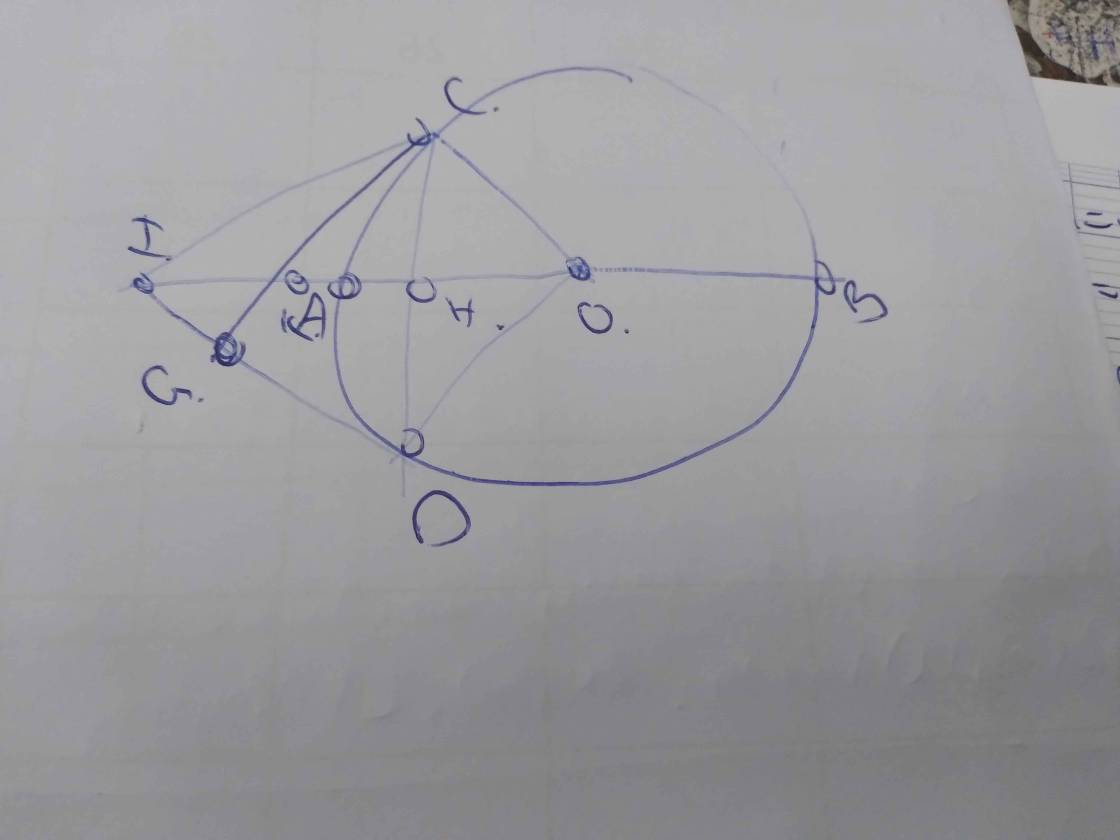
Cho đường tròn tâm O đường kính AB 6cm. Trên đoạn OB lấy điểm M sao cho MB 1cm. Qua M vẽ dây CD của (O) vuông góc với AB.a) C/m: ∆ABC vuông và tính BC?b) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến A của (O) tại E. C/m EC là tiếp tuyến của (O).c) Gọi F là giao điểm của 2 tia AC và DB. Kẻ FH vuông góc AB tại H, K là giao điểm của 2 tia CB và FH. C/m: ∆FBK când) C/m: H, C, E thẳng hàng. Vẽ hình luôn nha các anh/chị. :
Đọc tiếp
Cho đường tròn tâm O đường kính AB = 6cm. Trên đoạn OB lấy điểm M sao cho MB = 1cm. Qua M vẽ dây CD của (O) vuông góc với AB.
a) C/m: ∆ABC vuông và tính BC?
b) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến A của (O) tại E. C/m EC là tiếp tuyến của (O).
c) Gọi F là giao điểm của 2 tia AC và DB. Kẻ FH vuông góc AB tại H, K là giao điểm của 2 tia CB và FH. C/m: ∆FBK cân
d) C/m: H, C, E thẳng hàng.
Vẽ hình luôn nha các anh/chị. :'>
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔCAB vuông tại C có CM là đường cao
nên \(CB^2=BM\cdot BA\)
=>\(CB=\sqrt{1\cdot6}=\sqrt{6}\left(cm\right)\)
b: ΔOAC cân tại O
mà OE là đường cao
nên OE là phân giác của \(\widehat{AOC}\)
Xét ΔOAE và ΔOCE có
OA=OC
\(\widehat{AOE}=\widehat{COE}\)
OE chung
Do đó: ΔOAE=ΔOCE
=>\(\widehat{OCE}=\widehat{OAE}=90^0\)
=>EC là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O; 2,5) đường kính AB. Trên AB lấy điểm H sao cho AH1. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm đối xứng với A qua H.a)Chứng minh tứ giác ACED là hình thoib)Gọi I là giao điểm của DE và BC. Vẽ đường tròn (O) đường kính EB. Chứng minh rằng đường tròn này đi qua I.c)Chứng minh rằng HI là tiếp tuyến của đường tròn (O)d)Tính độ dài HI
Đọc tiếp
Cho đường tròn (O; 2,5) đường kính AB. Trên AB lấy điểm H sao cho AH=1. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm đối xứng với A qua H.
a)Chứng minh tứ giác ACED là hình thoi
b)Gọi I là giao điểm của DE và BC. Vẽ đường tròn (O') đường kính EB. Chứng minh rằng đường tròn này đi qua I.
c)Chứng minh rằng HI là tiếp tuyến của đường tròn (O')
d)Tính độ dài HI

Vẽ hình :
Cho đường tròn ( O ; R ) đường kính AB, dây CD vuông góc với AB tại H ( AH < HB ). Qua C kẻ tiếp tuyến Cx với đường tròn, cắt tia BA tại I. Qua C vẽ tia Cy vuông góc với ID tại G. Gọi K là điểm đối xứng của O qua đoạn CD
Cho đường tròn (O; 15 cm) đường kính AB, lấy điểm I thuộc AO sao cho AI= 5cm. Vẽ dây CD vuông góc với OA tại I. Gọi E là điểm đối xứng vớ A qua I. Các tiếp tuyến với (O) tại C và D cắt nhau tại M.
a/ Tính độ dài CD?
b/ Tứ giác ECAD là hình gì?
c/ chứng minh M,A,B thẳng hàng
Cho đường tròn (O;3cm). Vẽ đường kính AB, lấy điểm M trên AB sao cho AM = 2cm. Qua M vẽ dây CD vuông góc với AB.
a) Tính độ dài đoạn AC
b) Gọi E là điểm đối xứng với A qua điểm M. Tứ giác ACED là hình gì? Vì sao?
c) Vẽ đường tròn tâm O' đường kính EB cắt BC tại K. Tính EK và chứng minh ba điểm D, E, K thẳng hàng
d) Chứng minh MK là tiếp tuyến của đường tròn O'
Bài 4(3 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C bất kỳ trên đường tròn (O; R) (C không trùng A; AC BC). Qua C kẻ dây CD của đường tròn (O; R) vuông góc với đường kính AB tại I. Lấy điểm E sao cho I là trung điểm AE. Tia DE cắt đoạn thẳng BC tại F. Gọi K là trung điểm của BE. 1) Chứng minh tam giác BCD cân. 2) Chứng minh AC I/ DE và chứng minh F thuộc đường tròn tâm K đường kính BE. 3) Chứng minh IF là tiếp tuyến của đường tròn tâm K đường kính BE. 4) Lấy điểm M trên đoạn thẳng O...
Đọc tiếp
Bài 4(3 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C bất kỳ trên đường tròn (O; R) (C không trùng A; AC < BC). Qua C kẻ dây CD của đường tròn (O; R) vuông góc với đường kính AB tại I. Lấy điểm E sao cho I là trung điểm AE. Tia DE cắt đoạn thẳng BC tại F. Gọi K là trung điểm của BE. 1) Chứng minh tam giác BCD cân. 2) Chứng minh AC I/ DE và chứng minh F thuộc đường tròn tâm K đường kính BE. 3) Chứng minh IF là tiếp tuyến của đường tròn tâm K đường kính BE. 4) Lấy điểm M trên đoạn thẳng OC sao cho OM = CI. Chứng minh khi điểm C di chuyển trên nửa đường tròn (O; R) không chứa điểm D (C khác A, B) thì điểm M chạy trên một đường tròn cố định.
Cho đường tròn tâm 0 đường kính AB. Vẽ dãy CD đi qua trung điểm I của
OA và vuông góc với OA.
a) Tính độ dài dây CD biết AB = 20 cm
b) Trên tia đối của tia AO, lấy điểm M sao cho AM = AO. Chứng minh MC là tiếp tuyến của
đường tròn (O).
c) Qua điểm I kẻ dãy EF song song với MC. Gọi H, K lần lượt là chân đường vuông góc kẻ từ
A, B đến EF. Chứng minh EH = FK.
b: Xét ΔMCO có
CA là đường trung tuyến
CA=OM/2
Do đó: ΔMCO vuông tại C
Đúng 1
Bình luận (1)