Không đc dùng tam giác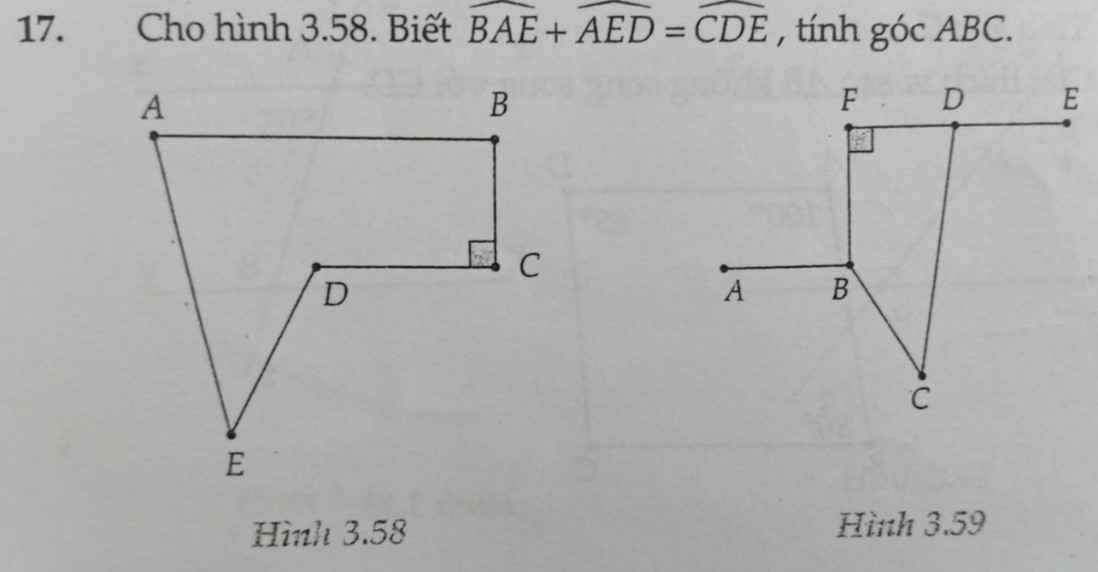

Những câu hỏi liên quan
Không đc dùng tam giác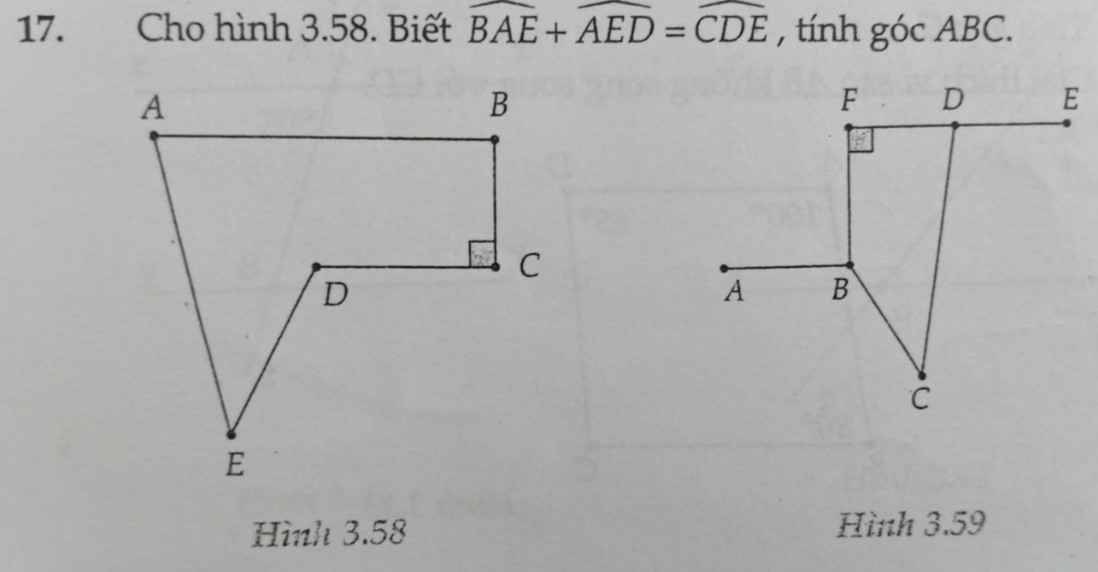
Cái bày này ko chơi tam giác là phức tạp lắm á bạn
Gọi giao của ED với AB là K
góc BAE+góc AED=góc CDE
=>180 độ-góc AKD=góc CDE
=>góc CDE=góc BKD
=>BK//DC
=>góc B=90 độ
Đúng 1
Bình luận (0)
Cho tam giác abc (ab<ac) và đường cao ah.Gọi m,n,p lần lượt là trung điểm của ab,ac và bc.Chứng minh mnph là hình thang cân.
Không đc dùng đường trung bình nhé!!
cho e hỏi là dùng công thức tính diện tích tam giác thường vào tam giác vuông có được không ạ hay là tam giác vuông chỉ dùng được công thức tính diện tích của riêng nó thôi.
Các tam giác đều có công thức tính diện tích giống nhau: \(\dfrac{1}{2}.a.h\)
Đúng 1
Bình luận (0)
Dùng công thức tính diện tích tam giác thường vào tam giác vuông được nhé bạn
Đúng 1
Bình luận (0)
Viết chương trình nhập vào độ dài các cạnh của tam giác rồi tình chu vi của tam giác. Kiểm tra xem tam giác đó có phải là tam giác đều không?
Đừng tham khảo đc k ạ ;-;
=V lúc trước làm bài này nhưng quên cách làm rồi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tam giác ABC có phải là tam giác nhọn không? Em hãy dùng công cụ Góc kiểm tra các góc của tam giác để trả lời câu hỏi đó.
Tam giác ABC là tam giác nhọn
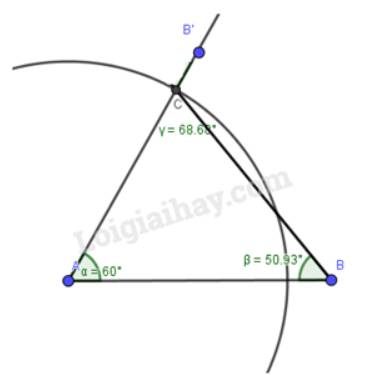
Ta thấy Tam giác ABC có 3 góc đều nhỏ hơn 90 độ nên tam giác ABC là tam giác nhọn
Đúng 0
Bình luận (0)
Em hãy viết câu lệnh hình sau trong Logo, viết bằng 2 cách(cách 1: không dùng thủ tục tam giác ở câu 1, cách 2: dùng thủ tục tam giác ở câu 1) *giúp mình nhé
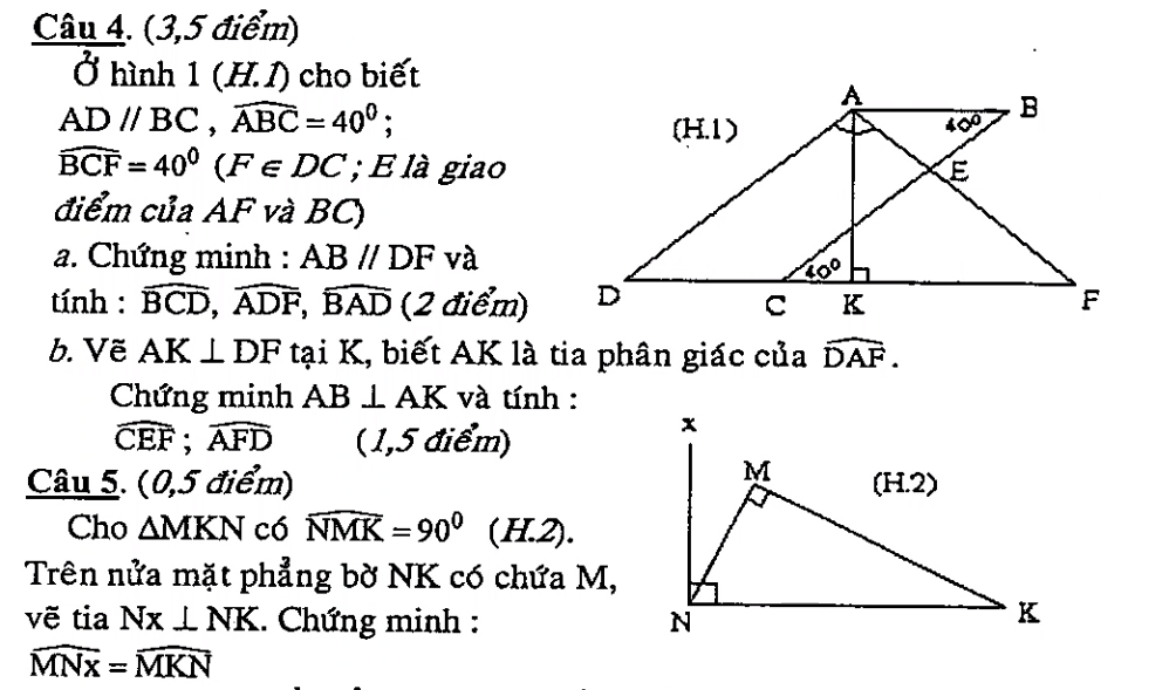
bài 5, không dùng tính chất nào của hình tam giác
a) Em hãy dùng compa kiểm tra xem tam giác nào dưới đây (Hình 4) có 3 cạnh bằng nhau.
b) Với hình tìm được, dùng thước đo góc để kiểm tra các góc của tam giác đó có bằng nhau không?
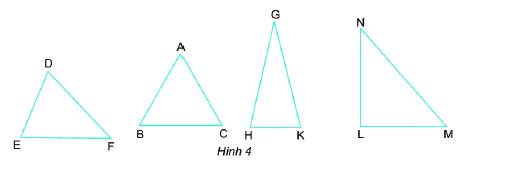
a) Chỉ có ABC là hình có 3 cạnh bằng nhau.
b) Các góc của tam giác ABC bằng nhau và đều bằng \(60^\circ \) .
Đúng 1
Bình luận (0)
Cho tam giác ABC, trên cạnh kéo dài của tam giác ABC lấy AA' = AB, BB'=BC, CC' = AC. Chứng minh trọng tâm tam giác ABC và A'B'C trùng nhau. (không dùng vecto nha).
- Gọi G là trọng tâm \(\Delta ABC\), trung tuyến BE cắt A'C tại E'.
- Gọi trung điểm B'C' là D'. BE và D'C là đường trung bình của \(\Delta CAB'\)và \(\Delta C'AB'\)
=> BE // D'C và BE = D'C
Trung tuyến AD là đường trung bình của \(\Delta BCA'\Rightarrow GE'=BG=\frac{2}{3}\cdot BE=\frac{2}{3}\cdot D'C\)
Gọi G' là giao của A'D' và BE' ta có:
Áp dụng định lí Talet:
\(\frac{G'E'}{D'C}=\frac{A'E'}{A'C}=\frac{AG}{AD}=\frac{2}{3}\) (AD // A'C do là đường trung bình của \(\Delta BA'C\))
\(\Rightarrow G'E'=\frac{2}{3}\cdot D'C\)
=> G'E' = GE'.
Do G và G' cùng nằm trên BE' và G, G' nằm cùng phía so với E' nên G và G' trùng nhau.
Như vậy trung tuyến A'D' đi qua G, tương tự trung tuyến B'M' cũng đi qua G
=> G là trọng tâm của \(\Delta A'B'C'\)
"Nếu G là trọng tâm \(\Delta ABC\) thì vtGA + vtGB + vtGC = vt0"
Gọi giao của AG và BC là D. Trên AD kéo dài lấy E sao cho
DE = DG => GE = GA => vtGE = - vtGA.
Do GE và BC cắt nhau tại trung điểm D của chúng nên BGCE là hình bình hành
=> vtGB + vtGC = vtGE = -vtGA => vtGA + vtGB + vtGC = vt0
Gọi G là trọng tâm ABC, G' là trọng tâm \(\Delta A'B'C'\)
=> vtGA + vtGB + vtGC = vt0, vtG'A' + vtG'B' + vtG'C' = vt0
=> vt0 = (vtG'G + vtGA + vtAA') + (vtG'G + vtGB + vtBB') + (vtG'G + vtGC + vtCC')
=3vtG'G + (vtGA + vtGB + vtGC) + (vtBA + vtCB + vtAC)
=3vtG'G + vt0 + (vtBA + vtAC + vtCB) = 3vtG'G + vt0
=> vtG'G = vt0
=> G' trùng với G
Đúng 0
Bình luận (0)




















