giúp mình 2 câu này với, mình cần gấp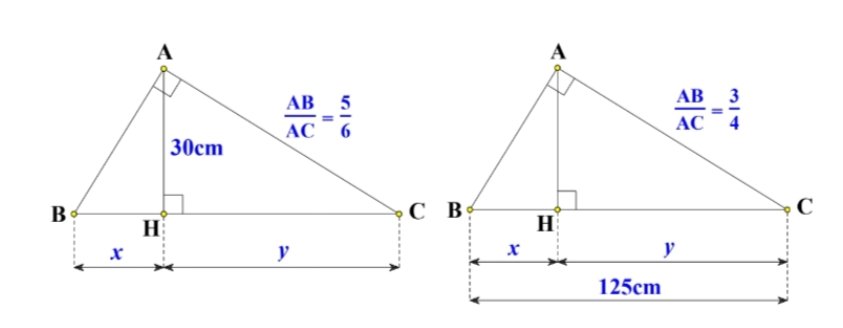

Những câu hỏi liên quan

giúp mình 2 câu này với mình đang cần gấp!!!
Giúp mình 2 câu này với, mình đang cần gấp ạ
c: Ta có: \(\dfrac{1}{x^2+x+1}-\dfrac{1}{x-x^2}+\dfrac{2x}{1-x^3}\)
\(=\dfrac{1}{x^2+x+1}+\dfrac{1}{x\left(x-1\right)}-\dfrac{2x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2-x+x^2+x+1-2x^2}{x\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{1}{x\left(x-1\right)\left(x^2+x+1\right)}\)
Đúng 1
Bình luận (0)
 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp
a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
giúp mình với ạ, mình đang cần gấp 2 câu này ạ.

Gọi vận tốc ca nô là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{72}{x+3}+\dfrac{54}{x-3}=6\Rightarrow x=21\left(tm\right)\)
Đúng 0
Bình luận (1)
Giúp mình làm 2 câu này với ạ! Mình đang cần gấp! Mình xin cảm ơn trước ạ.
Giúp mình câu này với mình cần gấp
uses crt;
var st:string;
d,i:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do
if (st[i] in ['0'..'9']) then write(st[i]);
readln;
end.
Đúng 0
Bình luận (0)
Giúp mình 2 câu này với ạ, mình cần gấp ạ! Cảm ơn trước ạ 💖
a, Gọi chiều rộng ban đầu là x(m) x>0
Chiều dài ban đầu : x+10(m)
Chiều rộng sau khi được tăng: x+5(m)
Chiều dài sau khi giảm: x+10-2=x+8(m)
Theo bài ra ta có pt
(x+8)(x+5)-x(x+10)=100
Giải ra được x=20(m)
Chiều dài : 20=10=30(m)
Diện tích mảnh vườn:20.30=600(m\(^2\))
b, Gọi vận tốc trung bình của xe mày là x(km/h) x>0
Vận tốc tb của ô tô là : x+6(km/h)
Theo bài ra ta có pt
2x+2(x+6)=140
Giải ra được x=32(km/h)
Vtb của ô tô là 32+6=38(km/h)
Đúng 0
Bình luận (0)
Giúp mình câu này với mình đang cần gấp

Phương trình tương đương
\(\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.,k\in Z\)
Xét họ nghiệm \(x=\dfrac{5\pi}{12}+k\pi,k\in Z\).
Do \(-\dfrac{\pi}{2}< \dfrac{5\pi}{12}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{11\pi}{12}< k\pi< \dfrac{9\pi}{4}\)
⇒ \(-\dfrac{11}{12}< k< \dfrac{9}{4}\). Mà k ∈ Z nên k ∈ {0 ; 1}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp :
S1 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12}\right\}\)
Xét họ nghiệm \(x=-\dfrac{\pi}{4}+k\pi\) với k ∈ Z.
Do \(-\dfrac{\pi}{2}< \dfrac{-\pi}{4}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{\pi}{4}< k\pi< \dfrac{35\pi}{12}\)
nên \(-\dfrac{1}{4}< k< \dfrac{35}{12}\). Mà k ∈ Z nên k∈ {0 ; 1 ; 2}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S2 = \(\left\{-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S = S1 \(\cup\) S2 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12};-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Đúng 0
Bình luận (0)
Giúp mình câu này với mình đang cần gấp
a: \(\widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Ta có: SA\(\perp\)(ABCD)
=>SA\(\perp\)AC
=>ΔSAC vuông tại A
Vì ABCD là hình vuông
nên \(AC=AD\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;\left(ABCD\right)}=60^0\)
b: Ta có: BD\(\perp\)AC
BD\(\perp\)SA
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SD}=\widehat{BSD}\)
Vì ABCD là hình vuông
nên \(AC=BD=a\sqrt{2}\)
ΔSAD vuông tại A
=>\(SA^2+AD^2=SD^2\)
=>\(SD^2=\left(a\sqrt{6}\right)^2+a^2=7a^2\)
=>\(SD=a\sqrt{7}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=a\sqrt{7}\)
Xét ΔSBD có \(cosBSD=\dfrac{SB^2+SD^2-BD^2}{2\cdot SB\cdot SD}\)
\(=\dfrac{7a^2+7a^2-2a^2}{2\cdot a\sqrt{7}\cdot a\sqrt{7}}=\dfrac{6}{7}\)
=>\(sinBSD=\sqrt{1-\left(\dfrac{6}{7}\right)^2}=\dfrac{\sqrt{13}}{7}\)
=>\(\widehat{BSD}\simeq31^0\)
=>\(\widehat{SB;\left(SAC\right)}\simeq31^0\)
Đúng 0
Bình luận (0)

























