Bài 3: Cho a,b,c dương thỏa mãn abc=8. Tính giá trị biểu thức ![]()

Những câu hỏi liên quan
Cho các số dương a,b,c thỏa mãn ab+a+b=3; bc+b+c=8; ca+c+a=15. Tính giá trị biểu thức P=a+b+c.
Cho a;b;c là các số dương thỏa mãn: abc=8.Tìm giá trị nhỏ nhất của biểu thức B=(a+b)(b+c)(c+a)
Áp dụng Bất đẳng thức Cauchy cho 2 số không âm ta được :
\(a+b\ge2\sqrt[2]{ab}\)
\(b+c\ge2\sqrt[2]{bc}\)
\(c+a\ge2\sqrt[2]{ca}\)
Nhân theo vế các bất đẳng thức cùng chiều ta được :
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge\left(2\sqrt[2]{ab}\right)\left(2\sqrt[2]{bc}\right)\left(2\sqrt[2]{ca}\right)\)
\(< =>B\ge8\sqrt[2]{a^3b^3c^3}=8abc\)
Mặt khác theo giả thiết ta có : \(abc=8\)
Khi đó \(B\ge8.8=64\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=c=2\)
Vậy \(Min_B=64\)khi \(a=b=c=2\)
sửa lại cho mình dòng 7 trong căn là mũ 2 nhé , đánh lộn
Cho a, b, c là các số dương thỏa mãn \(\left(1+\frac{a}{b}\right).\left(1+\frac{b}{c}\right).\left(1+\frac{c}{a}\right)=8\)
Tính giá trị biểu thức : \(P=\frac{a^3+b^3+c^3}{abc}\)
Cho a,b,c là các số dương thỏa mãn \(\left(1+\frac{a}{b}\right).\left(1+\frac{b}{c}\right).\left(1+\frac{c}{a}\right)=8\)
Tính giá trị của biểu thức: \(P=\frac{a^3+b^3+c^3}{abc}\)
cho a, b, c là 3 số thực dương, thỏa mãn điều kiện a/b=b/c=c/a hãy tính giá trị của biểu thức B= a2022b2023/c4045
Đặt a/b=b/c=c/a=k
=>a=bk; b=ck; c=ak
=>a=bk; b=ak*k=ak^2; c=ak
=>a=ak^3; b=ak^2; c=ak
=>k=1
=>a=b=c
\(B=\dfrac{a^{2022}\cdot a^{2023}}{a^{4045}}=1\)
Đúng 1
Bình luận (0)
Cho số phức z thỏa mãn
z
+
z
¯
+
2
z
-
z
¯
8
; a, b, c dương. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức
P
z
-
3
-
3...
Đọc tiếp
Cho số phức z thỏa mãn z + z ¯ + 2 z - z ¯ = 8 ; a, b, c dương. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P = z - 3 - 3 i . Tính M + m
A. 10 + 34
B. 5 + 58
C. 10 + 58
D. 2 10
Chọn đáp án B
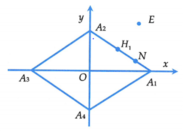
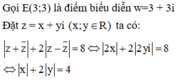
Suy ra điểm N biểu diễn z nằm trên hình bình hành giới hạn bởi các đường thẳng ![]() . Các đỉnh của hình bình hành là
. Các đỉnh của hình bình hành là

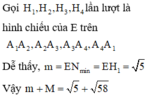

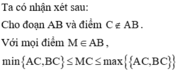


+ Có Hi thuộc đoạn chứa trên di tương ứng thì
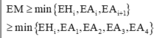
với những Hi thuộc đoạn chứa trên di tương ứng

Đúng 0
Bình luận (0)
cho 3 số dương thỏa mãn a+b+c\(\ge\)6. Tính giá trị nhỏ nhất của biểu thức S=\(a+3b+5c+\frac{1}{a}+\frac{8}{b}+\frac{36}{c}\)
Bài 5:Cho a, b, c là các số dương thảo mãn: \(\left(1+\frac{a}{b}\right).\left(1+\frac{b}{c}\right).\left(1+\frac{c}{a}\right)=8\)
Tính giá trị của biểu thức \(P=\frac{a^3+b^3+c^3}{abc}\)
Cho các số thực dương a,b,c thỏa mãn \(ac\ge12,bc\ge8\). Tìm giá trị nhỏ nhất (nếu có) của biểu thức:
\(D=a+b+c+2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)+\dfrac{8}{abc}\)
Dự đoán điểm rơi xảy ra tại \(\left(a;b;c\right)=\left(3;2;4\right)\)
Đơn giản là kiên nhẫn tính toán và tách biểu thức:
\(D=13\left(\dfrac{a}{18}+\dfrac{c}{24}\right)+13\left(\dfrac{b}{24}+\dfrac{c}{48}\right)+\left(\dfrac{a}{9}+\dfrac{b}{6}+\dfrac{2}{ab}\right)+\left(\dfrac{a}{18}+\dfrac{c}{24}+\dfrac{2}{ac}\right)+\left(\dfrac{b}{8}+\dfrac{c}{16}+\dfrac{2}{bc}\right)+\left(\dfrac{a}{9}+\dfrac{b}{6}+\dfrac{c}{12}+\dfrac{8}{abc}\right)\)
Sau đó Cô-si cho từng ngoặc là được
Đúng 2
Bình luận (1)














