Cho tam giác ABC góc A = 90 do,biết cos B =0,8. Hãy tan B?

Những câu hỏi liên quan
cho tam giác ABC vuông tại A. Biết cos B=0,8. Hãy tính các tỉ số lượng giác của góc C
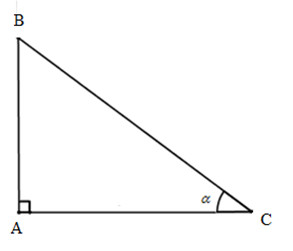
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Ta có:
Sin2C+cos2C=1Sin2C+cos2C=1
⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;⇒cosC=0,6;
tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;
cotgC=cosCsinC=0,60,8=34
Đúng 1
Bình luận (0)
bài 1
cho góc a(0<a<90)hãy tính sin a ,tan a nếu
a)cos a=12/13
b)cos a=3/5
bài 2
cho tam giác abc vuông tại a,đường cao ah,tính tỉ số lượng giác của góc C,từ đó suy ra tỉ số lượng giác của góc B,biết
a,AB=16cm,AC=12cm
b,Ac=13cm,CH=5cm
c,CH=3cm,BH=4cm
a) Ta có: \(cos\alpha=\dfrac{12}{13}\)
Mà: \(sin^2\alpha+cos^2a=1\)
\(\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha=1-\left(\dfrac{12}{13}\right)^2\)
\(\Rightarrow sin^2\alpha=\dfrac{25}{169}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{25}{169}}\)
\(\Rightarrow sin\alpha=\dfrac{5}{13}\)
Mà: \(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{5}{13}}{\dfrac{12}{13}}=\dfrac{5}{12}\)
b) Ta có: \(cos\alpha=\dfrac{3}{5}\)
Mà: \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha=1-\left(\dfrac{3}{5}\right)^2\)
\(\Rightarrow sin^2\alpha=\dfrac{16}{25}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}\)
Mà: \(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{4}{5}}{\dfrac{3}{5}}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
2:
a: BC=căn 16^2+12^2=20cm
Xét ΔABC vuông tại A có
sin B=cos C=AC/BC=3/5
cos B=sin C=AB/BC=4/5
tan B=cot C=3/5:4/5=3/4
cot B=tan C=1:3/4=4/3
b: AH=căn 13^2-5^2=12cm
Xét ΔAHC vuông tại H có
sin C=AH/AC=12/13
=>cos B=12/13
cos C=HC/AC=5/13
=>sin B=5/13
tan C=12/13:5/13=12/5
=>cot B=12/5
tan B=cot C=1:12/5=5/12
c: BC=3+4=7cm
AB=căn BH*BC=2*căn 7(cm)
AC=căn CH*BC=căn 21(cm)
Xét ΔABC vuông tại A có
sin B=cos C=AC/BC=căn 21/7
sin C=cos B=AB/BC=2/căn 7
tan B=cot C=căn 21/7:2/căn 7=1/2*căn 21
cot B=tan C=1/căn 21/2=2/căn 21
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Biết \(\cos B=0,8\), hãy tính các tỉ số lượng giác của góc C
Gợi ý : Sử dụng bài tập 14
Vì hai góc B và C phụ nhau nên sinC=cosB=0,8.
Ta có:
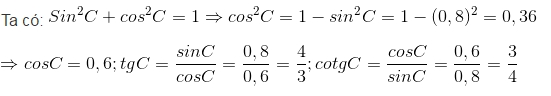
Nhận xét: Nếu biết sinα (hay cosα) thì ta có thể tính được ba tỷ số lượng giác còn lại.
Đúng 0
Bình luận (0)
Hướng dẫn giải:
Vì hai góc B và C phụ nhau nên sinC=cosB=0,8.
Ta có: Sin2C+cos2C=1⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;tgC=sinCcosC=0,80,6=43;cotgC=cosCsinC=0,60,8=34
Nhận xét: Nếu biết sinα (hay cosα) thì ta có thể tính được ba tỷ số lượng giác còn lại.
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a biết sin B=0,8. Tính cos B và cos C
Tìm độ dài cạnh và số đo các góc chưa biết của tam giác ABC trong các trường hợp sau:
a) góc A = 90°,tan B = 5, AC = 5.
b) góc A = 90°, cos B = 3, AB = 3.
c) góc A = 75°, góc B = 60°, BC = 1+\(\sqrt{3}\).
Cho tam giác ABC góc A = 90 do,biết cos B =0,8. Hãy tính tỉ số lượng giác của góc C
cho tam giác ABC có Â = 90 độ,B^ = 50 độ
a) viết các tỉ số lượng giác của B^
b) kẻ đường cao AH, biết sin CÂH=0,8. Tính cos,tan,cot của CÂH
cho tam giác abc có A^=90 độ AB= 6cm và AC = 8cm a/ tính Bc? b/ tính sin B và Tan C? C/ gọi AH là đường cao tam giác ABC , tính cos BAH^,d/ Gọi M là trung điểm Bc từ M kẻ đường thẳng vuông góc với BC cắt AC tại T tính độ dài AT?
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=4cm,AC=9cm. Tính sin B, sin C
2.Cho tam giác ABC vuông tại A, Cos B= an pha, Cos = 4/5. Tính sin, tan,cos
3. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=6cm, BC= 10cm
a. Tính AC,AH. Tỉ số đồng giác góc B,C
b. Gọi E,F lần lượt là hình chiếu H lên AB,AC. CM :AE.AD=AF.AC
c. Tính S tứ giác AEHF




















