\(\left(\dfrac{1}{\sqrt{x}}-\sqrt{x}\right):\left(\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\) (ĐK: \(x>0\))

\(=\left(\dfrac{1}{\sqrt{x}}-\dfrac{x}{\sqrt{x}}\right)\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)

\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{-\sqrt{x}}\cdot\dfrac{-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)

\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{-\sqrt{x}\left(\sqrt{x}-1\right)}\)

\(=\left(\sqrt{x}+1\right)^2\)

c: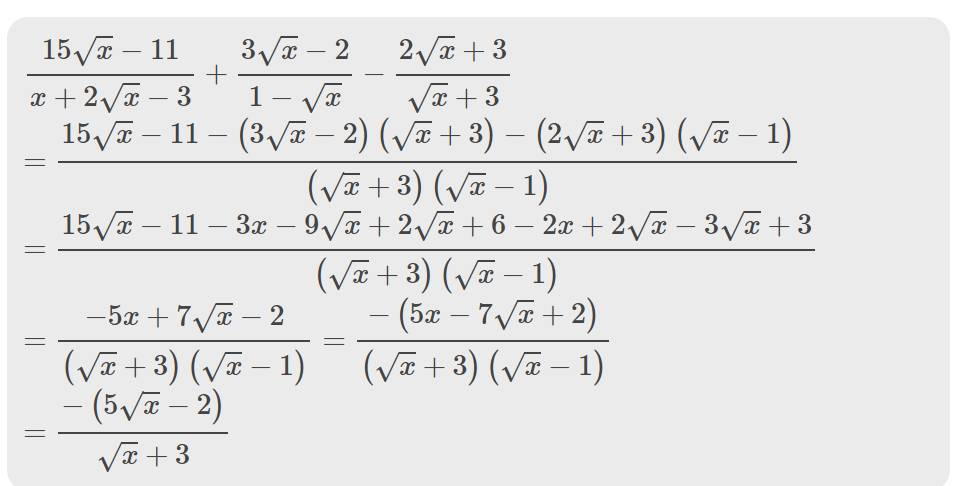 

b; 

Sửa đề: \(\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2\sqrt{x}\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2x-6\sqrt{x}+x-4\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{x\sqrt{x}-x+16\sqrt{x}-16}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{x+16}{\sqrt{x}+3}\)

a, -19 - x = -20

           x = -19 - (-20)

           x = -19 + 20

           x = 1

b, 5x - 6 = 3x + 12

    5x - 6 - 3x = 12

    5x - 3x      = 12 + 6

    (5 - 3)x      = 18

    2x             = 18

    x              = 18 : 2

    x              = 9

c, 15 - 3 (x - 1) = 8 - 2x

    15 - 3 (x - 1) + 2x = 8

          -3x - 3 - 2x = 8 - 15

          -3x - 3 - 2x = -7

          -3x - 2x - 3 = 7

          -3x - 2x       = 7 + 3

           (-3 - 2) x      = 10

                   -5x     = 10

                      x      = 10 : (-5)

                      x      = -2

d, (5x - 6)² = 16

    (5x - 6)² = 4²

=> 5x - 6 = 4

     5x      = 4 + 6

     5x      = 10

       x      = 10 : 5

       x     = 2

f, 26 - | x + 9 | = 13

          | x + 9 | = 26 - 13

=>      | x + 9 | = 13

=>        x + 9 = +- 13

* Với x + 9 = 13

         x      = 13 - 9

         x      = 4

* Với x + 9 = -13

         x      = -13 - 9

         x      = -22

Vậy x = {4;-22}

e, | 3 + x | = 19

=>  3 + x = +- 19

* Với 3 + x = 19

              x = 19 - 3

              x = 16

* Với 3 + x = -19

              x = -19 - 3

              x = -22

Vậy x = {16;-22}

a, X = -19+20=1

b, (5-3)X = 18

       2X   = 18

=>    X    = 9

c, 3X + 3 -2X = 7

         X+3     =7

           X       = 4

f, |X+9| = 13

ta có 2 trường hợp:

TH1: X+9 = 13

=> X= 4

TH2 : X+9 = -13 

=> X= -22

e, ta có 2 trường hợp:

TH1: 3+X = 19

=> X= 16

TH2: 3+X = -19

=> X= -22

ban tu lam di,luoi the

bai ki vay ,

khó à nghen

Yêu cầu đề bài là gì bạn nên ghi đầy đủ để được hỗ trợ tốt hơn.

a) -x + 8 = -17

⇔ -x = -17 - 8

⇔ -x = -25

⇔ x = 25

b) 35 - x = 37

⇔ x = 35 - 37

⇔ x = -2

c) -19 - x = -20

⇔ x = -19 + 20

⇔ x = 1

d) x - 45 = -17

⇔ x = -17 + 45

⇔ x = 28

e) |x + 3| = 15

⇔ \(\left[{}\begin{matrix}x+3=15\\x+3=-15\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=15-3\\x=-15-3\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=12\\x=-18\end{matrix}\right.\)

f) |x - 3| - 16 = -4

⇔ |x - 3| = -4 + 16

⇔ |x - 3| = 12

⇔ \(\left[{}\begin{matrix}x-3=12\\x-3=-12\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=12+3\\x=-12+3\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=15\\x=-9\end{matrix}\right.\)

k) 26 - |x + 9| = -13

⇔ |x + 9| = 26 + 13

⇔ |x + 9| = 39

⇔ \(\left[{}\begin{matrix}x+9=39\\x+9=-39\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=39-9\\x=-39-9\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=30\\x=-48\end{matrix}\right.\)

a,-x + 8 = -17

=> -x=-17-8

=> -x=-25

=> x=25

vậy x=25

b, 35 - x = 37

=> x=35-37

=> x=-2

vậy x=-2

c, -19 -x = -20

=> x=-19+20

=> x=1

vậy x=1

d, x - 45 = -17

=> x=-17+45

=> x=28

vậy x=28

e, | x+ 3| = 15

th1 x+3=15

=> x=15-3

=> x=12

th2 x+3=-15

=> x=-15-3

=> x=-18

vậy x=12 hoặc x=-18

g, |x-7| +13 = 25

=> \(\left|x-7\right|=25-13\)

=> \(\left|x-7\right|=12\)

th1 x-7=12

=> x=12+7

=> x=19

th2 x-7=-12

=>x=-12+7

=> x=-5

vậy x=19 hoặc x=-5

các câu sau tt

g) |x - 7| + 13 = 25

⇔ |x - 7| = 25 - 13

⇔ |x - 7| = 12

⇔ \(\left[{}\begin{matrix}x-7=12\\x-7=-12\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=12+7\\x=-12+7\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x=19\\x=-5\end{matrix}\right.\)

\(A=\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)

\(A=\dfrac{x\sqrt{x}+26\sqrt{x}-19}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)

\(A=\dfrac{x\sqrt{x}+26\sqrt{x}-19}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(A=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2x-6\sqrt{x}+x-3\sqrt{x}-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(A=\dfrac{x\sqrt{x}-x+16\sqrt{x}-16}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(A=\dfrac{\left(x\sqrt{x}-x\right)+\left(16\sqrt{x}-16\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(A=\dfrac{x\left(\sqrt{x}-1\right)+16\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(A=\dfrac{\left(\sqrt{x}-1\right)\left(x+16\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(A=\dfrac{x+16}{\sqrt{x}+3}\)