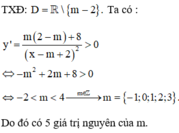a: \(y'=\dfrac{\left(x-1\right)'\left(x+1\right)-\left(x-1\right)\left(x+1\right)'}{\left(x+1\right)^2}\)

\(=\dfrac{x+1-x+1}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}>0\)

=>Hàm số luôn đồng biến khi x<>-1

vậy: Các khoảng đồng biến là \(\left(-\infty;-1\right);\left(-1;+\infty\right)\)

b: \(y'=\dfrac{\left(2x+1\right)'\left(8x-1\right)-\left(2x+1\right)\left(8x-1\right)'}{\left(8x-1\right)^2}\)

\(=\dfrac{2\left(8x-1\right)-8\left(2x+1\right)}{\left(8x-1\right)^2}\)

\(=\dfrac{16x-2-16x-8}{\left(8x-1\right)^2}=-\dfrac{10}{\left(8x-1\right)^2}< 0\)

=>Hàm số nghịch biến khi x<>1/8

Vậy: Các khoảng nghịch biến là \(\left(-\infty;\dfrac{1}{8}\right);\left(\dfrac{1}{8};+\infty\right)\)

\(y'=\dfrac{2x^2-4mx-m^2+2m-1}{\left(x-m\right)^2}\)

Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta có:

\(\left\{{}\begin{matrix}2x^2-4mx-m^2+2m-1\ge0\left(1\right)\\m\le1\end{matrix}\right.\)

Xét (1): ta có \(\Delta'=4m^2-2\left(-m^2+2m-1\right)=6m^2-4m+2>0\) ; \(\forall m\)

\(\Rightarrow\) (1) thỏa mãn khi: \(x_1< x_2\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)\ge0\\\dfrac{x_1+x_2}{2}< 1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1\ge0\\x_1+x_2< 2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-m^2+2m-1}{2}-2m+1\ge0\\2m< 2\end{matrix}\right.\) \(\Rightarrow-1-\sqrt{2}\le m\le-1+\sqrt{2}\)

Bài 1: 

a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)

b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0

hay k>2

Bài 2: 

Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:

\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)

\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)

\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)

\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)

hay \(m=\dfrac{1}{3}\)

\(a,\Leftrightarrow\sqrt{\dfrac{m-2}{m+3}}>0\)

Mà \(\sqrt{\dfrac{m-2}{m+3}}\ge0\Leftrightarrow\sqrt{\dfrac{m-2}{m+3}}\ne0\Leftrightarrow m\ne2;m\ne-3\)

\(b,y=m^2x-5mx-6m=x\left(m^2-5m\right)-6m\)

Đồng biến \(\Leftrightarrow m^2-5m>0\Leftrightarrow m\left(m-5\right)>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>5\end{matrix}\right.\)

\(c,y=x\left(\dfrac{m+5}{m-2}-1\right)+\sqrt{m-2}=\dfrac{7}{m-2}x+\sqrt{m-2}\)

Đồng biến \(\Leftrightarrow\dfrac{7}{m-2}>0\Leftrightarrow m-2>0\Leftrightarrow m>2\)

a: Để hàm số trên là hàm số bậc nhất thì \(\left\{{}\begin{matrix}m\ge0\\m\ne4\end{matrix}\right.\)

b: Để hàm số đồng biến thì \(\sqrt{m}-2>0\)

hay m>4

\(y'=-x^2+2\left(a-1\right)x+a+3\)

Hàm đồng biến trên khoảng đã cho khi với mọi \(x\in\left(0;3\right)\) ta có:

\(-x^2+2\left(a-1\right)x+a+3\ge0\)

\(\Leftrightarrow\left(2x+1\right)a\ge x^2+2x-3\)

\(\Rightarrow a\ge\dfrac{x^2+2x-3}{2x+1}\)

Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) với \(x\in\left(0;3\right)\)

\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến

\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\Rightarrow a\ge\dfrac{12}{7}\)

Đáp án B

Đáp án B

TXĐ:  D = ℝ \ m − 2 .  Ta có:

y ' = m 2 − m + 8 x − m + 2 2 > 0 ⇔ − m 2 + 2 m + 8 > 0

⇔ − 2 < m < 4 → m ∈ ℤ m = − 1 ; 0 ; 1 ; 2 ; 3 .

Do đó có 5 giá trị nguyên của m.

Lời giải:
Đặt $t=\frac{2x}{x^2+1}$

$t+1=\frac{(x+1)^2}{x^2+1}\geq 0\Rightarrow t\geq -1$

$1-t=\frac{(x-1)^2}{x^2+1}\geq 0\Rightarrow t\leq 1$

Vậy $-1\leq t\leq 1$

$y=t^2-4t+25=(t+1)(t-5)+30$

Vì $-1\leq t\leq 1$ nên $t+1\geq 0; t-5\leq 0\Rightarrow (t+1)(t-5)\leq 0$

$\Rightarrow y\leq 30$

Vậy $y_{\max}=30$