cho hình chóp tứ giác đều s abcd có diện tích toàn phần là 465 cm2 và trung đoạn bằng 8 cm . tính diên tích đáy LẸ NHA MN

Những câu hỏi liên quan
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 3cm, trung đoạn bằng 5cm.Tính diện tích xung quanh , diện tích toàn phần và thể tích của hình chóp.
\(S_{xq}=\dfrac{4.8}{2}.5=80\left(cm^2\right)\\ S_{tp}=80+8^2=144\left(cm^2\right)\\ V=\dfrac{1}{3}.8^2.3=64\left(cm^3\right)\)
Đúng 0
Bình luận (0)
cho hình chóp tứ giác đều có cạnh đáy 8cm, trung đoạn bằng 5cm. Tính diện tích xung quanh và diện tích toàn phần ( tổng diện tích các mặt của hình chóp ) của hình tứ giác đều đó ?
Nữa chu vi đáy của hình chóp đều:
\(8\cdot4:2=16\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=16\cdot5=80\left(cm^2\right)\)
Diện tích đáy của hình chóp đều:
\(S_đ=8^2=64\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=64+80=144\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Sxq=1/2*8*4*5=80cm2
Stp=80+8^2=144cm2
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều s . AB CD có độ dài cạnh bên bằng 6 cm độ dài cạnh đáy 4 cm .
a tính độ dài Trung đoạn
b, tính diện tích xung quanh
c ,Tính diện tích toàn phần
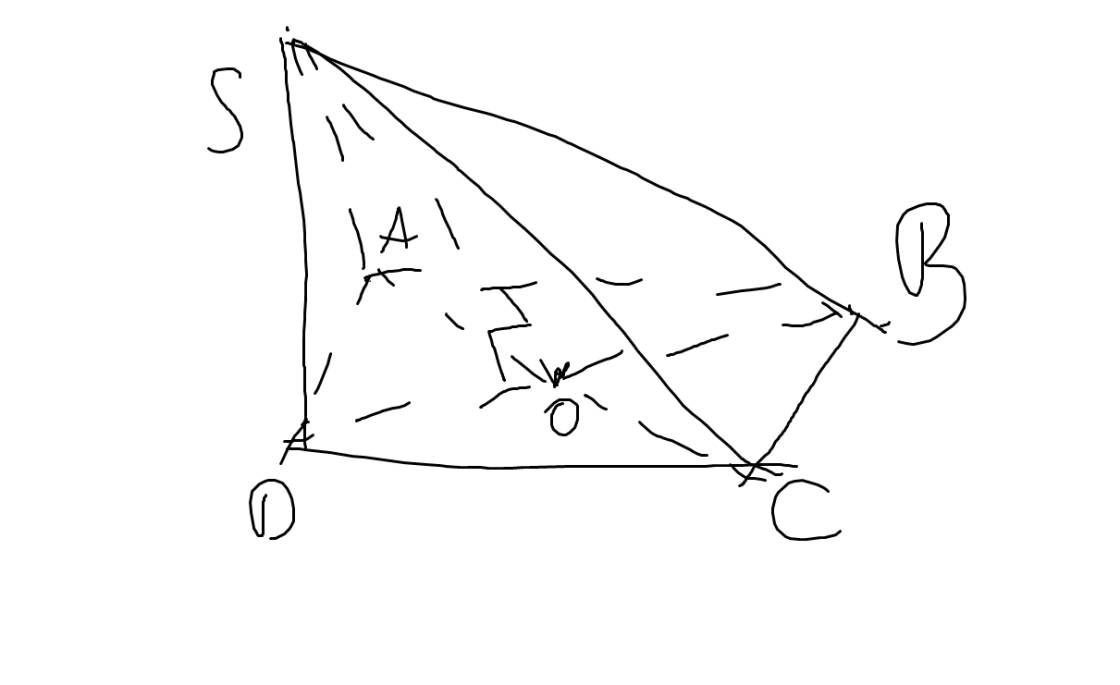
Trong hình chóp tứ giác đều, đường cao kẻ từ đỉnh xuống đáy có chân đường cao là tâm của đáy và đường cao đó chính là trung đoạn của hình chóp
a: Vẽ SO\(\perp\)(ABCD)
=>SO là trung đoạn của hình chóp ABCD và O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
ABCD là hình vuông
=>\(AC=BD=\sqrt{4^2+4^2}=4\sqrt{2}\left(cm\right)\)
=>\(AO=BO=CO=DO=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\left(cm\right)\)
SO vuông góc (ABCD)
=>SO vuông góc OD
=>ΔSOD vuông tại O
=>\(SO^2+OD^2=SD^2\)
=>\(SO^2=6^2-8=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{Xq}=p\cdot d=C_{đáy}\cdot SO=4\cdot4\cdot2\sqrt{7}=32\sqrt{7}\left(cm^2\right)\)
c: \(S_{tp}=S_{xq}+S_{đáy}\)
\(=32\sqrt{7}+4^2=32\sqrt{7}+16\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có AC = SC = 8 cm , SH = 6,93 cm ,S tam giác ABC = 27,72 cm2
a) Cho biết độ dài trung đoạn của hình chóp S.ABC.
b) Tính diện tích xung quanh và diện tích toàn phần của hình chóp S.ABC.
c) Tính thể tích của hình chóp tam giác đều S.ABC biết chiều cao của hình chóp là 7,5 cm
a) Độ dài trung đoạn của hình chóp S.ABC là độ dài đoạn thẳng từ trung điểm của cạnh đáy đến đỉnh của hình chóp. Vì tam giác ABC là tam giác đều, nên ta có thể tính độ dài trung đoạn bằng cách sử dụng công thức Pythagoras: Trung đoạn = căn bậc hai của (AC^2 - (AC/2)^2) = căn bậc hai của (8^2 - (8/2)^2) = căn bậc hai của (64 - 16) = căn bậc hai của 48 = 4 căn 3 cm
b) Diện tích xung quanh của hình chóp S.ABC là tổng diện tích các mặt bên của hình chóp. Vì tam giác ABC là tam giác đều, nên diện tích mặt bên của hình chóp là diện tích tam giác đều. Ta có công thức tính diện tích tam giác đều: Diện tích tam giác đều = (cạnh^2 * căn 3) / 4 = (8^2 * căn 3) / 4 = 16 căn 3 cm^2
Diện tích xung quanh = Diện tích tam giác đều + Diện tích đáy = 16 căn 3 + 27,72 = 16 căn 3 + 27,72 cm^2
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy: Diện tích toàn phần = Diện tích xung quanh + Diện tích đáy = 16 căn 3 + 27,72 + 27,72 = 16 căn 3 + 55,44 cm^2
c) Thể tích của hình chóp tam giác đều S.ABC được tính bằng công thức: Thể tích = (Diện tích đáy * Chiều cao) / 3 = (27,72 * 7,5) / 3 = 69,3 cm^3
Đúng 0
Bình luận (1)
một hình chóp tứ giác đều có chiều cao bằng 15cm, trung đoạn bằng 17cm, độ dài cạnh đáy của hình chóp bằng 16cm. Tính diện tích xung quanh, diện tích toàn phần ( tổng diện tích các mặt đáy của hình chóp ), thể tích của hình chóp tứ giác đều?
Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Đúng 0
Bình luận (0)
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.
+ Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
+ Tính thể tích của hình chóp.
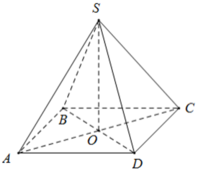
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
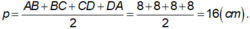

Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.
+ Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
+ Tính thể tích của hình chóp.
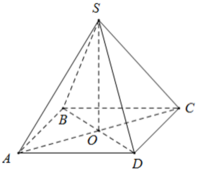
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
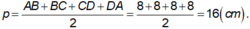

Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.
+ Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
+ Tính thể tích của hình chóp.
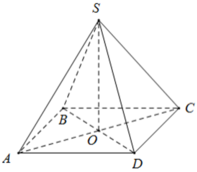
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
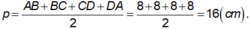

Đúng 1
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.
+ Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
+ Tính thể tích của hình chóp.
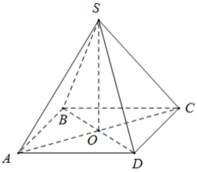
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
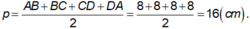
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )
Đúng 0
Bình luận (0)













