 giúp e câu a,b,c vs ạ
giúp e câu a,b,c vs ạ

Những câu hỏi liên quan
giúp e câu a,b,c,e vs ạ
Những câu đã đăng rồi thì em hạn chế đăng lại nhé.
Đúng 1
Bình luận (1)
a: \(=\dfrac{\left(4\sqrt{3}-5\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}\right)}{\sqrt{3}}\)
=4-5+1/2*4
=-1+2
=1
b: \(=\left|2-\sqrt{5}\right|-\left|\sqrt{5}+1\right|\)
\(=\sqrt{5}-2-\sqrt{5}-1=-3\)
c: \(=\dfrac{3\left(\sqrt{7}+2\right)}{3}-\dfrac{4\left(3-\sqrt{7}\right)}{2}\)
\(=\sqrt{7}+2-2\left(3-\sqrt{7}\right)\)
\(=\sqrt{7}+2-6+2\sqrt{7}=3\sqrt{7}-4\)
d: \(=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)
\(=3\sqrt{2a}-3a\cdot\sqrt{2a}+2\sqrt{2a}-2\sqrt{2a}\)
\(=\sqrt{2a}\left(3-3a\right)\)
e: \(=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{2\left(\sqrt{3}+1\right)}{2}\)
\(=\sqrt{3}-\sqrt{3}-1=-1\)
Đúng 0
Bình luận (0)
giúp e câu a,b,c,e vs ạ
a) \(A=\left(2\sqrt{12}-\sqrt{75}+\dfrac{1}{2}\sqrt{48}\right):\sqrt{3}\)
\(A=\left(4\sqrt{3}-5\sqrt{3}+2\sqrt{3}\right):\sqrt{3}\)
\(A=\sqrt{3}:\sqrt{3}\)
\(A=1\)
b) \(B=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(B=\left|2-\sqrt{5}\right|-\left|\sqrt{5}+1\right|\)
\(B=-2+\sqrt{5}-\sqrt{5}-1\)
\(B=-3\)
c) \(C=\dfrac{3}{\sqrt{7}-2}-\dfrac{4}{3+\sqrt{7}}\)
\(C=\dfrac{3\left(\sqrt{7}+2\right)}{\left(\sqrt{7}-2\right)\left(\sqrt{7}+2\right)}-\dfrac{4\left(3-\sqrt{7}\right)}{\left(3+\sqrt{7}\right)\left(3-\sqrt{7}\right)}\)
\(C=\dfrac{3\left(\sqrt{7}+2\right)}{3}-\dfrac{4\left(3-\sqrt{7}\right)}{2}\)
\(C=\sqrt{7}+2-2\left(3-\sqrt{7}\right)\)
\(C=\sqrt{7}+2-6+2\sqrt{7}\)
\(C=3\sqrt{7}-4\)
d) \(D=3\sqrt{2a}-\sqrt{18a^3}+4\sqrt{\dfrac{a}{2}}-\dfrac{1}{4}\sqrt{128a}\)
\(D=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)
\(D=5\sqrt{2a}-3a\sqrt{2a}-2\sqrt{2a}\)
\(D=3\sqrt{2a}-3a\sqrt{2a}\)
e) \(E=\dfrac{3+\sqrt{3}}{\sqrt{3}}-\dfrac{2}{\sqrt{3}-1}\)
\(E=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(E=\left(\sqrt{3}+1\right)-\dfrac{2\left(\sqrt{3}+1\right)}{2}\)
\(E=\left(\sqrt{3}+1\right)-\left(\sqrt{3}+1\right)\)
\(E=0\)
Đúng 3
Bình luận (0)
Lời giải:
a.
\(A=2\sqrt{\frac{12}{3}}-\sqrt{\frac{75}{3}}+\frac{1}{2}\sqrt{\frac{48}{3}}=2\sqrt{4}-\sqrt{25}+\frac{1}{2}\sqrt{16}\)
\(2.2-5+\frac{1}{2}.4=1\)
b.
\(B=|2-\sqrt{5}|-|\sqrt{5}+1|=\sqrt{5}-2-(\sqrt{5}+1)=-3\)
c.
\(C=\frac{3(\sqrt{7}+2)}{(\sqrt{7}-2)(\sqrt{7}+2)}-\frac{4(3-\sqrt{7})}{(3+\sqrt{7})(3-\sqrt{7})}\)
\(=\frac{3(\sqrt{7}+2)}{7-2^2}-\frac{4(3-\sqrt{7})}{3^2-7}\)
\(=\frac{3(\sqrt{7}+2)}{3}-\frac{4(3-\sqrt{7})}{2}=\sqrt{7}+2-2(3-\sqrt{7})=-4+3\sqrt{7}\)
e.
\(E=\frac{\sqrt{3}(\sqrt{3}+1)}{\sqrt{3}}-\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\sqrt{3}+1-\frac{2(\sqrt{3}+1)}{3-1^2}=(\sqrt{3}+1)-(\sqrt{3}+1)=0\)
Đúng 1
Bình luận (0)
giúp e câu a vs câu c ạ
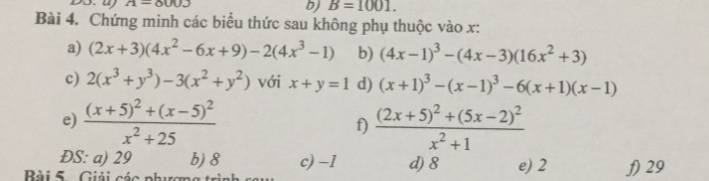
a) \(\left(2x+3\right)\left(4x^2-6x+9\right)-2\left(4x^3-1\right)\)
\(=\left(2x+3\right)\left[\left(2x\right)^2-2x\cdot3+3^2\right]-2\left(4x^3-1\right)\)
\(=\left[\left(2x\right)^3+3^3\right]-2\left(4x^3-1\right)\)
\(=\left(8x^3+27\right)-8x^3+2\)
\(=8x^3+27-8x^3+2\)
\(=29\)
Vậy: ....
c) \(2\left(x^3+y^3\right)-3\left(x^3+y^3\right)\)
\(=2\left(x+y\right)\left(x^2-xy+y^2\right)-3x^2-3y^2\)
\(=2\left(x^2-xy+y^2\right)\cdot1-3x^2-3y^2\)
\(=2x^2-2xy+2y^2-3x^2-3y^2\)
\(=-x^2-2xy-y^2\)
\(=-\left(x^2+2xy+y^2\right)\)
\(=-\left(x+y\right)^2\)
\(=-\left(1\right)^2=-1\)
Vậy: ...
Đúng 1
Bình luận (0)
Giúp e câu a vs câu c với ạ
a, Ta có : \(\sin^2x+\cos^2x=1\)
\(\Rightarrow\sin x=\sqrt{1-\cos^2x}=\left|\dfrac{\sqrt{15}}{4}\right|\)
Mà \(0< x< \dfrac{\pi}{2}\)
\(\Rightarrow\sin x=\dfrac{\sqrt{15}}{4}\)
Ta lại có : \(\left\{{}\begin{matrix}\sin2x=2\sin x\cos x=\dfrac{\sqrt{15}}{8}\\\cos2x=2\cos^2x-1=-\dfrac{7}{8}\end{matrix}\right.\)
Vậy ...
c, Ta có : \(\tan2x=\dfrac{2\tan x}{1-\tan^2x}=\dfrac{4}{3}=\dfrac{\sin2x}{\cos2x}\)
- Ta có HPT : \(\left\{{}\begin{matrix}\sin^22x+\cos^22x=1\\3\sin2x-4\cos2x=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sin2x=\left|\dfrac{4}{5}\right|\\\cos2x=\left|\dfrac{3}{5}\right|\end{matrix}\right.\)
Lại có : \(\pi< x< \dfrac{3}{2}\pi\)
\(\Rightarrow\left\{{}\begin{matrix}\sin2x=\dfrac{4}{5}\\\cos2x=\dfrac{3}{5}\end{matrix}\right.\)
Vậy ...
Đúng 2
Bình luận (0)
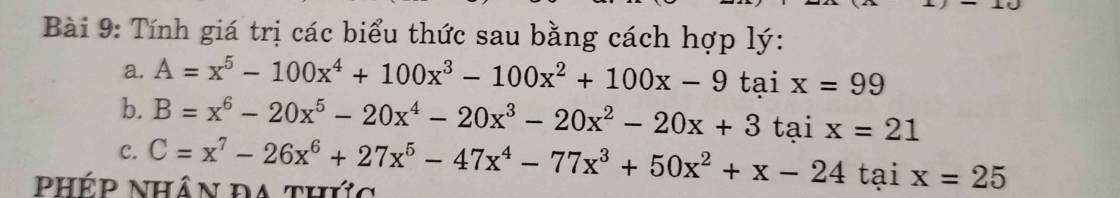 giúp e câu b,c vs ạ
giúp e câu b,c vs ạ
`@` `\text {Ans}`
`\downarrow`
`b,`
\(B=x^6 - 20x^5 - 20x^4 - 20x^3 - 20x^2 - 20x + 3\) tại `x=21`
Ta có: `20 = 21 - 1 => 20 = x-1`
Thay `20 = x-1` vào, ta có:
\(x^6-\left(x-1\right)x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x+3\)
`=`\(x^6-x^6+x^5-x^5+x^4-x^4+...+x+3\)
`=`\(x+3\)
`=`\(21+3=24\)
Vậy, `B=24`
Đúng 2
Bình luận (0)
`c,`
`C=`\(x^7-26x^6+27x^5-47x^4-77x^3+50x^2+x-24\) tại `x=25`
`=`\(x^7-25x^6-x^6+25x^5+2x^5-50x^4+3x^4-75x^3-2x^3+50x^2+x-24\)
`=`\(x^6\left(x-25\right)-x^5\left(x-25\right)+2x^4\left(x-25\right)+3x^3\left(x-25\right)-2x^2\left(x-25\right)+x-24\)
`=`\(\left(x^6-x^5+2x^4+3x^3-2x^2\right)\left(x-25\right)+x-24\)
Thay `x=25` vào bt C, ta được:
\(\left(25^6-25^5+2\cdot25^4+3\cdot25^3-2\cdot25^2\right)\left(25-25\right)+25-24\)
`=`\(\left(25^6-25^5+2\cdot25^4+3\cdot25^3-2\cdot25^2\right)\cdot0+1\)
`= 0+1=1`
Vậy, `C=1.`
Đúng 2
Bình luận (0)
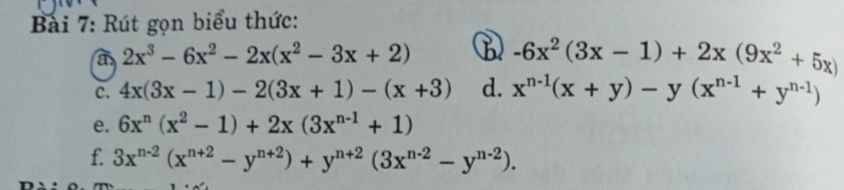 giúp e câu a,b vs ạ
giúp e câu a,b vs ạ
\(a,2x^3-6x^2-2x\left(x^2-3x+2\right)\)
\(=2x^3-6x^2-2x^3+6x^2-4x\)
\(=\left(2x^3-2x^3\right)+\left(-6x^2+6x^2\right)-4x\)
\(=0+0-4x\)
\(=-4x\)
\(b,-6x^2\left(3x-1\right)+2x\left(9x^2+5x\right)\)
\(=-18x^3+6x^2+18x^3+10x^2\)
\(=\left(-18x^3+18x^3\right)+\left(6x^2+10x^2\right)\)
\(=0+16x^2\)
\(=16x^2\)
Đúng 4
Bình luận (1)
a. \(2x^3-6x^2-2x\left(x^2-3x+2\right)\\ =2x^3-6x^2-2x^3+6x^2-4x\\ =-4x\)
b. \(-6x^2\left(3x-1\right)+2x\left(9x^2+5x\right)\\ =-18x^3+6x^2+18x^3+10x^2\\ =6x^2+10x^2\\ =16x^2\)
Đúng 2
Bình luận (1)
Giải giúp e câu a, b vs ạ
Giúp e câu a,b,d vs ạ! E xin cảm ơn
\(b,\left(1\right)4Al+3O_2\underrightarrow{^{to}}2Al_2O_3\\ \left(2\right)Al_2O_3+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2O\\ \left(3\right)Al_2\left(SO_4\right)_3+3BaCl_2\rightarrow3BaSO_4\downarrow+2AlCl_3\\ \left(4\right)AlCl_3+3AgNO_3\rightarrow Al\left(NO_3\right)_3+3AgCl\downarrow\\ \left(5\right)Al\left(NO_3\right)_3+3KOH\rightarrow Al\left(OH\right)_3\downarrow+3KNO_3\\ \left(6\right)2Al\left(OH\right)_3\underrightarrow{^{to}}Al_2O_3+3H_2O\)
Đúng 0
Bình luận (0)
\(d,\left(1\right)3Fe+2O_2\underrightarrow{^{to}}Fe_3O_4\\ \left(2\right)Fe_3O_4+4CO\underrightarrow{^{to}}3Fe+4CO_2\\ \left(3\right)FeO+H_2\underrightarrow{^{to}}Fe+H_2O\\ \left(4\right)Fe+4HNO_3\rightarrow Fe\left(NO_3\right)_3+NO+2H_2O\\ \left(5\right)2Fe\left(NO_3\right)_3+Fe\rightarrow3Fe\left(NO_3\right)_2\\ \left(6\right)Fe\left(NO_3\right)_2+2KOH\rightarrow Fe\left(OH\right)_2\downarrow+2KNO_3\\ \left(7\right)4Fe\left(OH\right)_2+O_2+2H_2O\rightarrow4Fe\left(OH\right)_3\)
Đúng 0
Bình luận (0)
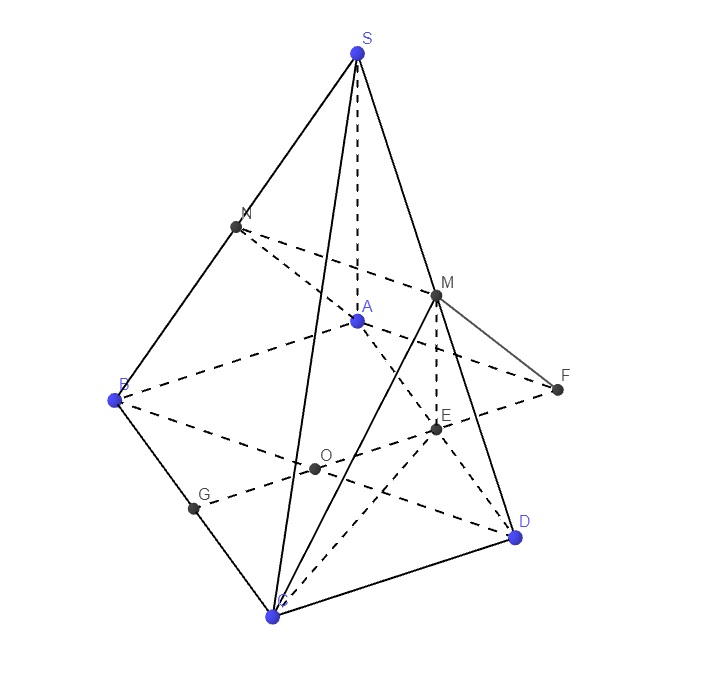
giúp e câu c, e vs ạ
c.
Gọi E là trung điểm AD \(\Rightarrow EM\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}EM=\dfrac{1}{2}SA=a\\EM||SA\Rightarrow EM\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow EC\) là hình chiếu vuông góc của CM lên (ABCD)
\(\Rightarrow\widehat{MCE}\) là góc giữa SM và (ABCD)
\(ED=\dfrac{1}{2}AD=a\Rightarrow EC=\sqrt{CD^2+ED^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{MCE}=\dfrac{EM}{EC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{MCE}=...\)
e.
Gọi O là trung điểm BD, qua A kẻ đường thẳng song song BD cắt OE kéo dài tại F
\(\Rightarrow ABOF\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\left\{{}\begin{matrix}AF=OB=\dfrac{1}{2}BD\\AF||BD\end{matrix}\right.\)
Lại có MN là đường trung bình tam giác SBD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}MN=AF\\MN||AF\end{matrix}\right.\) \(\Rightarrow ANMF\) là hình bình hành
\(\Rightarrow AN||MF\Rightarrow\left(AN;CM\right)=\left(AN;MF\right)=\widehat{CMF}\) nếu nó ko tù hoặc bằng góc bù của nó nếu \(\widehat{CMF}\) là góc tù
Ta có: \(MF=AN=\dfrac{a\sqrt{5}}{2}\) ; \(CM=\sqrt{CE^2+EM^2}=a\sqrt{3}\)
ABOF là hình bình hành nên AODF cũng là hình bình hành \(\Rightarrow E\) là tâm hình bình hành
\(\Rightarrow EF=OF=\dfrac{AB}{2}=\dfrac{a}{2}\)
Gọi G là giao điểm OE và BC \(\Rightarrow FG=EG+EF=a+\dfrac{a}{2}=\dfrac{3a}{2}\)
\(\Rightarrow CF=\sqrt{FG^2+CG^2}=\dfrac{a\sqrt{13}}{2}\)
ĐỊnh lý hàm cos:
\(cos\widehat{CMF}=\dfrac{CM^2+MF^2-CF^2}{2CM.MF}=\dfrac{\sqrt{15}}{15}\Rightarrow\widehat{CMF}\)
Đúng 1
Bình luận (2)