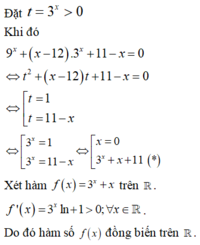3(x²+x²)+x1²x2²=11
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
cho phương trình x^2-2x+m-2. Tìm giá trị m để pt có 2 nghiệm x1,x2 thoả mãn 3(x1²+x2²)+x1²x2²=11
Câu 1 : Giả sử x và y là 2 đại lượng tỉ lệ thuận , x1 , x2 là 2 giá trị khác nhau của x ; y1 , y2 là 2 giá trị khác nhau của y
a) Tính x1 biết x2=2 , y1= -3/4 , y2 = 1/7
b) Tính x2 biết x1=11/7 . y1 = 11/2 , y2 = -9/3
\(a,y_2=kx_2\Rightarrow k=\dfrac{1}{7}:2=\dfrac{1}{14}\\ \Rightarrow y_1=\dfrac{1}{14}x_1\\ \Rightarrow x_1=-\dfrac{3}{4}:\dfrac{1}{14}=-\dfrac{21}{2}\\ b,y_1=kx_1\Rightarrow k=\dfrac{11}{2}:\dfrac{11}{7}=\dfrac{7}{2}\\ \Rightarrow y_2=\dfrac{7}{2}x_2\Rightarrow x_2=-\dfrac{9}{3}:\dfrac{7}{2}=-\dfrac{6}{7}\)
Đúng 1
Bình luận (0)
Cho phương trình: \(x^2\)- 3x + m - 3 = 0. Tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn: \(x1^2\) + 3x2 = \(x1^2\)\(x2^2\) - 11
Gọi x1 x2 x3 là 3 nghiệm của pt x3-x+1=0 ..Tính x111+x211+x311
(Đề kh sai đâu nha các bạn)
Mong nhận được phản hồi của các bạn sớm nhất có thể
sai rồi pt chỉ có 1 nghiệm thực thôi 2 nghiệm phức mà bộ giáo dục đâu cho học số phức nữa
Đúng 0
Bình luận (0)
Giả sử x,y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x, y1;y2 là hai giá trị tương ứng của y
1. Tính x2 biết x1=11/7, y1=11/2,y2=-7/3
2. Tính x1,y1 biết 2y1 + 3x1 = 20, x2=-6, y2=3
1: Vì x và y tỉ lệ thuận nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
hay \(x_2=\dfrac{x_1\cdot y_2}{y_1}=\left(\dfrac{11}{7}\cdot\dfrac{-7}{3}\right):\dfrac{11}{2}=\dfrac{-11}{3}\cdot\dfrac{2}{11}=\dfrac{-2}{3}\)
2: Ta có: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
nên \(\dfrac{x_1}{-6}=\dfrac{y_1}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{-6}=\dfrac{y_1}{3}=\dfrac{3x_1+2y_1}{3\cdot\left(-6\right)+2\cdot3}=\dfrac{20}{-12}=\dfrac{-5}{3}\)
Do đó: \(x_1=10;y_2=-5\)
Đúng 0
Bình luận (0)
Cho phương trình
9
x
+
x
-
12
.
3
x
+
11
-
x
0
. Phương trình trên có hai nghiệm
x
1
,
x
2
. Giá trị...
Đọc tiếp
Cho phương trình 9 x + x - 12 . 3 x + 11 - x = 0 . Phương trình trên có hai nghiệm x 1 , x 2 . Giá trị S = x 1 + x 2 bằng bao nhiêu?
A. S = 0
B. S = 2
C. S = 4
D. S = 6
8.1. Tìm m để pt: x2 - (m+9)x - 7 = 0 có 2 nghiệm phân biệt x1, x2 thỏa mãn x1<x2 và |x1| - |x2| =16.
8.2. Tìm m để pt: x2 + (m+12)x - 11 =0 có 2 nghiệm phân biệt x1, x2 thỏa mãn x1>x2 và |x1| - |x2| =15.
8.1/ Để phương trình có 2 nghiệm phân biệt thì \(\Delta=\left(m-9\right)^2-4.\left(-7\right)=m^2-18m+109>0\Leftrightarrow m\in R\)
Theo định lý viete, ta có: \(\left\{{}\begin{matrix}x_1+x_2=m+9\\x_1x_2=-7< 0\end{matrix}\right.\)
\(\left|x_1\right|-\left|x_2\right|=16\Leftrightarrow x_1^2+x_2^2-2\left|x_1x_2\right|=256\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|=256\Leftrightarrow\left(m+9\right)^2=256-2\left(-7\right)-2\left|-7\right|=256\)
\(\Leftrightarrow\left(m+9\right)^2=256\Leftrightarrow\left[{}\begin{matrix}m=7\\m=-25\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=7\\m=-25\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình
9
x
+
(
x
-
12
)
.
3
x
+
11
-
x
0
. Phương trình trên có hai nghiệm x1,x2. Giá trị Sx1+x2 bằng bao nhiêu? A. S0 B. S2 C. S4 D. S6
Đọc tiếp
Cho phương trình 9 x + ( x - 12 ) . 3 x + 11 - x = 0 . Phương trình trên có hai nghiệm x1,x2. Giá trị S=x1+x2 bằng bao nhiêu?
A. S=0
B. S=2
C. S=4
D. S=6
Cho pt : x² - 2(m + 2)x + 6m +1 = 0 ( * )
1) Cm : (*) luôn có 2 nghiệm pb x1,x2
2) Tìm m để (*) có 2 nghiệm thoả :
a) x1 < 2 < x2
b) 1 < x1 < x2
c) x1 < x2 < 3
3) Tìm m để 2x1 = x2 - 1
4) Tìm m để : x1(x1⁴ + 1) + x2( 32x2⁴ +1 ) = x1x2+11/3
5) Tìm m để x1,x2 thuộc Z