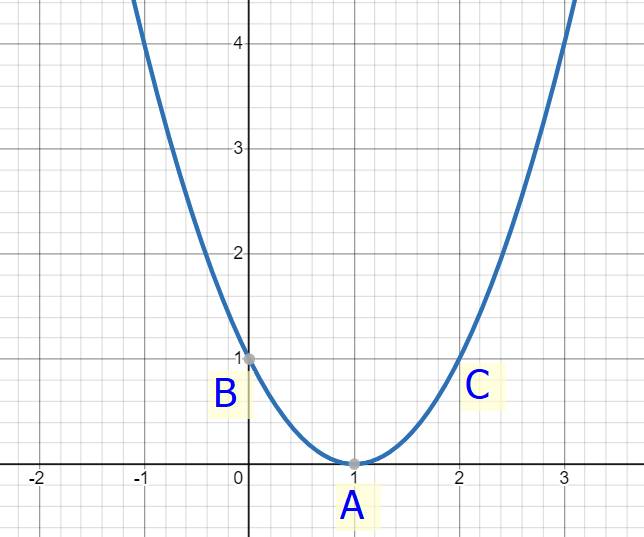
Xác định giao điểm của đồ thị hàm số y=x−1 với trục tung trục hoành

Những câu hỏi liên quan
Cho hàm số y=(m-1)x+m
a) Xác định m để đồ thị hàm số cắt trục tung điểm có tung độ bằng 3, cắt trục hoành tại điểm có hoành độ bằng 3
b) Vẽ đồ thị hàm số của hai hàm số ứng với m tìm được câu a
c) Gọi giao điểm của 2 đồ thị với trục hoành lần lượt là A;B giao điểm của 2 đồi thị là C. Tính chu vi và diện tích của tam giác ABC
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
Đúng 0
Bình luận (0)
Cho hàm số y=(m-1)x+m
a) Xác định m để đồ thij hàm số cắt trục tung điểm có tung độ bằng 3, cắt trục hoành tại điểm có tung độ bằng 3
b) Vẽ đồ thị hàm số của hai hàm số ứng với m tìm được câu a
c) Gọi giao điểm của 2 đồ thị với trục hoành lần lượt là A; B giao điiểm của hai đồ thị là C. Tính chu vi và diện tích của tam giác ABC
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
Đúng 0
Bình luận (0)
2, Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
cho hàm số y (m-1)x + m - 5a) xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3b) xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -1c) xác định m để đồ thị hàm số đi qua gốc tọa độ
Đọc tiếp
cho hàm số y = (m-1)x + m - 5
a) xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3
b) xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -1
c) xác định m để đồ thị hàm số đi qua gốc tọa độ
a: Thay x=0 và y=3 vào y=(m-1)x+m-5, ta được:
\(0\cdot\left(m-1\right)+m-5=3\)
=>m-5=3
=>m=8
b: Thay x=-1 và y=0 vào y=(m-1)x+m-5, ta được:
\(-\left(m-1\right)+m-5=0\)
=>-m+1+m-5=0
=>-4=0(vô lý)
c: Thay x=0 và y=0 vào y=(m-1)x+m-5, ta được:
\(0\left(m-1\right)+m-5=0\)
=>m-5=0
=>m=5
Đúng 1
Bình luận (0)
cho hàm số y(2m+1)x-m+3 (1) a,xác định giá trị của m để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng. b,xác định giá trị của m để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3. c,vẽ đồ thị của hàm số ứng với giá trị của m vừa tìm được ở các câu a và b trên cùng hệ trục toạ độ oxy.tìm giao điểm của hai đường thẳng vừa vẽ được. d,tìm điểm cố định mà đồ thị hàm số (1) luôn đi qua vớ...
Đọc tiếp
cho hàm số y=(2m+1)x-m+3 (1) a,xác định giá trị của m để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng. b,xác định giá trị của m để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3. c,vẽ đồ thị của hàm số ứng với giá trị của m vừa tìm được ở các câu a và b trên cùng hệ trục toạ độ oxy.tìm giao điểm của hai đường thẳng vừa vẽ được. d,tìm điểm cố định mà đồ thị hàm số (1) luôn đi qua với mọi m
a: Bạn bổ sung đề đi bạn
b: thay x=-3 và y=0 vào (d), ta được:
\(-3\left(2m+1\right)-m+3=0\)
=>-6m-3-m+3=0
=>-7m=0
=>m=0
d: y=(2m+1)x-m+3
=2mx+x-m+3
=m(2x-1)+x+3
Tọa độ điểm cố định mà (1) luôn đi qua là:
\(\left\{{}\begin{matrix}2x-1=0\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=3+\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số y = (a - 2)x + a
a) Xác định a để đồ thị hàm số cắt trục tung tại điểm có tung độ = 2.
b) Xác định giá trị của a để đồ thị hàm số cắt trục hoành tại điểm có hoành độ = -1.
c) Vẽ đồ thi của 2 hàm số ứng với giá trị của a tìm được ở câu a, b trên cùng hệ trực tọa độ Oxy. Và tìm tọa độ giao điểm của 2 đường thẳng vừa vẽ được.
a: Thay x=0 và y=2 vào (d), ta được:
a=2
b: Thay x=-1 và y=0 vào (d), ta được:
\(-\left(a-2\right)+a=0\)
\(\Leftrightarrow2=0\)(vô lý)
Đúng 0
Bình luận (0)
vẽ đồ thị hàm số y=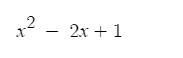 , xác định tọa độ đỉnh, vẽ trục đối cứng , xác định điểm đặc biệt, chẳng hạn: giao điểm với trục tung và trục hoành nếu có.
, xác định tọa độ đỉnh, vẽ trục đối cứng , xác định điểm đặc biệt, chẳng hạn: giao điểm với trục tung và trục hoành nếu có.
Ta có: \(y=x^2-2x+1\), có: \(a=1>0;b=-2;c=1\)
+ Tập xác định: \(D=R\)
+ Nghịch biến trên: \(\left(-\infty;1\right)\); đồng biến trên \(\left(1;+\infty\right)\)
Bảng biến nhiên:
| x | \(-\infty\) 1 \(+\infty\) |
| y | \(+\infty\) → 0 → \(-\infty\) |
+ Đồ thị hàm số parabol có:
Đỉnh: \(A\left(1;0\right)\)
Trục đối xứng là đường thẳng x = 1
Giao điểm với Oy tại \(B\left(0;1\right)\), điểm đối xứng với B qua đường thẳng x = 1 là \(C\left(2;1\right)\)
Đi qua các điểm \(\left(-1;4\right);\left(3;4\right)\)
Đúng 2
Bình luận (1)
3) cho hàm số yleft(a-1right)x+a ane1 (1)a) chứng tỏ: đồ thị hàm số (1) luôn đi qua (-1; 1)b) xác định a để đồ thị 91) cắt trục tung tại điểm có tung độ 3. Vẽ đồ thị hàm số c) xác định a để đồ thị (1) cắt trục hoành tại điểm có hoành độ là -2. Tính khỏng cách từ gốc tọa độ O đến đường thẳnglm nhanh giúp mk nhé mk đang cần gấp
Đọc tiếp
3) cho hàm số \(y=\left(a-1\right)x+a\) \(a\ne1\) (1)
a) chứng tỏ: đồ thị hàm số (1) luôn đi qua (-1; 1)
b) xác định a để đồ thị 91) cắt trục tung tại điểm có tung độ 3. Vẽ đồ thị hàm số
c) xác định a để đồ thị (1) cắt trục hoành tại điểm có hoành độ là -2. Tính khỏng cách từ gốc tọa độ O đến đường thẳng
lm nhanh giúp mk nhé mk đang cần gấp
Cho hàm số yleft(a-1right)x+a
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a), b) trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được
Đọc tiếp
Cho hàm số \(y=\left(a-1\right)x+a\)
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a), b) trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được
cho hàm số y = ( a - 1)x + a
a, Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có hoành độ bằng 2.
b, Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có hoành độ bằng -3
Đặt (d) : y = (a-1)x + a
a/ Bạn chú ý : (d) cắt trục tung do vậy (d) sẽ đi qua điểm có TUNG ĐỘ bằng 2 nhé (chứ không phải hoành độ)
Đồ thị hàm số (d) đi qua điểm \(\left(0;2\right)\)do vậy : \(2=\left(a-1\right).0+a\Rightarrow a=2\)
b/ Tương tự
Đúng 0
Bình luận (0)