nhờ thầy cô giúp em phần môn toán với ạ


Nhờ thầy cô giáo và các bạn giúp đỡ theo kiến thức học kì 1 -- Toán Lớp 8 với ạ.
Cám ơn thầy cô nhiều ạ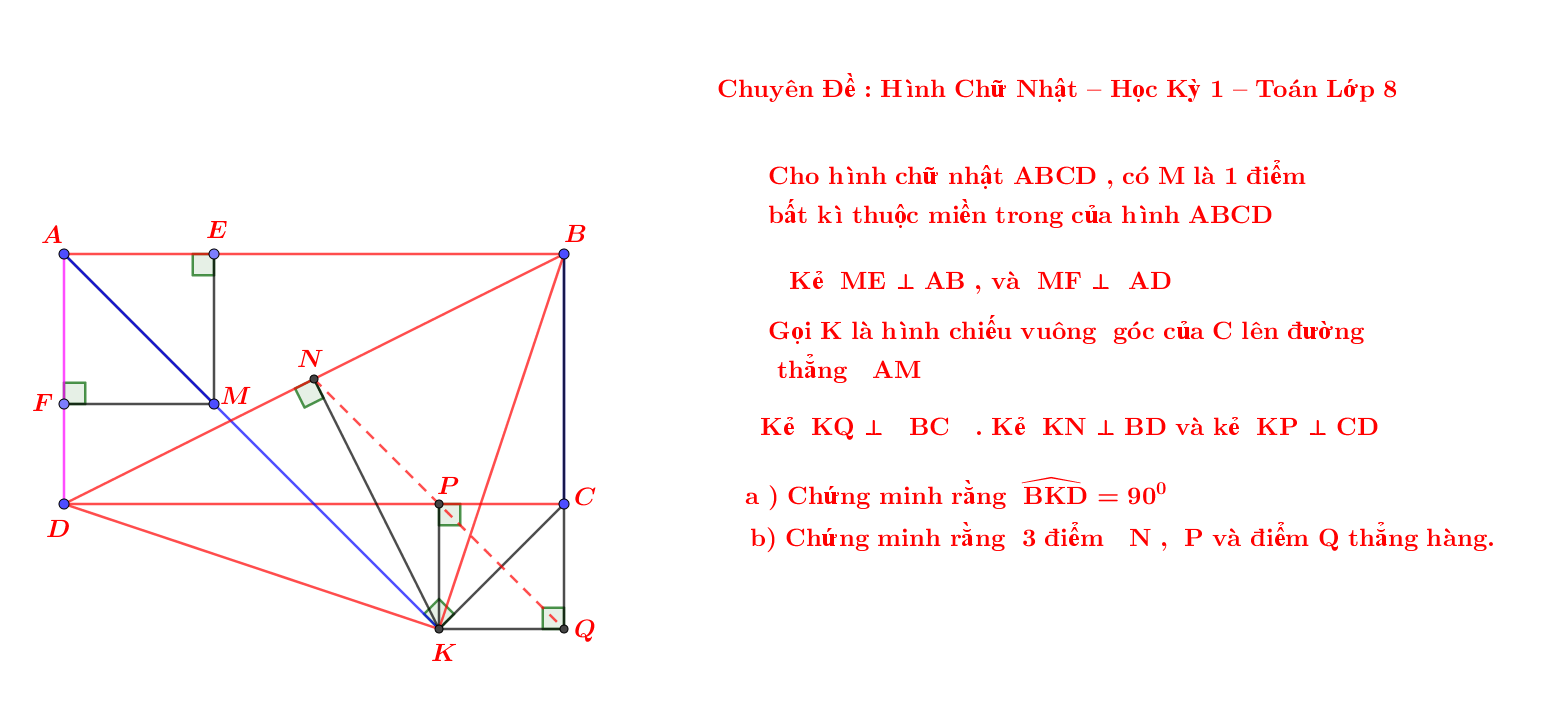
Xin nhờ quý thầy cô và các bạn yêu toán gần xa giúp đỡ với ạ!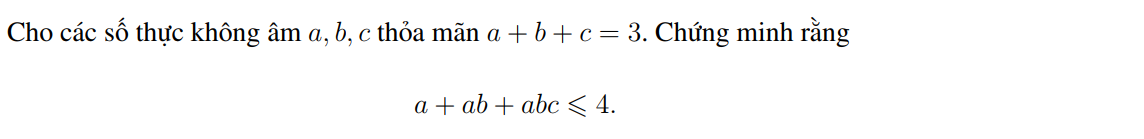
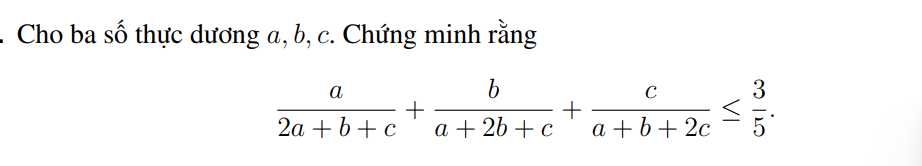
Áp dụng BĐT cosi dạng \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\cdot\dfrac{1}{4}\ge\dfrac{4}{a+b}\cdot\dfrac{1}{4}\\ \Leftrightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\Leftrightarrow\dfrac{a}{2a+b+c}=\dfrac{a}{a+b+a+c}\le\dfrac{a}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b}{a+2b+c}\le\dfrac{b}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)\\\dfrac{c}{a+b+2c}\le\dfrac{c}{4}\left(\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)\end{matrix}\right.\)
Cộng VTV 3 BĐT trên:
\(\Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\\ \Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{1}{4}\cdot3=\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow a=b=c\)
trong dạng bài tính toán với số thập phân
trong phần hướng dẫn giải và phần kiểm tra đáp án thì 2 đáp số khác nhau em muốn nhờ thầy cô giải thích giúp em
Tìm ba số nguyên tố \(p;q;r\) thỏa mãn : \(p^2+q^2+r^2=5054\)
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Nếu p;q;r đều lẻ hoặc có đúng 1 số trong 3 số là lẻ \(\Rightarrow p^2+q^2+r^2\) lẻ, trong khi 5054 chẵn (ktm)
\(\Rightarrow\) Cả p;q;r đều chẵn (loại do \(2^2+2^2+2^2< 5054\)) hoặc có đúng 1 số trong 3 số là chẵn
Do vai trò 3 số như nhau, ko mất tính tổng quát, giả sử r chẵn \(\Rightarrow r=2\)
\(\Rightarrow p^2+q^2=5050\)
Nếu p; q đều chia hết cho 3 \(\Rightarrow p=q=3\Rightarrow ktm\)
Nếu p;q đều ko chia hết cho 3 \(\Rightarrow p^2\) và \(q^2\) đều chia 3 dư 1
\(\Rightarrow p^2+q^2\) chia 3 dư 2 trong khi \(5050\) chia 3 dư 1 (ktm)
\(\Rightarrow\) Có đúng 1 số trong p; q chia hết cho 3, ko mất tính tổng quát, giả sử là p \(\Rightarrow p=3\)
\(\Rightarrow q^2=5050-9=5041\Rightarrow q=71\) là SNT (thỏa mãn)
Vậy bộ 3 số nguyên tố thỏa mãn là \(\left(2;3;71\right)\) và các hoán vị
Vì tổng của p2 + q2 + r2 \(⋮2\)
=> \(\left[{}\begin{matrix}p⋮2\\q⋮2\\r⋮2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}p=2\\q=2\\r=2\end{matrix}\right.\);
Giả sử r = 2 => p2 + q2 = 5050 ; p;q lẻ
=> Chữ số tận cùng p2 chỉ có thể là 9;1
=> Chư số tận cùng p là 1;3;7;9
mà p2 + q2 = 5050 => q2 \(< 5050\) ; p2 < 5050
<=> q < 72 (1) ; p < 72 (2)
Lại có p2 + q2 = 5050
<=> 2pq = 5050 - (p - q)2 < 5050
<=> pq \(< 2525\) (3)
Từ (1) ; (3) => p > 35 (4)
Từ (2) ; (4) => 35 < p < 72
<=> p \(\in\left\{37;41;43;47;53;59;61;67;71\right\}\)
Thử từng giá trị p => tìm được p = 71 thỏa mán
thay vào pt gốc được q = 3 (tm)
Vậy các cặp (p;q;r) thỏa là (71;3;2) và các hoán vị
Giả sử p<q<r.
Số 2 là số nguyên tố chẵn duy nhất.
Số lẻ có dạng 2k+1 (k\(\in\)N), bình phương của số lẻ là (2k+1)2=4k2+4k+1 là một số lẻ.
Mà p2+q2+r2 là một số chẵn (=5054), suy ra p=2.
q2+r2=5050 \(\Rightarrow\) q2<2525 \(\Rightarrow\) 3\(\le\)q<50.
Với q=3 \(\Rightarrow\) r=71 (nhận).
Vậy ba số nguyên tố cần tìm là 2, 3 và 71.
Tìm tất cả các số nguyên tố \(p\) sao cho \(8.p^2+1\) là số nguyên tố
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em với ạ!
Em cám ơn nhiều ạ!
Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu
Tìm các số nguyên tố \(p;q;r;s\) phân biệt sao cho \(p^3+q^3+r^3+s^3=1709\)
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán , gợi ý giúp đỡ em bài toán với ạ!
Em cám ơn nhiều lắm ạ!
Tìm tất cả các số nguyên tố \(p\) sao cho \(2^p+p^2\) cũng là số nguyên tố ?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em bài toán về chủ đề : Đồng Dư Thức với ạ!
Em cám ơn nhiều ạ!
Với p = 2 => 2p + p2 = 8 (loại)
Với p = 3 => 23 + 32 = 17 (loại)
Nhận thấy với p > 3 => p lẻ
Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Khi đó P = 2p + p2
= (2p + 1) + (p2 - 1)
Vì p lẻ => 2p + 1 = (2 + 1).(2p - 1 - 2p - 2 + ... + 1) \(⋮3\)(1)
Với p = 3k + 1 => p2 - 1 = (p - 1)(p + 1) = (3k + 1 - 1)(3k + 1 + 1)
= 3k(3k + 2) \(⋮3\) (2)
Từ (1) ; (2) => P \(⋮3\)(loại)
Với p = 3k + 2 => p2 - 1 = (p - 1)(p + 1) = (3k + 2 - 1)(3k + 2 + 1)
= 3(k + 1)(3k + 1) \(⋮\)3 (3)
Từ (1) ; (3) => P \(⋮3\)
=> p = 3 là giá trị cần tìm
Xin phép nhờ quý thầy cô giúp đỡ em với ạ!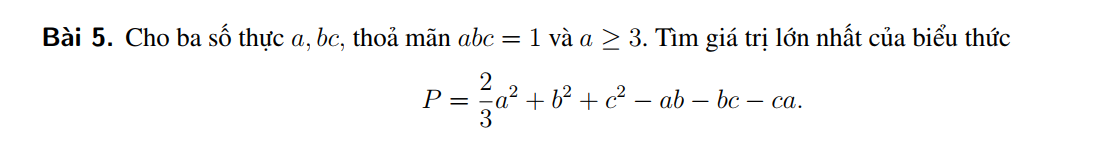
Nhờ thầy cô và các bạn giúp đỡ em với ạ