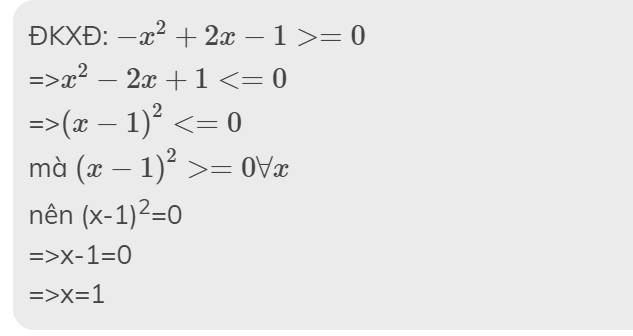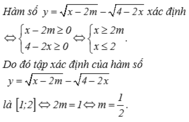xác định khi và chỉ khi xác định khi và chỉ khi Enter
Đọc tiếp
xác định khi và chỉ khi xác định khi và chỉ khi Enter
Những câu hỏi liên quan
Biểu thức log a b xác định khi và chỉ khi
A. a>0, b>0
B. 0<b#1, a>0
C. 0<a#1, b>0
D. a#1, b>0
\(\sqrt{2x+5}\) xác định khi và chỉ khi.
ĐK: \(2x+5\ge0\Leftrightarrow x\ge-\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
\(\sqrt{2x+5}\) xác định chỉ
khi:\(2x+5\ge0\)
\(\Leftrightarrow x\ge-\dfrac{5}{2}\)
Đúng 0
Bình luận (0)
Biểu thức x - 4 xác định khi và chỉ khi
A.x > 4
B.x < 4
C.x ≥ 4
D.x ≤ 4
Đáp án là C
Biểu thức x - 4 xác định khi và chỉ khi
x - 4 ≥ 0 ⇔ x ≥ 4
Đúng 0
Bình luận (0)
Hàm số
y
log
x
−
1
xác định khi và chỉ khi : A.
x
1
x
≠
2
B. x1 C. x0 D.
x
≠
2
Đọc tiếp
Hàm số y = log x − 1 xác định khi và chỉ khi :
A. x > 1 x ≠ 2
B. x>1
C. x>0
D. x ≠ 2
Đáp án A
Hàm số y = log x − 1 x xác định khi x > 0 x − 1 > 0 x − 1 ≠ 1 ⇔ x > 0 x > 1 x ≠ 2 ⇔ x > 1 x ≠ 2
Đúng 0
Bình luận (0)
\(\sqrt{-x^2+2x-1}\) xác định khi và chỉ khi ?
\(\sqrt{-x^2+2x-1}\) xác định khi và chỉ khi ?
ĐKXĐ: \(-x^2+2x-1>=0\)
=>\(x^2-2x+1< =0\)
=>\(\left(x-1\right)^2< =0\)
mà \(\left(x-1\right)^2>=0\forall x\)
nên (x-1)2=0
=>x-1=0
=>x=1
Đúng 0
Bình luận (0)
hàm số y = \(\sqrt{\dfrac{-5}{3-4x}}\) xác định khi và chỉ khi
Điều kiện xác định:
\(\left\{{}\begin{matrix}\dfrac{-5}{3-4x}\ge0\\3-4x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-4x< 0\\3-4x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{3}{4}\\x\ne\dfrac{3}{4}\end{matrix}\right.\)
Vậy để hàm số \(y=\sqrt{\dfrac{-5}{3-4x}}\) xác định thì \(x>\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
Biểu thức \(\sqrt{\dfrac{x^2}{x+1}}\) xác định khi và chỉ khi
ĐKXĐ: \(\dfrac{x^2}{x+1}>=0\)
=>x+1>0
=>x>-1
Đúng 0
Bình luận (0)
Tập xác định của hàm số
y
x
-
2
m
-
4
-
2
x
là [1;2] khi và chỉ khi A.
m
-
1
2
B.
m
1
C.
m
1
2
D.
m
1
3
Đọc tiếp
Tập xác định của hàm số y = x - 2 m - 4 - 2 x là [1;2] khi và chỉ khi
A. m = - 1 2
B. m = 1
C. m = 1 2
D. m > 1 3
