Ba bạn An, Bình, Cường mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1;19].Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng?
A. 2539/6859
B. 2287/6859
C. 109/323
D. 1027/6859
3 bạn A,B,C mỗi bạn viết ngẫu nhiên lên bảng 1 số tự nhiên thuộc đoạn [1;16]. Xác suất để 3 số được viết ra có tổng chia hết cho 3 bằng?
Cho em hỏi cách làm dạng này với ạ :<
Mỗi bạn có 16 cách viết nên số phần tử không gian mẫu là 16^3.
Gọi A là biến cố '3 số được viết ra có tổng chia hết cho 3'
Các số tự nhiên từ 1 đến 16 chia thành 3 nhóm:
Nhóm I gồm các số tự nhiên chia hết cho 3 gồm 5 số.
Nhóm II gồm các số tự nhiên cho 3 dư 1 gồm 6 số.
Nhóm III gồm các số tự nhiên cho 3 dư 2 gồm 5 số.
Để ba số có tổng chia hết cho 3 thì xảy ra các trường hơp sau:
Cả ba bạn viết được số thuộc nhóm I có 5^3 cách.
Cả ba bạn viết được số thuộc nhóm II có 6^3 cách.
Cả ba bạn viết được số thuộc nhóm III có 5^3 cách.
Mỗi bạn viết được một số thuộc một nhóm có 3!×(5×6×5)
=> n(A) = 5^3 + 6^3 + 5^3 + 3!×(5×6×5) = 1366
Vậy P(A) = 1366/16^3
Ba bạn A , B , C mỗi bạn viết ngẫu nhiên một số tự nhiên thuộc đoạn 1;16 được kí hiệu theo thứ tự là a, b, c rồi lập phương trình bậc hai . Xác suất để phương trình lập được có nghiệm kép là
A. 17 2048
B. 5 512
C. 3 512
D. 1 128
Ba bạn A , B , C mỗi bạn viết ngẫu nhiên một số tự nhiên thuộc đoạn 1 ; 16 được kí hiệu theo thứ tự là a, b, c rồi lập phương trình bậc hai a x 2 + 2 b x + c = 0 . Xác suất để phương trình lập được có nghiệm kép là
A. 17 2048
B. 5 512
C. 3 512
D. 1 128
Xếp ngẫu nhiên 5 bạn An, Bình, Cường, Dũng, Đông ngồi vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Xác suất các biến cố ‘hai bạn An và Bình không ngồi cạnh nhau’ là
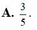
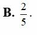
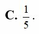
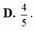
Xếp ngẫu nhiên 5 bạn An, Bình, Cường, Dũng, Đông ngồi vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Xác suất của biến cố “hai bạn An và Bình không ngồi cạnh nhau” là:
A . 3 5
B . 2 5
C . 1 5
D . 4 5
Chọn A
Số phần tử của không gian mẫu: n ( Ω ) = 5!
Gọi A:”Hai bạn An và Bình không ngồi cạnh nhau”
Thì A ¯ :”Hai bạn An và Bình ngồi cạnh nhau”
Xếp An và Bình ngồi cạnh nhau coi như 1 phần tử
- Xếp 1 phần tử (An+Bình) và 3 bạn còn lại theo các thứ tự khác nhau có: 4! Cách
- Xếp 2 học sinh An và Bình ngồi cạnh nhau có 2! cách
Suy ra 
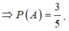
Xếp ngẫu nhiên 5 bạn An, Bình, Cường, Dũng, Đông ngồi vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Xác suất các biến cố ‘hai bạn An và Bình không ngồi cạnh nhau’ là
A. 3 5
B. 2 5
C. 1 5
D. 4 5
Chọn đáp án A
Phương pháp
Sử dụng nguyên lí vách ngăn.
Cách giải
n(Ω)=5!=120
Xếp Cường, Dũng, Đông vào 3 ghế bất kì có 3! cách, khi đó tạo ra 4 khoảng trống. Xếp An và Bình vào hai trong 4 khoảng trống đó có 4.3 = 12 cách.
Gọi A là biến cố: “An và Bình không ngồi cạnh nhau

Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập {0,1,2,3,4,5,6,7,8,9}. Xác suất để trong hai bộ ba số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng
A.-10
B. 203 480
C. 49 60
D. 17 24
Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập {0,1,2,3,4,5,6,7,8,9}. Xác suất để trong hai bộ ba số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng
![]()
![]()
![]()
![]()
Cho tập X = { 1;2;3;4;5 }. Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập X. Tính xác suất để trong hai số đó có đúng một số có chữ số 5
A. 12 25
B. 12 23
C. 21 25
D. 21 23
Số các số tự nhiên có 3 chữ số đôi một khác nhau thuộc tập X là: 5.4.3 = 60.
Trong đó số các số không có mặt chữ số 5 là 4.3.2 = 24 và số các số có mặt chữ số 5 là 60 - 24 = 36.
Gọi A là biến cố hai số được viết lên bảng đều có mặt chữ số 5; B là biến cố hai số được viết lên bảng đều không có mặt chữ số 5.
Rõ ràng A và B xung khắc. Do đó áp dụng quy tắc cộng xác suất ta có:
P A ∪ B = P A + P B = C 36 1 . C 36 1 C 60 1 . C 60 1 + C 24 1 . C 24 1 C 60 1 . C 60 1 = 13 25
Vậy xác suất cần tìm là
P = 1 - P A ∪ B = 1 - 13 25 = 12 25
Đáp án A