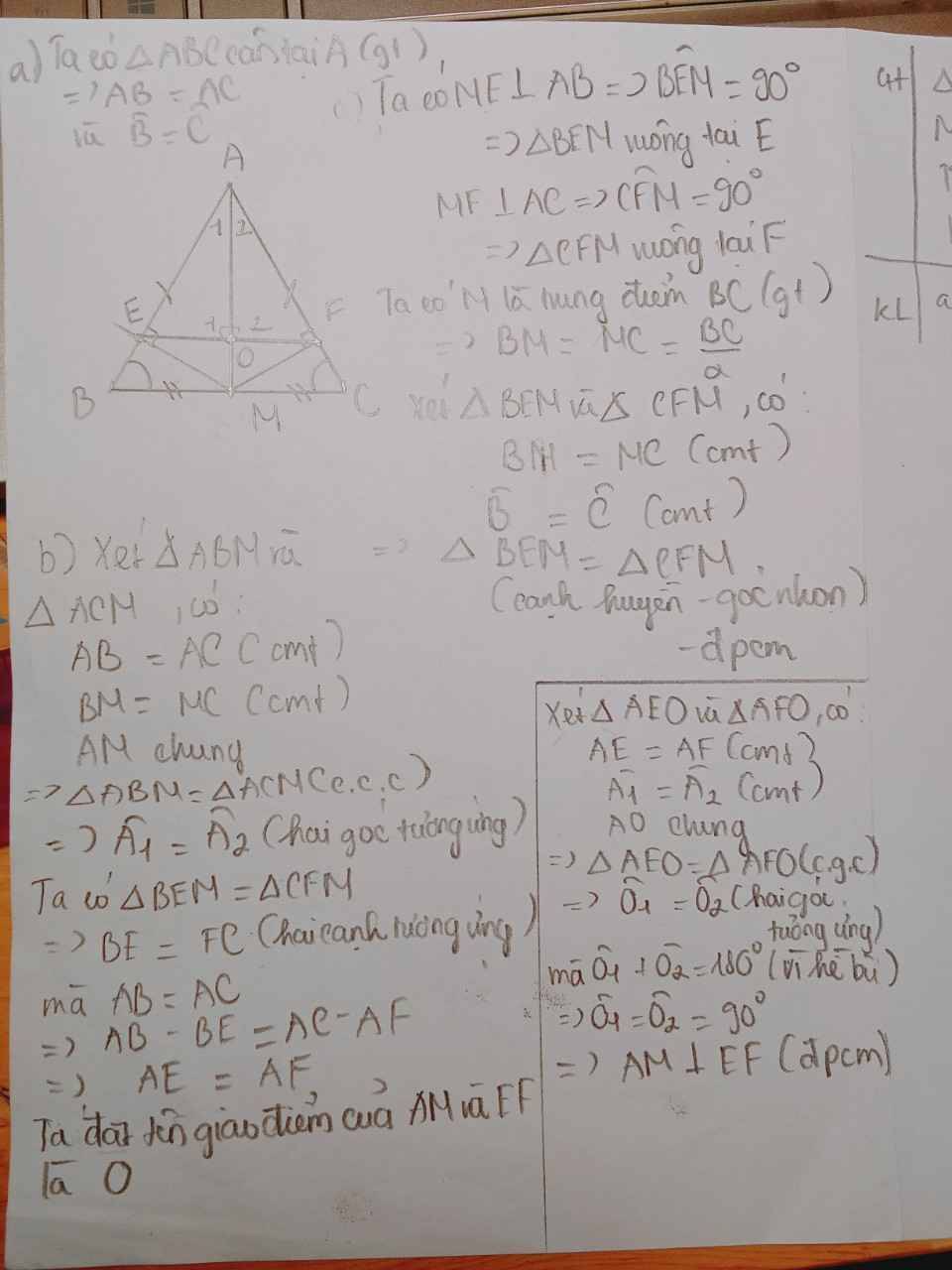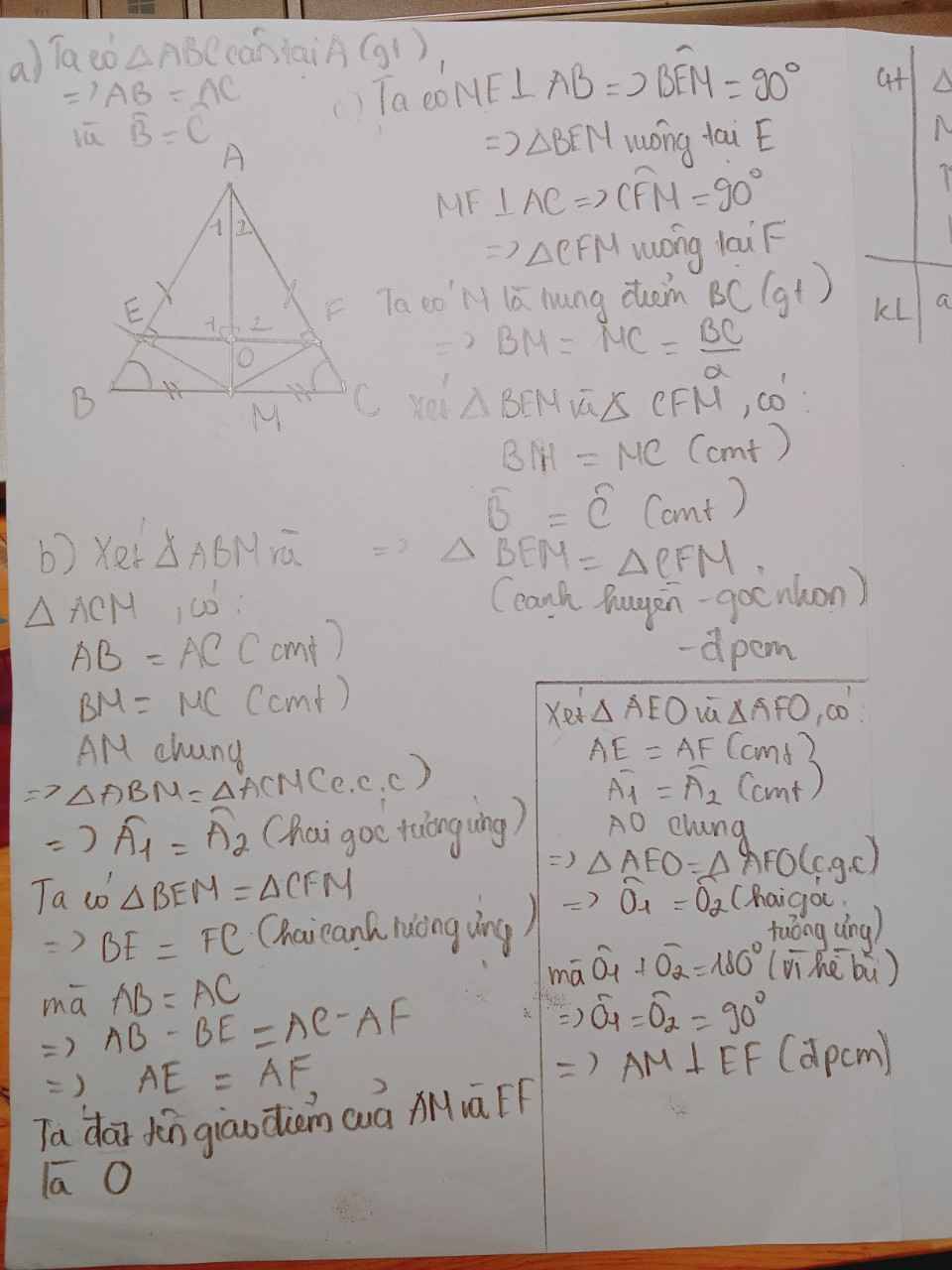Bạn kham khảo link này nhé.

Câu hỏi của Đào Gia Khanh - Toán lớp 7 - Học toán với OnlineMath

đề bài bn cho sai đấy nhé,chỗ "gọi E là giao điểm của ME và AB" ấy, ở đó đáng lẽ pk là F là giao điểm đúng ko? mk đã sửa lại rồi đấy.

a) ta có tam giác ABM=tam giác EBM(CH-GN)

=> AB=EB

gọi H là giao điểm của AE và MB

xét tam giác HBA và tam giác HBE có:

         HB cạnh chung

        \(\widehat{HBA}\)=\(\widehat{HBE}\)(gt)

       AB=EB(cmt)

=> tam giác HBA=tam giác HBE(c.g.c)

=> HA=HE => H là trung điểm của AE(1)

 \(\widehat{AHB}\)=\(\widehat{EHB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AHB}\)=\(\widehat{EHB}\)=90 độ 

=> BH\(\perp\)AE(1)

từ (1) và (2) suy ra BM là trung trực của AE

b) xet 2 tam giác vuông AMF và EMC có:

          AM=ME(vì t.giác ABM=t.giác EBM)

        \(\widehat{AMF}\)=\(\widehat{EMC}\)(vì đối đỉnh)

=> tam giác AMF=tam giác EMC(cạnh góc vuông-góc nhọn kề)

=> MC=MF(2 cạnh tương ứng)

a, Xét tam giác BEM và tam giác CFM có :

Góc BEM = Góc CFM = 90 độ

MB = MC ( gt )

Góc B = Góc C ( gt )

=> Tam giác BEM = Tam giác CFM ( ch-gn )

b, Do tam giác BEM = Tam giác CFM ( câu a, )

=> EB = FC 

E thuộc AB = > AE + EB = AB 

=> AE = AB - EB ( 1 )

F thuộc AC = > AF + FC = AC

=> AF = AC - FC ( 2 )

(1), ( 2 ) => AE = AF 

Gọi I là giao của AM và EF 

AM là đg trung tuyến của tam giác ABC mà tam giác ABC cân 

=> AM là đg phân giác

=> Góc EAI = Góc FAI 

Xét tam giác EAI và tam giác FAI có 

AE = AF ( cmt )

AI chung

Góc EAI = Góc FAI ( cmt )

=> Tam giác EAI = Tam giác FAI ( c-g-c )

=> Góc AME = Góc AMF 

Mà Góc AME + Góc AMF = 180 độ ( 2 góc kề bù ) 

=> Góc AME = Góc AMF = 90 độ

=> AM vuông góc vs EF ( đpcm )

2. Câu hỏi của le thu giang - Toán lớp 7 - Học toán với OnlineMath

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=5^2-3^2=16\)

=>\(AC=\sqrt{16}=4\left(cm\right)\)

b: Sửa đề: ME cắt BA tại K

Xét ΔABM vuông tại A và ΔEBM vuông tại E có

BM chung

\(\widehat{ABM}=\widehat{EBM}\)

Do đó: ΔBAM=ΔBEM

c: Ta có: ΔBAM=ΔBEM

=>BA=BE

Xét ΔBEK vuông tại E và ΔBAC vuông tại A có

BE=BA

\(\widehat{EBK}\) chung

Do đó: ΔBEK=ΔBAC

=>BK=BC

=>ΔBKC cân tại B

d: Ta có: MA+MC=AC

ME+MK=KE

mà AC=KE và MA=ME

nên MK=MC

=>ΔMKC cân tại M

=>\(\widehat{KMC}=180^0-2\cdot\widehat{MKC}\)

mà \(\widehat{KMC}=\widehat{AME}\)(hai góc đối đỉnh)

nên \(\widehat{AME}=180^0-2\cdot\widehat{MKC}\left(1\right)\)

Xét tứ giác BAME có

\(\widehat{BAM}+\widehat{BEM}+\widehat{ABE}+\widehat{AME}=360^0\)

=>\(\widehat{AME}+\widehat{ABC}=180^0\)

=>\(\widehat{AME}=180^0-\widehat{ABC}\left(2\right)\)

Từ (1),(2) suy ra \(\widehat{ABC}=2\cdot\widehat{MKC}\)

a:Xét ΔCAD vuông tại A và ΔCED vuông tại E có

CD chung

góc ACD=góc ECD

=>ΔCAD=ΔCED

=>DA=DE

=>ΔDAE cân tại D

b: CA=CE

DA=DE

=>CD là trung trực của AE

=>MA=ME và CM vuông góc AE tại M

a/  Xét tam giác ABM và tam giác EBM:

+    ^A = ^AEB ( = 90^o)

+    BM chung

+    ^ABM = ^EBM ( do BM là phân giác ^B)

=>  Tam giác ABM = Tam giác EBM (ch - gn)

b/  Ta có: ^A = ^B + ^C = 90^o (do tam giác ABC vuông tại A)

Mà ^C = 30^o (gt)

=> ^B = 60^o

Tam giác ABM = Tam giác EBM (cmt)

=> AB = EB (cặp cạnh tương ứng)

=> Tam giác ABE cân tại B 

Lại có: ^B = 60^o (cmt)

=> Tam giác ABE đều 

a) Xét ΔAMB và ΔEMB có

BA=BE(gt)

\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))

BM chung

Do đó: ΔAMB=ΔEMB(c-g-c)

Suy ra: \(\widehat{MAB}=\widehat{MEB}\)(hai góc tương ứng)

mà \(\widehat{MAB}=90^0\)(ΔABC vuông tại A)

nên \(\widehat{MEB}=90^0\)

hay ME\(\perp\)BC(đpcm)

b) Ta có: ΔABC vuông tại A(gt)

\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)

\(\Leftrightarrow\widehat{ABC}+30^0=90^0\)

\(\Leftrightarrow\widehat{ABC}=60^0\)

hay \(\widehat{ABE}=60^0\)

Xét ΔABE có BA=BE(gt)

nên ΔBAE cân tại B(Định nghĩa tam giác cân)

Xét ΔBAE cân tại B có \(\widehat{ABE}=60^0\)(cmt)

nên ΔBAE đều(Dấu hiệu nhận biết tam giác đều)

a) Xét ΔAMK vuông tại A và ΔCMH vuông tại C có 

MA=MC(M là trung điểm của AC)

\(\widehat{AMK}=\widehat{CMH}\)(hai góc đối đỉnh)

Do đó: ΔAMK=ΔCMH(cạnh góc vuông-góc nhọn kề)

Suy ra: AK=CH(hai cạnh tương ứng)

Xét tứ giác AKCH có 

AK//CH(\(\perp AC\))

AK=CH(cmt)

Do đó: AKCH là hình bình hành(Dấu hiệu nhận biết hình bình hành)