Câu 2. Ta có: a + b = c, gọi c là ______
Một sự khác biệt. B. tổng. C. tổng cộng. D. B & C đều đúng.
( tớ học toán song ngữ nên dịch tiếng việt) hepp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị (C) đường thẳng A, B Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k 1 , k 2 là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k 1 + k 2 lớn nhất
A. -1
B. -2
C. 3
D. -5
Cho a b c d là các số thực dương có tổng bằng một cmr a bình trên a cộng b cộng với b bình trên b cộng c cộng với c bình trên c cộng d cộng với d bình trên d cộng a lớn hơn bằng 1/2
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y=x+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất.
A. m=-1.
B.m=-2 .
C. m=3 .
D. m=-5.
- Phương trình hoành độ giao điểm của d và (C) là
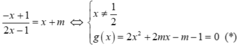
- Theo định lí Viet ta có x1+x2=-m; ![]()
Giả sử A( x1; y1); B( x2; y2).
- Ta có 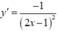 nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là
nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là 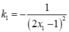 và
và 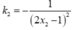 .Vậy
.Vậy
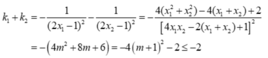
- Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng -2 khi m= -1.
Chọn A.
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
A. -2
B. -1
C. 1
D. 2
+ Phương trình hoành độ giao điểm của d và (C) là
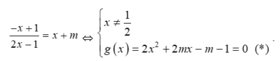
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có y ' = - 1 ( 2 x - 1 ) 2 , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
k 1 = - 1 ( 2 x 1 - 1 ) 2 ; k 2 = - 1 ( 2 x 2 - 1 ) 2

Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.
Cho 6 số nguyên dương phân biệt là a, b, c, d, e, f . Ta tính tổng của mỗi cặp số trong 6
số đó. Hỏi có nhiều nhất bao nhiêu số nguyên tố khác nhau có thể trong các tổng đó?
Cho 69 số nguyên dương phân biệt, trong đó mỗi số có giá trị không vượt quá 100. CMR có thể chọn ra 4 số phân biệt a,b,c,d sao cho \(a^2+b^2+c^2+d^2\) là tổng của 3 số chính phương khác 0
Cho hàm số y = − x + 1 2 x − 1 có đồ thị là (C), đường thẳng d : y = x + m . Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k 1 + k 2 đạt giá trị lớn nhất.
A. m = -1
B. m = -2
C. m = 3
D. m = -5
Từ bốn chữ số a,b,c,d khác nhau và khác o, ta lập số tự nhiên lớn nhất có 4 chữ số khác và số tự nhiên nhỏ nhất có 4 chữ số khác nhau. Tổng của hai số này bằng 15664. Tổng a+b+c+d là
abcd + dcba = 15664
1000*a+100*b+10*c+d+1000*d+100*c+10*b+a=15664
1001*(a+d)+110*(b+c)=15664
Mà 110*(b+c) có tận cùng là 0
Nên 1001*(a+d) có tận cùng là 4
Nên a + d có tận cùng là 4
1001 * 4 = 4004 ( loại )
1001 * 14 = 14014 ( nhận )
Vậy a+c=14
Vậy a = 9 ; d = 5
14014+110*(b+c)=15664
110*(b+c)=1650
b+c=1650:110
b+c=15
Vậy a + b + c + d = 14 + 15 = 29
Câu 1. Kết quả của a – (b + c - d) là
A. a + b + c - d B. a - b - c - d
C. a - b + c - d D. a - b - c + d
Câu 2. Nếu một tổng có ba số hạng, trong đó có 2 số hạng chia hết cho 7 và số hạng còn lại không chia hết cho 7 thì tổng đó
A. chia hết cho 7. B. không chia hết cho 7.
C. không kết luận được. D. chia hết cho ước của 7.
Câu 3. Trong các số sau số nào chia hết cho 9 nhưng không chia hết cho 5?
A. 315 B. 423 C. 720 D. 263
Câu 4. Trong các số tự nhiên sau số nào là số nguyên tố?
A.51 B. 39 C.75 D.83
Câu 5. Tìm tập các ước nguyên của 5.
A. Ư(5) = {1; 5} B. Ư(5) = {-1; -5}
C. Ư(5) ={1; -1; 5; -5} D. Ư(5) = {0; 5; 10; …}
Câu 6. Trong lục giác đều mỗi góc có số đo bằng
A. 600 B. 900 C. 1200 D. 300
Câu 7. Trong các hình sau, hình nào không có tâm đối xứng?
A. Hình tròn. B. Tam giác đều. C. Hình lục giác đều. D. Hình vuông.
Câu 8. Tập hợp P các số tự nhiên không vượt quá 8 có thể viết là
A. P = {x Î N | x < 9 } B. P = {x Î N | x ![]() 9}
9}
C. P = { x Î N | x ![]() 8 } D. P = { x Î N | x < 8 }
8 } D. P = { x Î N | x < 8 }
Câu 9. Cho đoạn thẳng MN dài 18cm. Biết O là tâm đối xứng của MN. Tính ON.
A. 9cm B. 8cm C. 18cm D. 6cm
Câu 10. Hình thang cân có độ dài hai đáy lần lượt bằng 6 cm, 8 cm và chiều cao bằng 4 cm thì diện tích hình thang cân đó là:
A. 14 cm2 B. 48 cm2 C. 28 cm2 D. 56 cm2
Câu 11. Số 828 chia hết cho các số nào sau đây?
A. 2 và 9 B. 2 và 5 C. 3 và 5 D. 5 và 9
Câu 12. Trong các số tự nhiên sau số nào là số nguyên tố?
A.26 B. 81 C.11 D.21
Câu 13. Trong tam giác đều mỗi góc có số đo bằng
A. 600 B. 450 C. 900 D. 300
Câu 14. Hình nào dưới đây có vô số trục đối xứng?
A. Hình lục giác đều B. Hình vuông C. Hình chữ nhật D. Hình tròn
Câu 15. Tập hợp P các số tự nhiên nhỏ hơn hoặc bằng 8 có thể viết là
A. P ={x Î N | x < 8 } B. P ={x Î N | x ![]() 9}
9}
C. P ={ x Î N | x ![]() 8 } D. P ={ x Î N | x < 9 }
8 } D. P ={ x Î N | x < 9 }
Câu 16. Tìm các số nguyên x thỏa mãn – 12 < x < 13. Có bao nhiêu số nguyên như vậy?
A. 23; B. 24; C. 25; D. 26.
Câu 17. Cho hình thoi, biết độ dài hai đường chéo là 6cm và 8cm thì diện tích hình thoi là
A.14 cm2 B. 24 cm2 C. 28 cm2 D. 48 cm2