Tính giá trị biểu thức
a, 2x3+5 tại x thỏa mãn x2-x=0
các bn giúp mik nhé!!!
Những câu hỏi liên quan
tính giá trị của biểu thức p= 2x3+5 tại x thỏa mãn x2-x=0
Xem chi tiết
\(x^2-x=0\Leftrightarrow x\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow P=2.0^3+5=5\)
- Với \(x=1\Rightarrow P=2.1^3+5=7\)
Đúng 0
Bình luận (0)
28 tháng 10 2021 lúc 14:33
Bài 8 : Tìm GTNN của biểu thức:
F= ( x - 1 )2 + ( x - 3 )2
Bài 9 : Tìm GTLN của biểu thức:
A= 4 - x2 + 2x
B= 10x - 23 - x2
C= -x2 + 6x
a) Rút gọn A
b) Với giá trị x;y nguyên dương nào thỏa mãn x + 2y = 14 nhận giá trị nguyên dương.
Mn giúp mik nhé! mik ko làm đc mấy bài này.
Bài 8:
\(F=x^2-2x+1+x^2-6x+9=2x^2-8x+10\\ F=2\left(x^2-4x+4\right)+2=2\left(x-2\right)^2+2\ge2\\ F_{min}=2\Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
Bài 9:
\(A=-x^2+2x-1+5=-\left(x-1\right)^2+5\le5\\ A_{max}=5\Leftrightarrow x=1\\ B=-x^2+10x-25+2=-\left(x-5\right)^2+2\le2\\ B_{max}=2\Leftrightarrow x=5\\ C=-x^2+6x-9+9=-\left(x-3\right)^2+9\le9\\ C_{max}=9\Leftrightarrow x=3\)
Đúng 1
Bình luận (0)
giúp với ạBài 1:Rút gọn biểu thứca)A(x+y)2 - (x-y)2b)B(x+y)2 - 2(x+y)(x-y)+(x-y)2c)(x2 + x +1)(x2 -x+1)(x2 -1)d)(a+b-c)2 + (a-b+c)2 - 2(b-c)2Bài 2: Cho các số thực x,y thỏa mãn điều kiện x+y3; x2 +y2 17. Tính giá trị biểu thức x3 +y3
Đọc tiếp
giúp với ạ
Bài 1:Rút gọn biểu thức
a)A=(x+y)2 - (x-y)2
b)B=(x+y)2 - 2(x+y)(x-y)+(x-y)2
c)(x2 + x +1)(x2 -x+1)(x2 -1)
d)(a+b-c)2 + (a-b+c)2 - 2(b-c)2
Bài 2: Cho các số thực x,y thỏa mãn điều kiện x+y=3; x2 +y2 =17. Tính giá trị biểu thức x3 +y3
B1
a, \(=>A=\left(x+y+x-y\right)\left(x+y-x+y\right)=2x.2y=4xy\)
b, \(=>B=\left[\left(x+y\right)-\left(x-y\right)\right]^2=\left[x+y-x+y\right]^2=\left[2y\right]^2=4y^2\)
c,\(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^2-1\right)\)
\(=\)\(\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)=\left(x^3+1^3\right)\left(x^3-1^3\right)=x^6-1\)
d, \(\left(a+b-c\right)^2+\left(a-b+c\right)^2-2\left(b-c\right)^2\)
\(=\left(a+b-c\right)^2-\left(b-c\right)^2+\left(a-b+c\right)^2-\left(b-c\right)^2\)
\(=\left(a+b-c+b-c\right)\left(a+b-c-b+c\right)\)
\(+\left(a-b+c+b-c\right)\left(a-b+c-b+c\right)\)
\(=a\left(a+2b-2c\right)+a\left(a-2b\right)\)
\(=a\left(a+2b-2c+a-2b\right)=a\left(2a-2c\right)=2a^2-2ac\)
B2:
\(\)\(x+y=3=>\left(x+y\right)^2=9=>x^2+2xy+y^2=9\)
\(=>xy=\dfrac{9-\left(x^2+y^2\right)}{2}=\dfrac{9-\left(17\right)}{2}=-4\)
\(=>x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=3\left(17+4\right)=63\)
Đúng 1
Bình luận (0)
Bài 1:
a) Ta có: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-x^2+2xy+y^2\)
=4xy
b) Ta có: \(\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)^2\)
\(=\left(2y\right)^2=4y^2\)
c) Ta có: \(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^2-1\right)\)
\(=\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)\left(x^2-x+1\right)\)
\(=\left(x^3-1\right)\left(x^3+1\right)\)
\(=x^6-1\)
d) Ta có: \(\left(a+b-c\right)^2+\left(a+b+c\right)^2-2\left(b-c\right)^2\)
\(=\left(a+b-c\right)^2-\left(b-c\right)^2+\left(a+b+c\right)^2-\left(b-c\right)^2\)
\(=\left(a+b-c-b+c\right)\left(a+b-c+b-c\right)+\left(a+b+c-b+c\right)\left(a+b+c+b-c\right)\)
\(=a\cdot\left(a+2b-2c\right)+\left(a+2c\right)\left(a-2b\right)\)
\(=a^2+2ab-2ac+a^2-2ab+2ac-4bc\)
\(=2a^2-4bc\)
Đúng 1
Bình luận (0)
Bài 2:
Ta có: x+y=3
nên \(\left(x+y\right)^2=9\)
\(\Leftrightarrow2xy+17=9\)
\(\Leftrightarrow2xy=-8\)
hay xy=-4
Ta có: \(x^3+y^3\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=3^3-3\cdot\left(-4\right)\cdot3\)
\(=27+36=63\)
Đúng 1
Bình luận (0)
1) rút gọn biểu thức
a) (x2- 5)-(x+7)(x-7)
b)(2x+3y)2+(3x-2y)2-2(2x+3y)(2x+3y93x-2y)
2) tìm giá trị biểu thức
A= x3+3x2+3x+1 tại x = 99
mn giúp mình lẹ đi đang gấp
Cho
x
,
y
∈
R
thỏa mãn điều kiện
2
y
≥
x
2
và
y
≤
-
2
x
3
+
3
x
Tìm giá trị lớn nhất của biểu thức
P
x
2
+
y
2
A. 5 B. 4 C. 3 D. 2
Đọc tiếp
Cho x , y ∈ R thỏa mãn điều kiện 2 y ≥ x 2 và y ≤ - 2 x 3 + 3 x Tìm giá trị lớn nhất của biểu thức P = x 2 + y 2
A. 5
B. 4
C. 3
D. 2
Từ giả thiết bài toán suy ra
y ≥ 0 x 2 2 ≤ - 2 x 2 + 3 x ⇔ y ≥ 0 5 x 2 - 6 x ≤ 0 ⇔ y ≥ 0 0 ≤ x ≤ 6 5
Ta có
x 2 + y 2 ≤ x 2 + - 2 x 2 + 3 x 2 = 4 x 4 - 12 x 3 + 10 x 2
Ta có f ' x = 4 x x - 1 x - 5
f ' x = 0 x = 0 x = 1 x = 5 So điều kiện, chọn x = 0 ; x = 1 ; f(0); f(1) = 2; f 6 5 = 1224 625
Vậy m a x P = 2
Đáp án D
Đúng 0
Bình luận (0)
Cho x,y0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3
y
-...
Đọc tiếp
Cho x,y>0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Ta có:
x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2
Do x,y>0 nên ⇔ x 2 + 3 x thay vào (2) ta được:
2 x + 3 . x 2 + 3 x - 14 ≤ 0
⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0
⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5
Thay y = x 2 + 3 x vào P ta được:
P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x
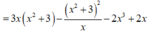
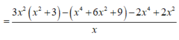
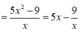
P ' = 5 + 9 x 2 > 0 với mọi x nên hàm số P=P(x) đồng biến trên 1 ; 9 5
Vậy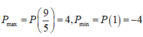 
Tổng 
.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho x,y 0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
2
y
-...
Đọc tiếp
Cho x,y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 2 y - 14 ≤ 0 .Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
A. 4.
B. 8.
C. 12.
D. 0.
Cho
x
,
y
0
và thỏa mãn
x
2
−
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 − x y + 3 = 0 2 x + 3 y − 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y − x y 2 − 2 x 3 + 2 x ?
A. 4
B. 8
C. 12
D. 0
Cho
x
,
y
0
và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Đáp án B
Phương pháp:
- Rút y từ phương trình đầu, thay vào bất phương trình sau tìm điều kiện của x .
- Thay y ở trên vào biểu thức P đưa về biến x .
- Sử dụng phương pháp hàm số đánh giá P tìm GTLN, GTNN.
Đúng 0
Bình luận (0)