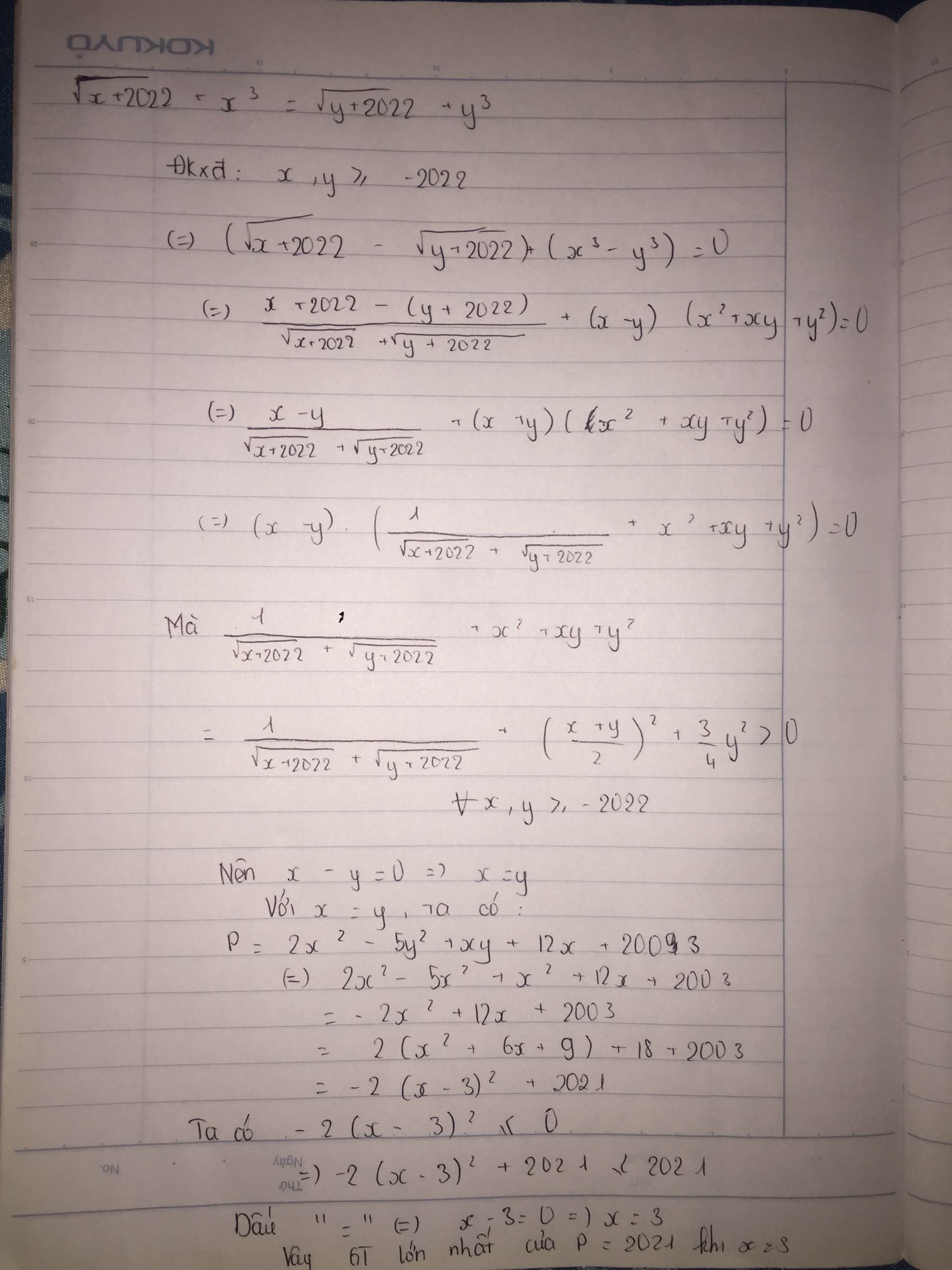cho \(\sqrt{x+2022}+x^3=\sqrt{y+2022}+y^3\). Tìm max P=\(2x^2-5y^2+xy+12x+2023\)
Những câu hỏi liên quan
Cho các số x,y thỏa mãn\(\sqrt{x+2}-y^3=\sqrt{y+2}-x^3\).Tìm GTNN của biểu thức A=\(x^2-xy+y^2+2x+2022\)
7 tháng 2 2022 lúc 9:34
Cần gấp !!!
Cho \(\sqrt{x+2020}+x^3=\sqrt{y+2020}+y^3\) Tìm giá trị lớn nhất \(P=2x^2-5y^2+xy+12x+2003\)
( x + 3 )2022 + ( \(\sqrt{y-2}\) - 1 )2023 = 0
mình cần gấp mong mọi người giúp ạ!!
\(\left(x+3\right)^{2022}+\left(\sqrt{y-2}-1\right)^{2023}=0\) \(\left(ĐKXĐ: y\ge2\right)\)
Xét \(\left(x+3\right)^{2022}\ge0\forall x\)
\(\Rightarrow\left(\sqrt{y-2}-1\right)^{2023}\le0\)
\(\Leftrightarrow\sqrt{y-2}-1\le0\)
\(\Leftrightarrow\sqrt{y-2}\le1\)
\(\Leftrightarrow y-2\le1\)
\(\Rightarrow y\le3\)
\(\Rightarrow2\le y\le3\) mà \(y\in Z\)
\(\Rightarrow\left\{{}\begin{matrix}y=2\Leftrightarrow x=-2\\y=3\Leftrightarrow x=-3\end{matrix}\right.\)
Đúng 2
Bình luận (1)
23 tháng 12 2022 lúc 20:03
a) cho C = 3 - \(3^2+3^3-3^4+3^5-3^6+...+3^{23}-3^{24}\), chứng minh rằng C \(⋮\) 420
b) tìm x và y biết \(\left(x+1\right)^{2022}+\left(\sqrt{y-1}\right)^{2023}=0\)
Cho các số a,b,c,d khác 0 và x,y,z,t thỏa mãn:
x^2022+y^2022+z^2022+t^2022/a^2+b^2+c^2+d^2=x^2022/a^2+y^2022/b^2+z^2022/c^2+t^2022/d^2.
Tính T=x^2023+y^2023+z^2023+t^2023
cho( x-1)^2022+/y+1/=0 tính giá trị biểu thức p=x^2023.y^2022/(2x+y)^2022+2023
ai giúp mình với
olm sẽ hướng dẫn em làm bài này như sau:
Bước 1: em giải phương trình tìm; \(x\); y
Bước 2: thay\(x;y\) vào P
(\(x-1\))2022 + |y + 1| = 0
Vì (\(x-1\))2022 ≥ 0 ∀ \(x\); |y + 1| ≥ 0 ∀ y
⇒ (\(x\) - 1)2022 + |y + 1| = 0
⇔ \(\left\{{}\begin{matrix}\left(x-1\right)^{2022}=0\\y+1=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\) (1)
Thay (1) vào P ta có:
12023.(-1)2022 : )(2.1- 1)2022 + 2023
= 1 + 2023
= 2024
Đúng 0
Bình luận (0)
mọi người hãy trình bầy rõ ra nhé
em ko hiểu nên nếu nói tắt sẽ ko thể tiếp thu
Đúng 0
Bình luận (0)
13 tháng 6 2023 lúc 13:57
Tìm x và y biết (x+1)\(^{2022}\)+(\(\sqrt{y-1}\))\(^{2023}\)
mình cần gấp giúp mình với!!!!☹
A = (\(x\) + 1)2022 + (\(\sqrt{y-1}\))2023 đkxđ : y - 1 ≥ 0 ⇒ y ≥ 1
⇔ (\(x\) + 1)2022 + (\(\sqrt{y-1}\))2023 = 0
vì (\(x\) + 1)2022 ≥ 0; \(\sqrt{y-1}\) ≥ 0 ⇒ (\(\sqrt{y-1}\))2023 ≥ 0
Nên A = 0 ⇔ \(\left\{{}\begin{matrix}x+1=0\\y-1=0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Nghiệm của A là: \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
tìm cặp số thực x,y thỏa mãn điều kiện:
\(\sqrt{x-1}\)+\(\sqrt{3-x}=y^2+2\sqrt{2020}y+2022\).
\(\left(\sqrt{x-1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(x-1+3-x\right)=4\\ \Leftrightarrow\sqrt{x-1}+\sqrt{3-x}\le2\\ y^2+2\sqrt{2020}y+2022=\left(y^2+2y\sqrt{2020}+2020\right)+2\\ =\left(y+\sqrt{2020}\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-1=3-x\\y+\sqrt{2020}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\sqrt{2020}\end{matrix}\right.\)
Vậy ...
Đúng 2
Bình luận (0)
ĐKXĐ: \(3\ge x\ge1\)
Áp dụng BĐT Bunhiacopski:
\(1\sqrt{x-1}+1\sqrt{3-x}\le\sqrt{\left(1^2+1^2\right)\left(x-1+3-x\right)}=\sqrt{2.2}=2\)
Mặt khác: \(y^2+2\sqrt{2020}y+2022=\left(y+\sqrt{2020}\right)^2+2\ge2\)
Nên để thõa mãn yêu cầu bài toán thì
\(\left\{{}\begin{matrix}\sqrt{x-1}=\sqrt{3-x}\\y+\sqrt{2020}=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\left(tm\right)\\y=-\sqrt{2020}\end{matrix}\right.\)
Đúng 2
Bình luận (1)
2 tháng 11 2023 lúc 12:34
Tìm cặp số thực x, y thỏa mãn điều kiện \(\sqrt{x-1} + \sqrt{3-x} = y^2 + 2\sqrt{2020y} +2022\)
Lời giải:
Ta có:\(y^2+2\sqrt{2020}y+2022=(y^2+2\sqrt{2020}y+2020)+2=(y+\sqrt{2020})^2+2\geq 2(1)\)
Áp dụng BĐT Bunhiacopxky:
$(\sqrt{x-1}+\sqrt{3-x})^2\leq (x-1+3-x)(1+1)=4$
$\Rightarrow \sqrt{x-1}+\sqrt{3-x}\leq 2(2)$
Từ $(1); (2)\Rightarrow \sqrt{x-1}+\sqrt{3-x}\leq 2\leq y^2+2\sqrt{2020}y+2022$
Dấu "=" xảy ra khi mà: \(\left\{\begin{matrix} \frac{x-1}{1}=\frac{3-x}{1}\\ y+\sqrt{2020}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=2\\ y=-\sqrt{2020}\end{matrix}\right.\)
Đúng 0
Bình luận (0)