Giúp e vs ạ PART C: LEXICAL & GRAMMAR (30 poimts) Question I. Choose the best answer to complete each of the following sentences. (10 pts) 1. We need a password to get to the computer system. A. access B. information C. programs D. connection 2. It's 7 years since we A. talked to last Daisy B. have talked to Daisy C. last talked to Daisy D. last talked Daisy 3. Tim was the last person B. left the class yesterday. A. to leave C. who leaves D. leaving 4. Normally he is rather A. reserved B. sociable but sometimes he talks freely about himself C. serious D. peaceful .............in the southern part of the country is very rich and fertile. 5. The C. ground 6. As she didn't understand his question she merely gave him a ..look. A. earth B. land B. blank 7. Everyone can join our club, A. clear D. useless A.not mention B. in case of C. in place of D. regardless of C. simple age and sex. 8. I hope the weather improves, A. However B. Although D. soil we'll have to cancel the picnic. C. Therefore D. Otherwise 9. Not only... but she also plays the guitar and compose songs. A. does she sing B. she sings D. she sing C. if she sings 10. I don't usually like staying at hotels but last summer we spent a few days at hotel by.. sea. very nice A. a; the B. a; Ø C. the; a D. Ø the

Những câu hỏi liên quan
Giải giúp e part 5a vs ạ

I. Find the word which has a different sound in the part underlined
1. A. better B. prefer C. teacher D. worker
mn giúp e vs ạ
A.c giúp e vs ạ. E đang cần gấp ạ. C,mơn trc ạ 


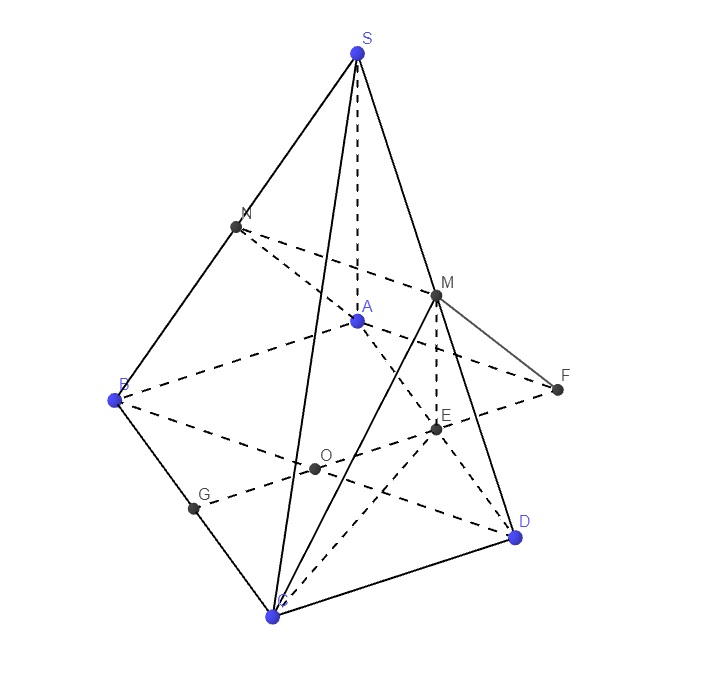
giúp e câu c, e vs ạ
c.
Gọi E là trung điểm AD \(\Rightarrow EM\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}EM=\dfrac{1}{2}SA=a\\EM||SA\Rightarrow EM\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow EC\) là hình chiếu vuông góc của CM lên (ABCD)
\(\Rightarrow\widehat{MCE}\) là góc giữa SM và (ABCD)
\(ED=\dfrac{1}{2}AD=a\Rightarrow EC=\sqrt{CD^2+ED^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{MCE}=\dfrac{EM}{EC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{MCE}=...\)
e.
Gọi O là trung điểm BD, qua A kẻ đường thẳng song song BD cắt OE kéo dài tại F
\(\Rightarrow ABOF\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\left\{{}\begin{matrix}AF=OB=\dfrac{1}{2}BD\\AF||BD\end{matrix}\right.\)
Lại có MN là đường trung bình tam giác SBD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}MN=AF\\MN||AF\end{matrix}\right.\) \(\Rightarrow ANMF\) là hình bình hành
\(\Rightarrow AN||MF\Rightarrow\left(AN;CM\right)=\left(AN;MF\right)=\widehat{CMF}\) nếu nó ko tù hoặc bằng góc bù của nó nếu \(\widehat{CMF}\) là góc tù
Ta có: \(MF=AN=\dfrac{a\sqrt{5}}{2}\) ; \(CM=\sqrt{CE^2+EM^2}=a\sqrt{3}\)
ABOF là hình bình hành nên AODF cũng là hình bình hành \(\Rightarrow E\) là tâm hình bình hành
\(\Rightarrow EF=OF=\dfrac{AB}{2}=\dfrac{a}{2}\)
Gọi G là giao điểm OE và BC \(\Rightarrow FG=EG+EF=a+\dfrac{a}{2}=\dfrac{3a}{2}\)
\(\Rightarrow CF=\sqrt{FG^2+CG^2}=\dfrac{a\sqrt{13}}{2}\)
ĐỊnh lý hàm cos:
\(cos\widehat{CMF}=\dfrac{CM^2+MF^2-CF^2}{2CM.MF}=\dfrac{\sqrt{15}}{15}\Rightarrow\widehat{CMF}\)
Đúng 1
Bình luận (2)
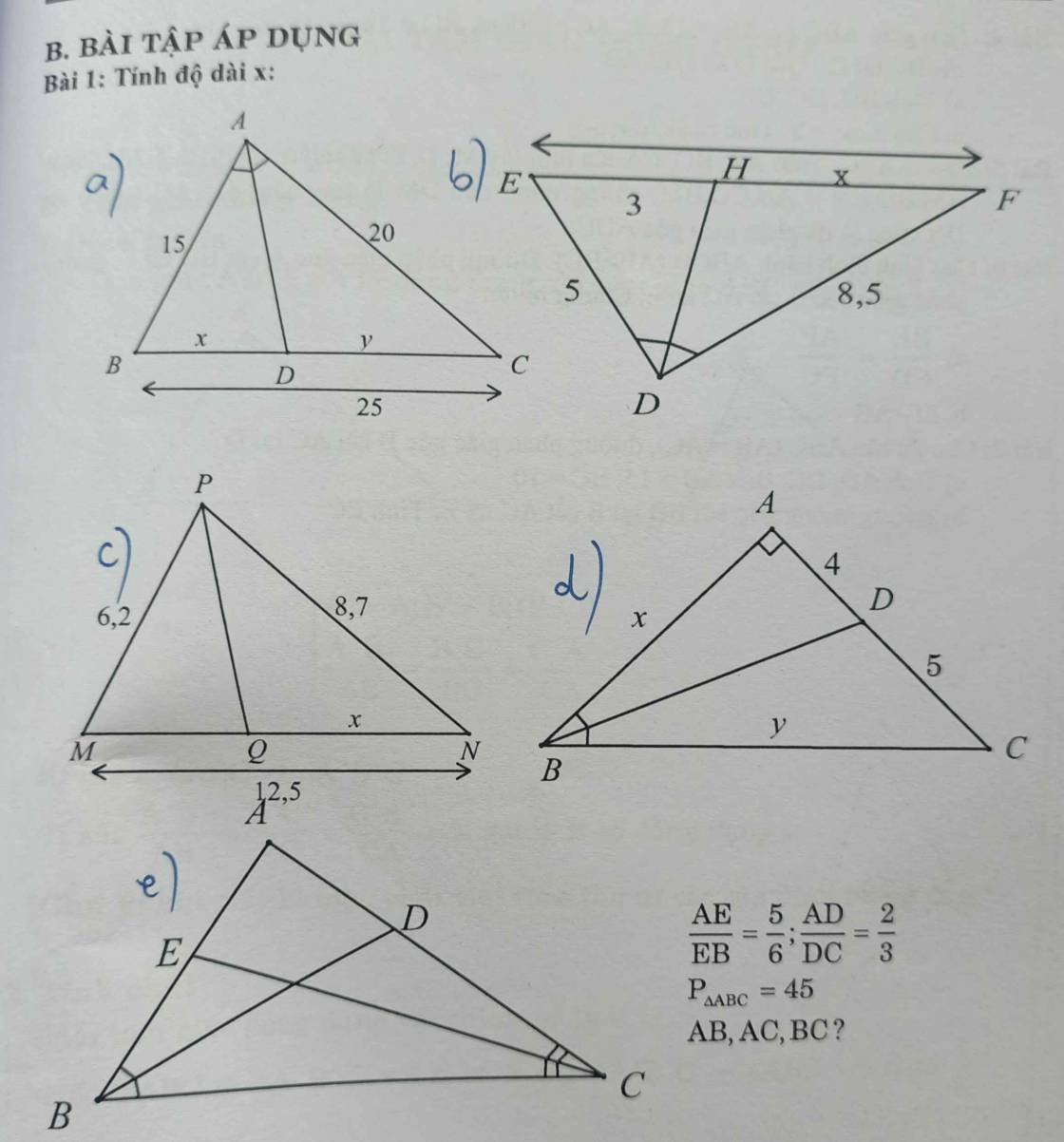 giúp e c,d,e vs ạ
giúp e c,d,e vs ạ
c: Xét ΔPMN có PQ là đường phân giác
nên \(\dfrac{MQ}{MP}=\dfrac{NQ}{PN}\)
=>\(\dfrac{MQ}{6,2}=\dfrac{QN}{8,7}\)
mà MQ+QN=MN=12,5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MQ}{6,2}=\dfrac{QN}{8,7}=\dfrac{MQ+QN}{6,2+8,7}=\dfrac{12.5}{14.9}=\dfrac{125}{149}\)
=>\(\dfrac{x}{8,7}=\dfrac{125}{149}\)
=>\(x=\dfrac{125}{149}\cdot\dfrac{87}{10}=\dfrac{87\cdot25}{2\cdot149}=\dfrac{2175}{298}\)
d: Xét ΔBAC có BD là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AD}{DC}=\dfrac{4}{5}\)
=>\(\dfrac{BA}{4}=\dfrac{BC}{5}=k\)
=>BA=4k; BC=5k
=>x=4k; y=5k
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2-AB^2=AC^2\)
=>\(\left(5k\right)^2-\left(4k\right)^2=9^2\)
=>\(9k^2=81\)
=>\(k^2=9\)
=>k=3
=>\(x=4\cdot3=12;y=5\cdot3=15\)
e: Xét ΔBAC có BD là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AD}{DC}=\dfrac{2}{3}\)
=>\(\dfrac{BA}{2}=\dfrac{BC}{3}\)
=>\(\dfrac{BA}{4}=\dfrac{BC}{6}\)
Xét ΔCAB có CE là phân giác
nên \(\dfrac{CA}{CB}=\dfrac{AE}{EB}=\dfrac{5}{6}\)
=>\(\dfrac{CA}{5}=\dfrac{CB}{6}\)
=>\(\dfrac{BA}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}\)
mà \(BA+AC+BC=P_{ABC}\cdot2=90\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BA}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}=\dfrac{AB+AC+BC}{4+5+6}=\dfrac{90}{15}=6\)
=>\(AB=4\cdot6=24\left(cm\right);AC=5\cdot6=30\left(cm\right);BC=6\cdot6=36\left(cm\right)\)
Đúng 3
Bình luận (1)
giúp e câu a,b,c,e vs ạ
Những câu đã đăng rồi thì em hạn chế đăng lại nhé.
Đúng 1
Bình luận (1)
a: \(=\dfrac{\left(4\sqrt{3}-5\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}\right)}{\sqrt{3}}\)
=4-5+1/2*4
=-1+2
=1
b: \(=\left|2-\sqrt{5}\right|-\left|\sqrt{5}+1\right|\)
\(=\sqrt{5}-2-\sqrt{5}-1=-3\)
c: \(=\dfrac{3\left(\sqrt{7}+2\right)}{3}-\dfrac{4\left(3-\sqrt{7}\right)}{2}\)
\(=\sqrt{7}+2-2\left(3-\sqrt{7}\right)\)
\(=\sqrt{7}+2-6+2\sqrt{7}=3\sqrt{7}-4\)
d: \(=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)
\(=3\sqrt{2a}-3a\cdot\sqrt{2a}+2\sqrt{2a}-2\sqrt{2a}\)
\(=\sqrt{2a}\left(3-3a\right)\)
e: \(=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{2\left(\sqrt{3}+1\right)}{2}\)
\(=\sqrt{3}-\sqrt{3}-1=-1\)
Đúng 0
Bình luận (0)
giúp e câu a,b,c,e vs ạ
a) \(A=\left(2\sqrt{12}-\sqrt{75}+\dfrac{1}{2}\sqrt{48}\right):\sqrt{3}\)
\(A=\left(4\sqrt{3}-5\sqrt{3}+2\sqrt{3}\right):\sqrt{3}\)
\(A=\sqrt{3}:\sqrt{3}\)
\(A=1\)
b) \(B=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(B=\left|2-\sqrt{5}\right|-\left|\sqrt{5}+1\right|\)
\(B=-2+\sqrt{5}-\sqrt{5}-1\)
\(B=-3\)
c) \(C=\dfrac{3}{\sqrt{7}-2}-\dfrac{4}{3+\sqrt{7}}\)
\(C=\dfrac{3\left(\sqrt{7}+2\right)}{\left(\sqrt{7}-2\right)\left(\sqrt{7}+2\right)}-\dfrac{4\left(3-\sqrt{7}\right)}{\left(3+\sqrt{7}\right)\left(3-\sqrt{7}\right)}\)
\(C=\dfrac{3\left(\sqrt{7}+2\right)}{3}-\dfrac{4\left(3-\sqrt{7}\right)}{2}\)
\(C=\sqrt{7}+2-2\left(3-\sqrt{7}\right)\)
\(C=\sqrt{7}+2-6+2\sqrt{7}\)
\(C=3\sqrt{7}-4\)
d) \(D=3\sqrt{2a}-\sqrt{18a^3}+4\sqrt{\dfrac{a}{2}}-\dfrac{1}{4}\sqrt{128a}\)
\(D=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)
\(D=5\sqrt{2a}-3a\sqrt{2a}-2\sqrt{2a}\)
\(D=3\sqrt{2a}-3a\sqrt{2a}\)
e) \(E=\dfrac{3+\sqrt{3}}{\sqrt{3}}-\dfrac{2}{\sqrt{3}-1}\)
\(E=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(E=\left(\sqrt{3}+1\right)-\dfrac{2\left(\sqrt{3}+1\right)}{2}\)
\(E=\left(\sqrt{3}+1\right)-\left(\sqrt{3}+1\right)\)
\(E=0\)
Đúng 3
Bình luận (0)
Lời giải:
a.
\(A=2\sqrt{\frac{12}{3}}-\sqrt{\frac{75}{3}}+\frac{1}{2}\sqrt{\frac{48}{3}}=2\sqrt{4}-\sqrt{25}+\frac{1}{2}\sqrt{16}\)
\(2.2-5+\frac{1}{2}.4=1\)
b.
\(B=|2-\sqrt{5}|-|\sqrt{5}+1|=\sqrt{5}-2-(\sqrt{5}+1)=-3\)
c.
\(C=\frac{3(\sqrt{7}+2)}{(\sqrt{7}-2)(\sqrt{7}+2)}-\frac{4(3-\sqrt{7})}{(3+\sqrt{7})(3-\sqrt{7})}\)
\(=\frac{3(\sqrt{7}+2)}{7-2^2}-\frac{4(3-\sqrt{7})}{3^2-7}\)
\(=\frac{3(\sqrt{7}+2)}{3}-\frac{4(3-\sqrt{7})}{2}=\sqrt{7}+2-2(3-\sqrt{7})=-4+3\sqrt{7}\)
e.
\(E=\frac{\sqrt{3}(\sqrt{3}+1)}{\sqrt{3}}-\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\sqrt{3}+1-\frac{2(\sqrt{3}+1)}{3-1^2}=(\sqrt{3}+1)-(\sqrt{3}+1)=0\)
Đúng 1
Bình luận (0)
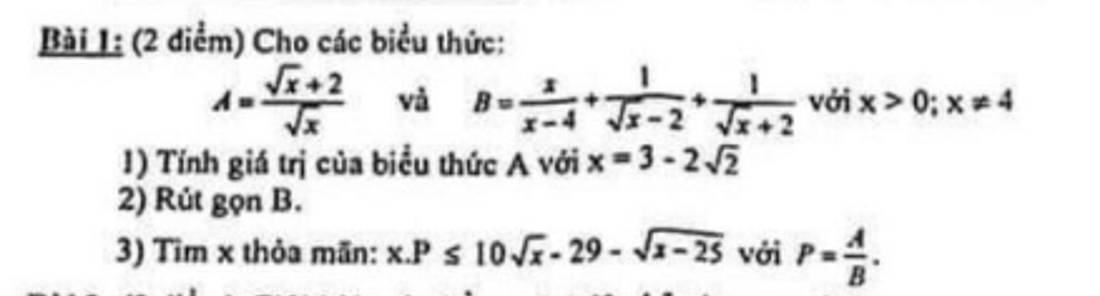
mn giúp e phần c vs ạ
e cảm ơnn
1: Khi x=3-2 căn 2 thì \(A=\dfrac{\sqrt{2}-1+2}{\sqrt{2}-1}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}=3+2\sqrt{2}\)
2: \(B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3: \(P=A:B=\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{x-4}{x}\)
\(x\cdot P< =10\sqrt{x}-29-\sqrt{x-25}\)
=>\(x-4< =10\sqrt{x}-29-\sqrt{x-25}\)
\(\Leftrightarrow x-4-10\sqrt{x}+29< =-\sqrt{x-25}\)
=>\(x-10\sqrt{x}+25< =-\sqrt{x-25}\)
=>(căn x-5)^2<=-căn x-25
=>x-25=0
=>x=25
Đúng 0
Bình luận (1)
Giải giúp e ý c vs ạ