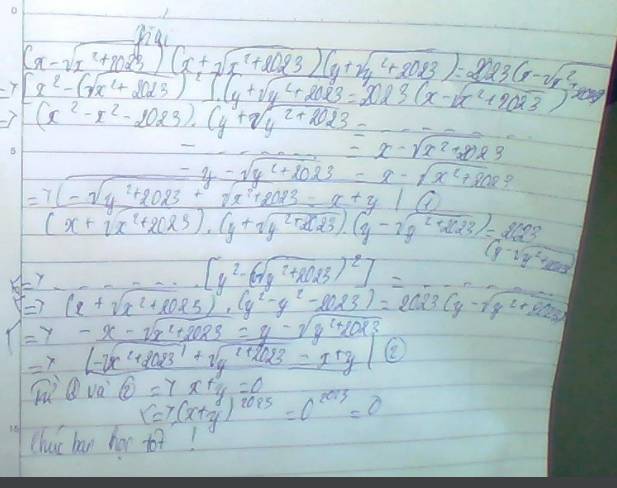Giải phương trình sau \(\sqrt{2023-\sqrt{x}}=2023-x\)

Những câu hỏi liên quan
Giải phương trình sau: \(\sqrt{2023-\sqrt{x}}=2023-x\)
giúp mik vs ạ, mik cảm ơn :>
\(\sqrt{2023-\sqrt{x}}=2023-x\left(ĐK:x\ge0\right)\)
Đặt \(t=\sqrt{x}\left(t\le2023\right)\)
Pt trở thành : \(\sqrt{2023-t}=2023-t^2\)
\(\Leftrightarrow2023-t=\left(2023-t^2\right)^2\)
\(\Leftrightarrow t^4-4046t+4092529=2023-t\)
\(\Leftrightarrow t^4-4045+4090506=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2023\left(n\right)\\t=2022\left(n\right)\end{matrix}\right.\)
+) Với \(t=2023\Rightarrow x^2=2023\Rightarrow x=\pm17\sqrt{7}\)
+) Với \(t=2022\Rightarrow x^2=2022\Leftrightarrow x=\pm\sqrt{2022}\)
Vì \(x\ge0\) \(\Rightarrow x\in\left\{17\sqrt{7};\sqrt{2022}\right\}\)
Vậy \(S=\left\{17\sqrt{7};\sqrt{2022}\right\}\)
Đúng 1
Bình luận (4)
Bài 4. (1,0 điểm)
Giải phương trình $\sqrt{x+3} . x^4=2 x^4-2023 x+2023$.
Bài 4: \(\sqrt{x+3}\cdot x^4=2x^4-2023x+2023\) (ĐK: x ≥ -3)
⇔ \(x^4\left(\sqrt{x+3}-2\right)+2023\left(x-1\right)=0\)
⇔ \(x^4\left(\dfrac{x-1}{\sqrt{x+3}+2}\right)+2023\left(x-1\right)=0\)
⇔ \(\left(x-1\right)\left(\dfrac{x^4}{\sqrt{x+3}+2}+2023\right)=0\)
⇒ \(x-1=0\)
⇔ \(x=1\left(TM\right)\)
Vậy S ∈ {1}
Đúng 0
Bình luận (0)
Giai phương trình sau: \(\sqrt{2020-x}+\sqrt{2023-x}+\sqrt{2028-x}=6\)
\(\sqrt{2020-x}+\sqrt{2023-x}+\sqrt{2028-x}=6\)\(\left(x\le2020\right)\)
\(\Leftrightarrow\sqrt{2020-x}-1+\sqrt{2023-x}-2+\sqrt{2020-x}-3=0\)
\(\Leftrightarrow\frac{\left(\sqrt{2020-x}-1\right)\left(\sqrt{2020-x}+1\right)}{\sqrt{2020-x}+1}\) \(+\frac{\left(\sqrt{2023-x}-2\right)\left(\sqrt{2023-x}+2\right)}{\sqrt{2023-x}+2}\)\(+\frac{\left(\sqrt{2028-x}-3\right)\left(\sqrt{2028-x}+3\right)}{\left(\sqrt{2028-x}+3\right)}\)=0
\(\Leftrightarrow\frac{2019-x}{\sqrt{2020-x}+1}+\frac{2019-x}{\sqrt{2023-x}+2}+\frac{2019-x}{\left(\sqrt{2028-x}+3\right)}\)=0
\(\Leftrightarrow\left(2019-x\right)\left(\frac{1}{\sqrt{2020-x}+1}+\frac{1}{\sqrt{2023-x}+2}+\frac{1}{\sqrt{2028-x}+3}\right)\)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=2019\left(tm\right)\\\frac{1}{\sqrt{2020-x}+1}+\frac{1}{\sqrt{2023-x}+2}+\frac{1}{\sqrt{2028-x}+3}=0\left(2\right)\end{matrix}\right.\)
vì \(\sqrt{2020-x}\ge0\Rightarrow\frac{1}{\sqrt{2020-x}+1}>0\)
cmtt: \(\frac{1}{\sqrt[]{2023-x}+2}>0\)
\(\frac{1}{\sqrt{2028-x}+3}>0\)
=>\(\frac{1}{\sqrt{2020-x}+1}+\frac{1}{\sqrt{2023-x}+2}+\frac{1}{\sqrt{2028-x}+3}>0\)(3)
từ (2) và (3)=> vô lý
vậy x=2019 là nghiệm của phương trình
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023
\)
Tính (x+y)2023
Helpppppppppp
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. Trước tiên, ta mở đuôi công thức:(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)Từ phép nhân đầu tiên, ta có:(x+y)(x+y) = x^2 + 2xy + y^2Tiếp tục nhân với (x+y), ta có:(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3Lặp lại quá trình này 2020 lần nữa, ta có:(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4Tiếp tục nhân với (x+y), ta có:(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
Đúng 0
Bình luận (2)
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức.
Trước tiên, ta mở đuôi công thức:
(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)
Từ phép nhân đầu tiên, ta có:
(x+y)(x+y) = x^2 + 2xy + y^2
Tiếp tục nhân với (x+y), ta có:
(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3
Lặp lại quá trình này 2020 lần nữa, ta có:
(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4
Tiếp tục nhân với (x+y), ta có:
(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
Đúng 0
Bình luận (0)
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023\)
Tính (x+y)2023
Help me plsss
Giải phương trình sau: \(\dfrac{x-1}{2023}+\dfrac{x-2}{2022}=\dfrac{x-3}{2021}+\dfrac{x-4}{2020}\)
\(\dfrac{x-1}{2023}+\dfrac{x-2}{2022}=\dfrac{x-3}{2021}+\dfrac{x-4}{2020}\)
`<=>(x-1)/2023-1+(x-2)/2022-1=(x-3)/2021-1+(x-4)/2020-1`
`<=>(x-2024)/2023+(x-2024)/2022=(x-2024)/2021+(x-2024)/2020`
`<=>(x-2024)(1/2023+1/2022-1/2021-1/2020)=0`
`<=>x-2024=0(1/2023+1/2022-1/2021-1/2020>0)`
`<=>x=2024`
Đúng 5
Bình luận (0)
=>\(\left(\dfrac{x-1}{2023}-1\right)+\left(\dfrac{x-2}{2022}-1\right)=\left(\dfrac{x-3}{2021}-1\right)+\left(\dfrac{x-4}{2020}-1\right)\)
=>x-2024=0
=>x=2024
Đúng 3
Bình luận (0)
\(\dfrac{x-1}{2023}+\dfrac{x-2}{2022}=\dfrac{x-3}{2021}+\dfrac{x-4}{2020}\)
⇔\(\dfrac{x-1}{2023}-1+\dfrac{x-2}{2022}-1=\dfrac{x-3}{2021}-1+\dfrac{x-4}{2020}\)
⇔\(\dfrac{x-1}{2023}-\dfrac{2023}{2023}+\dfrac{x-2}{2022}-\dfrac{2022}{2022}=\dfrac{x-3}{2021}-\dfrac{2021}{2021}+\dfrac{x-4}{2020}-\dfrac{2020}{2020}\)
⇔\(\dfrac{x-2024}{2023}+\dfrac{x-2024}{2022}=\dfrac{x-2024}{2021}+\dfrac{x-2024}{2020}\)
⇔\(\dfrac{x-2024}{2023}+\dfrac{x-2024}{2022}-\dfrac{x-2024}{2021}-\dfrac{x-2024}{2020}=0\)
⇔\(\left(x-2024\right)\left(\dfrac{1}{2023}+\dfrac{1}{2022}-\dfrac{1}{2021}-\dfrac{1}{2020}\ne0\right)\)
⇔\(x-2024=0\)
⇔\(x=2024\)
Đúng 1
Bình luận (0)
So sánh: \(\dfrac{2022}{\sqrt{2023}}\) + \(\dfrac{2023}{\sqrt{2022}}\) và \(\sqrt{2022}\) + \(\sqrt{2023}\)
Lời giải:
Xét hiệu:
$\frac{2022}{\sqrt{2023}}+\frac{2023}{\sqrt{2022}}-(\sqrt{2022}+\sqrt{2023})$
$=(\frac{2022}{\sqrt{2023}}-\sqrt{2023})+(\frac{2023}{\sqrt{2022}}-\sqrt{2022})$
$=\frac{2022-2023}{\sqrt{2023}}+\frac{2023-2022}{\sqrt{2022}}$
$=\frac{1}{\sqrt{2022}}-\frac{1}{\sqrt{2023}}>0$
$\Rightarrow \frac{2022}{\sqrt{2023}}+\frac{2023}{\sqrt{2022}}>\sqrt{2022}+\sqrt{2023}$
Đúng 1
Bình luận (0)
Giải phương trình: x²+2013√2(x²+2)=2023√x²-3x+2 -3x-2
Câu 1: Biểu thức sqrt{x^2+2023}-2024 có giá trị nhỏ nhất bằng:A. sqrt{2023}-2021B. -2024C. 0D. sqrt{2023} Câu 2: Chọn khẳng định đúng trong các khẳng định sau:A. Hai góc kề nhau có tổng số đo bằng 1800.B. Hai góc so le trong bằng nhau.C. Hai góc đồng vị bằng nhau.D. Hai góc đối đỉnh bằng nhau. Câu 3: Cho a, b, c là ba đường thẳng phân biệt. Biết a song song với b và b vuông góc với c thì kết luận nào sau đây đúng?A. a song song với c.B. a trùng với c.C. a vuông góc với c.D. a không vuông góc với...
Đọc tiếp
Câu 1: Biểu thức \(\sqrt{x^2+2023}-2024\) có giá trị nhỏ nhất bằng:
A. \(\sqrt{2023}-2021\)
B. -2024
C. 0
D. \(\sqrt{2023}\)
Câu 2: Chọn khẳng định đúng trong các khẳng định sau:
A. Hai góc kề nhau có tổng số đo bằng 1800.
B. Hai góc so le trong bằng nhau.
C. Hai góc đồng vị bằng nhau.
D. Hai góc đối đỉnh bằng nhau.
Câu 3: Cho a, b, c là ba đường thẳng phân biệt. Biết a song song với b và b vuông góc với c thì kết luận nào sau đây đúng?
A. a song song với c.
B. a trùng với c.
C. a vuông góc với c.
D. a không vuông góc với c.
Câu 4: Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiền đề Euclid?
A. Qua điểm A nằm ngoài đường thẳng d có ít nhất một đường thẳng song song với d.
B. Nếu qua điểm A nằm ngoài đường thẳng d mà có hai đường thẳng cùng song song với d thì chúng trùng nhau.
C. Có duy nhất một đường thẳng song song với một đường thẳng cho trước.
D. Cho điểm A nằm ngoài đường thẳng d. Đường thẳng đi qua A và song song với d không phải là đường thẳng duy nhất.
1: Không cớ câu nào đúng
2D
3C
4B
Đúng 0
Bình luận (0)