Gọi độ dài 3 cạnh của tam giác thứ tự là a,b,c (a > 0; b > 0; c > 0).

Vì độ dài 3 cạnh tỉ lệ với 3, 4, 9 nên:

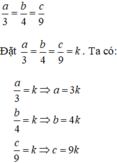
Suy ra: a + b = 3k + 4k = 7k < 9k (hay a + b < c)

Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại)

Vậy không có tam giác nào có 3 cạnh tỉ lệ 3;4;9.

Gọi độ dài 3 cạnh của tam giác thứ tự là a, b, c.

Theo đề bài ta có:

Đặt các tỉ số trên là k. Ta có:

Suy ra: a + b = 3k + 4k = 7k < 9k

Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại).

Vậy không có tam giác nào có 3 cạnh tỉ lệ với 3; 4; 9.

#include <bits/stdc++.h>

using namespace std;

double a,b,c;

bool kt;

int main()

{

cin>>a>>b>>c;

kt=false;

if (a>0 && b>0 && c>0)

{

if (a*a==b*b+c*c) kt=true;

if (b*b==a*a+c*c) kt=true;

if (c*c==a*a+b*b) kt=true;

if (kt==true) cout<<"YES";

else cout<<"NO";

}

else cout<<"NO";

return 0;

}

Var a,b,c:real;

Begin

Write('Nhap a = ');readln(a);

Write('Nhap b = ');readln(b);

Write('Nhap c = ');readln(c);

If (a + b > c) and (b + c > a) and (c + a > b) then

Begin

If (a*a = b*b + c*c) or (b*b = a*a + c*c) or (c*c = a*a + b*b) then

Write('tam giac vuong')

Else write('Khong la tam giac vuong');

End

Else write('ba canh vua nhap khong lap thanh tam giac');

Readln

End.

a) gọi 3 cạnh của tam giác lần lượt là a;b;c ta có

 \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a+b+c =60 

 áp dụng tích chất của dãy tỉ số bằng nhau ta có

  \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)

\(\frac{a}{3}=5=>a=15\)

\(\frac{b}{4}=5=>b=20\)

\(\frac{c}{5}=5=>c=25\)

a, Gọi 3 cạnh của tam giác lần lượt là x, y, t

Ta có: \(\frac{x}{3}=\frac{y}{4}=\frac{t}{5}\)và \(x+y+t=60\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{x}{3}=\frac{y}{4}=\frac{t}{5}=\frac{x+y+t}{3+4+5}=\frac{60}{2}=5\)

\(\frac{x}{3}=5\Rightarrow a=15\)

\(\frac{y}{4}=5\Rightarrow a=20\)

\(\frac{t}{5}=5\Rightarrow a=25\)

Không tồn tại tam giác trên vì: 

\(\sqrt{17}+\sqrt{5+1}\approx6,6< 3\sqrt{5}\)

\(\sqrt{17}+3\sqrt{5}\approx10,83>\sqrt{5+1}\)

\(\sqrt{5+1}+3\sqrt{5}\approx9,16>\sqrt{17}\)

Gọi độ dài ba cạnh lần lượtlà a,b,c

Theo đề, ta co: a/2=b/3=c/4

Áp dụng tính chất của DTSBN, ta được;

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{54}{9}=6\)

=>a=12; b=18; c=24

Gọi \(a,b,c\) lần lượt là độ dài 3 cạnh của 1 tam giác 

Theo bài ra ta có : 

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\) và \(a+b+c=54\)

Áp dụng tính chất của dãy tỉ số bằng nhau : 

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{54}{9}=6\)

\(\Rightarrow\left\{{}\begin{matrix}a=6\times2=12\\b=6\times3=18\\c=6\times4=24\end{matrix}\right.\)

Vậy \(12,18,24\) lần lượt là độ dài 3 cạnh của 1 tam giác .

chuẩn luôn

#include <bits/stdc++.h>

using namespace std;

int main()

{

long long a,b,c,kt;

cin>>a>>b>>c;

kt=0;

if ((a+b>c) and (a+c>b) and (b+c>a))

{

if (a*a==b*b+c*c) kt=1;

if (b*b==a*a+c*c) kt=1;

if (c*c==a*a+b*b) kt=1;

}

if (kt==0) cout<<"wrong"

else cout<<"right";

return 0;

}

dung roi rat la ...

Ta có: \(\hept{\begin{cases}\sqrt{5+1}< \sqrt{16}\\\sqrt{16}< \sqrt{17}\\\sqrt{17}< \sqrt{45}=3\sqrt{5}\end{cases}}\)

Từ đây,ta có: \(\sqrt{5+1}< \sqrt{17}< \sqrt{5}\)

Theo BĐT tam giác thi tổng dài hai cạnh của tam giác luôn lớn hơn cạnh còn lại.

Ta có: \(\sqrt{5+1}+\sqrt{17}=\sqrt{7}+\sqrt{6}\)

Mặt khác,hiển nhiên ta có: với a,b > 0 thì \(a+b< ab\)

Áp dụng vào,ta có: \(\sqrt{5+1}+\sqrt{17}=\sqrt{7}+\sqrt{6}< \sqrt{7}.\sqrt{6}=\sqrt{42}< \sqrt{45}=3\sqrt{5}\)

Từ đây ta có: \(\sqrt{5+1}+\sqrt{17}< 3\sqrt{5}\) (không thỏa mãn)

Vậy không tồn tại tam giác với độ dài 3 cạnh đã cho