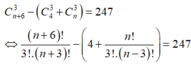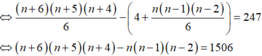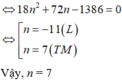Hoàn thiện các câu sau.
Hình tam giác ABC có:
3 đỉnh là: .?., .?., .?.
3 cạnh là:.?.,.?.,.?.
Những câu hỏi liên quan
Cho tam giác đều ABC cạnh a. Tam giác
A
1
B
1
C
1
có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác
A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác
A
1
B
1
C...
Đọc tiếp
Cho tam giác đều ABC cạnh a. Tam giác A 1 B 1 C 1 có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A 2 B 2 C 2 có các đỉnh là trung điểm các cạnh của tam giác A 1 B 1 C 1 , …, tam giác A n + 1 B n + 1 C n + 1 có các đỉnh là trung điểm các cạnh của tam giác A n B n C n , …. Gọi S 1 , S 2 ,..., S n ,... theo thứ tự là diện tích các tam giác A 1 B 1 C 1 , A 2 B 2 C 2 , …, A n B n C n , … . Tìm tổng S = S 1 + S 2 + ... + S n + ...
A. S = a 2 3 3
B. S = a 2 3 8
C. S = a 2 3 12
D. S = a 2 3 16
Đáp án C
Dựa vào dữ kiện đề bài ta có thể suy ra tổng S là tổng của cấp số nhân lùi vô hạn với công bội
q = 1 4 ⇒ S = S 1 1 − q = a 3 3 4 . 1 4 1 − 1 4 = a 2 3 12
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh a. Tam giác
A
1
B
1
C
1
có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác
A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác
A
1
B
1
C...
Đọc tiếp
Cho tam giác đều ABC cạnh a. Tam giác A 1 B 1 C 1 có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A 2 B 2 C 2 có các đỉnh là trung điểm các cạnh của tam giác A 1 B 1 C 1 , …, tam giác A n + 1 B n + 1 C n + 1 có các đỉnh là trung điểm các cạnh của tam giác A n B n C n , …. Gọi S 1 , S 2 , ... , S n , ... theo thứ tự là diện tích các tam giác A 1 B 1 C 1 , A 2 B 2 C 2 , …, A n B n C n , … . Tìm tổng S = S 1 + S 2 + ... + S n + ...
A. S = a 2 3 3
B. S = a 2 3 8
C. S = a 2 3 12
D. S = a 2 3 16
Đáp án C
Dựa vào dữ kiện đề bài ta có thể suy ra tổng S là tổng của cấp số nhân lùi vô hạn với công bội q = 1 4 ⇒ S = S 1 1 − q = a 3 3 4 . 1 4 1 − 1 4 = a 2 3 12
Đúng 0
Bình luận (0)
Cho một tam giác đều ABC cạnh a. Tam giác {A_1}{B_1}{C_1} có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác {A_2}{B_2}{C_2} có các đỉnh là trung điểm các cạnh của tam giác {A_1}{B_1}{C_1}, ldots , tam giác {A_{n + 1}}{B_{n + 1}}{C_{n + 1}} có các đỉnh là trung điểm các cạnh của tam giác {A_n}{B_n}{C_n}, ldots Gọi {p_1},{p_2}, ldots ,{p_n}, ldots và {S_1},{S_2}, ldots ,{S_n}, ldots theo thứ tự là chu vi và diện tích của các tam giác {A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, ldots ,{A_n}{B_n...
Đọc tiếp
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
Tham khảo:
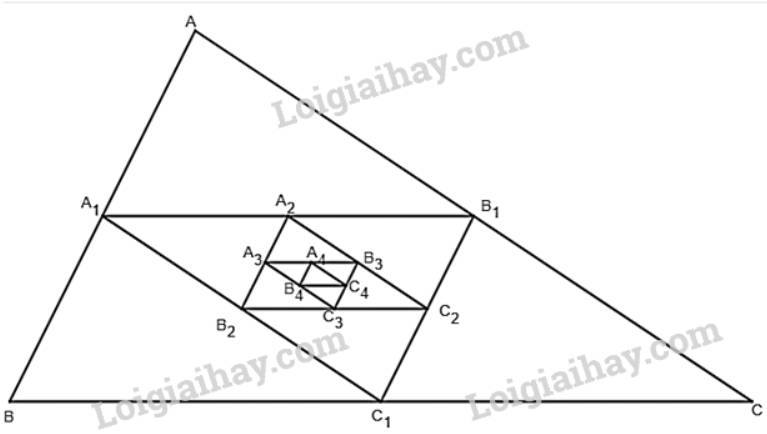
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
Đúng 0
Bình luận (0)
Cho đa giác (H) có n đỉnh
(
n
∈
ℕ
,
n
4
)
. Biết số các tam giác có 3 đỉnh là đỉnh của (H) và không có cạnh nào là cạnh của (H) gấp 5 lần số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 1 cạnh là cạnh của (H). Khẳng định nào sau đây đúng? A.
n
∈...
Đọc tiếp
Cho đa giác (H) có n đỉnh ( n ∈ ℕ , n > 4 ) . Biết số các tam giác có 3 đỉnh là đỉnh của (H) và không có cạnh nào là cạnh của (H) gấp 5 lần số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 1 cạnh là cạnh của (H). Khẳng định nào sau đây đúng?
A. n ∈ 4 ; 12
B. n ∈ 13 ; 21
C. n ∈ 22 ; 30
D. n ∈ 31 ; 38
Chọn D
Lời giải. Số tam giác tạo thành có 3 đỉnh là 3 đỉnh của đa giác là C n 3
Số tam giác tạo thành có đúng 2 cạnh là cạnh của đa giác là n
Số tam giác tạo thành có đúng 1 cạnh là cạnh của đa giác là n(n-4)
(điều kiện n ∈ ℕ v à n < 4 )
→ số tam giác tạo thành không có cạnh nào là cạnh của đa giác là
Theo giả thiết, ta có
⇔ n = 35 ( t h ỏ a m ã n ) n = 4 ( l o ạ i )
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh 8cm. Chia tam giac này thành 64 tam giác nhỏ đều cạnh 1cm bởi các đường thẳng song song với các cạnh tam giác ABC.S là tập hợp các đỉnh tam giác cạnh 1cm. Chọn ngẫu nhiên 4 đỉnh thuộc S. Tính XÁC SUẤT sao cho 4 đỉnh được chọn là 4 đỉnh của hình bình hành miền trong tam giác ABC và có cạnh chứa các cạnh của tam giác có cạnh 1cm ở trên.
chắc như mọi người nói
Cho tam giác đều ABC như hình 01. Em hãy trả lời các câu hỏi sau:
a) Liệt kê các đỉnh, các cạnh của tam giác ABC.
b) Em có nhận xét gì về độ dài 3 cạnh của tam giác ABC.
A B C Hình 01
Đọc tiếp
Cho tam giác đều ABC như hình 01. Em hãy trả lời các câu hỏi sau:
a) Liệt kê các đỉnh, các cạnh của tam giác ABC.
b) Em có nhận xét gì về độ dài 3 cạnh của tam giác ABC.
Cho đa giác lồi 14 đỉnh. Gọi X là tập hợp các tam giác có 3 đỉnh là 3 đỉnh của đa giác đã cho. Chọn ngẫu nhiên trong X một tam giác. Tính xác suất để tam giác được chọn không có cạnh nào là cạnh của đa giác đã cho.
A
.
15
26
B
.
1
11
C
.
10
11
D
.
7...
Đọc tiếp
Cho đa giác lồi 14 đỉnh. Gọi X là tập hợp các tam giác có 3 đỉnh là 3 đỉnh của đa giác đã cho. Chọn ngẫu nhiên trong X một tam giác. Tính xác suất để tam giác được chọn không có cạnh nào là cạnh của đa giác đã cho.
A . 15 26
B . 1 11
C . 10 11
D . 7 13
Vẽ hình để thấy được mỗi câu sau đây là saia) Hình gồm 3 đoạn thẳng được gọi là tam giácb) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.f) Một điểm không thuộc cạnh của tam giác ABC thì phải là đỉnh của tam giác đó.g) Một điểm không phải là đỉnh của tam giác AB...
Đọc tiếp
Vẽ hình để thấy được mỗi câu sau đây là sai
a) Hình gồm 3 đoạn thẳng được gọi là tam giác
b) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.
c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.
d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.
e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.
f) Một điểm không thuộc cạnh của tam giác ABC thì phải là đỉnh của tam giác đó.
g) Một điểm không phải là đỉnh của tam giác ABC thì phải nằm trong tam giác đó.
h) Một điểm không nằm bên trong tam giác ABC thì phải nằm ngoài tam giác đó.
i) Hình gồm 2 góc được gọi là tam giác.
j) Hình gồm 3 góc mà các cạnh của nó đôi một cắt nhau tạo ra ba điểm được dọi là tam giác.
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
Đọc tiếp
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247 A. 6. B. 8 C. 7. D. 5
Đọc tiếp
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247
A. 6.
B. 8
C. 7.
D. 5
Đáp án C
Nhận xét: Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng, tức là không cùng nằm trên một cạnh của tam giác ABC.
Chọn ngẫu nhiên 3 điểm từ n + 6 điểm đã cho có: C n + 6 3 (cách)
Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của tam giác ABC có: C 4 3 + C n 3 (cách)
Số tam giác lập thành là:
Đúng 0
Bình luận (0)