Chọn mốc thế năng ở vị trí cân bằng

a. Ta có cơ năng

W = m g z = m g l ( 1 − cos 60 0 ) = 0 , 5.10.1 ( 1 − 0 , 5 ) = 2 , 5 ( J )

b. Theo định luật bảo toàn cơ năng

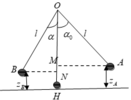
W A = W B ⇒ m g z A = 1 2 m v B 2 + m g z B ⇒ v B = 2 g ( z A − z B ) ( 1 ) M à   z A = H M = l − O M = l − l cos α 0 z B = l − l cos α  

Thay vào ( 1 ) ta có 

v B = 2 g l ( cos α − cos α 0 ) +   K h i   α = 30 0   ⇒ v B = 2 g l ( cos 30 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 3 2 − 1 2 ) ≈ 2 , 71 ( m / s )

+   K h i   α = 45 0   ⇒ v B = 2 g l ( cos 45 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 2 2 − 1 2 ) ≈ 2 , 035 ( m / s )

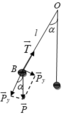
Xét tai B theo định luật II Newton ta có:  P → + T → = m a →

Chiếu theo phương của dây

T − P y = m a h t ⇒ T − P cos α = m v 2 l ⇒ T − m g cos α = 2 m g ( cos α − cos α 0 ) ⇒ T = m g ( 3 cos α − 2 cos α 0 )

Khi  α = 30 0 ⇒ T = m g ( 3 cos 30 0 − 2 cos 60 0 )

⇒ T = 0 , 5.10 ( 3. 3 2 − 2. 1 2 ) = 7 , 99 ( N )

Khi  α = 45 0   ⇒ T = m g ( 3 cos 45 0 − 2 cos 60 0 )

⇒ T = 0 , 5.10 ( 3. 2 2 − 2. 1 2 ) = 5 , 61   N

Lưu ý: Khi làm trắc nghiệm thì các em áp dụng luôn hai công thức

+ Vận tốc của vật tại vị trí bất kỳ:  v B = 2 g l ( cos α − cos α 0 )

+ Lực căng của sợi dây:  T = m g ( 3 cos α − 2 cos α 0 )

c. Gọi C là vị trí để vật có  v= 1,8m/s

Áp dụng công thức  v C = 2 g l ( cos α − cos α 0 )

1 , 8 = 2.10.1 ( cos α − cos 60 0 ) ⇒ cos α = 0 , 662 ⇒ α = 48 , 55 0

Vật có đọ cao

  z C = l − l cos α = 1 − 1.0 , 662 = 0 , 338 ( m )

d. Gọi D là vị trí vật có độ cao 0,18m

Áp dụng công thức 

z D = l − l cos α ⇒ 0 , 18 = 1 − 1. cos α ⇒ cos α = 0 , 82

Áp dụng công thức 

v D = 2 g l ( cos α − cos α 0 ) = 2.10.1. ( 0 , 82 − 0 , 5 ) = 2 , 53 ( m / s )

e. Gọi E là vị trí mà 2 w t = w đ  Theo định luật bảo toàn cơ năng  W A = W E

   W A = W d E + W t E = 3 2 W d E ⇒ 2 , 5 = 3 2 . 1 2 . m v E 2 ⇒ v E = 2 , 5.4 3. m = 10 3.0 , 5 = 2 , 581 ( m / s )  

f.  Gọi F là vị trí để 2  w t = 3 w đ

Theo định luật bảo toàn cơ năng   W A = W F

W A = W d F + W t F = 5 3 W t F ⇒ 2 , 5 = 5 3 . m g z F ⇒ z F = 2 , 5.3 5. m . g = 0 , 3 ( m ) M à   z F = l − l cos α F ⇒ 0 , 3 = 1 − 1. cos α F ⇒ cos α F = 0 , 7 ⇒ α F = 45 , 573 0

Mặt khác  v F = 2 g l ( cos α F − cos 60 0 ) = 2.10.1 ( 0 , 7 − 0 , 5 ) = 2 ( m / s )

Xét tại F theo định luật II Newton   P → + T → = m a →

Chiếu theo phương của dây 

− P cos α F + T F = m v F 2 l ⇒ − 0 , 5.10.0 , 7 + T F = 0 , 5. 2 2 1 ⇒ T = 5 , 5 ( N )

Câu hỏi của Chivas Nguyễn - Vật lý lớp 12 | Học trực tuyến

v m a x = ω S 0  = 0,21.2,9 = 0,609 = 0,61m/s

a = 0 m/ s 2

1/2.m v 2 m a x  = mgl(1 - cos α 0 )

F - mg = m v 2 m a x /l ⇒ F = m(g +  v 2 m a x /l)

F = 0,05(9,8 + 2 , 3 2 /2) ≈ 0,62N

Đáp án D

Ta có:

v max = 2 g l ( 1 - cos   α   max ) = 10 ≈ 3 , 16 ( m / s )