Cho △ABC cân tại A ( góc A<90°). Kẻ AH ⊥ BC tại H. a) △AHB =△AHC. Từ đó => BAH = CAH. b) trên tia AH lấy điểm K sao cho H là trung điểm AK

Những câu hỏi liên quan
Câu 1) cho tam giác ABC cân tại A (ABAC) . Gọi D, E lần lượt là trung điểm của AB và ACa) CM tam giác ABEtam giác ACDb)CM BECDc) Gọi K là trung điểm của BE và CD. Chứng minh tam giác KBC cân tại Kd) CM AK là tia phân giác của góc BACCâu 2) cho tam giác ABC cân tại A. Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm Q và R sao cho BQCRa) CM. AQARb) gọi H là trung điểm của BC. CM góc QAHgóc RAHCâu3)cho tam giác ABC có ABAC5cm ; BC 8cm. Kẻ AH vuông góc BC ( H thuộc BC)a) CM HBHC và góc BAH...
Đọc tiếp
Câu 1) cho tam giác ABC cân tại A (AB=AC) . Gọi D, E lần lượt là trung điểm của AB và AC
a) CM tam giác ABE=tam giác ACD
b)CM BE=CD
c) Gọi K là trung điểm của BE và CD. Chứng minh tam giác KBC cân tại K
d) CM AK là tia phân giác của góc BAC
Câu 2) cho tam giác ABC cân tại A. Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm Q và R sao cho BQ=CR
a) CM. AQ=AR
b) gọi H là trung điểm của BC. CM góc QAH=góc RAH
Câu3)cho tam giác ABC có AB=AC=5cm ; BC= 8cm. Kẻ AH vuông góc BC ( H thuộc BC)
a) CM HB=HC và góc BAH=góc CAH
b) tính độ dài AH
c) kẻ AH vuông góc AB (D thuộcAB) HE vuông góc AC( E thuộc AC) CMR tam giác HDE cân
Từng bài 1 thôi nha!
Mình làm bài 3 cho dễ
Bn tự vẽ hình
a) CM tg ABH=tg ACH (ch-cgv)
=> HC=HB=2 góc tương ứng
Nên H là trung điểm BC
=> HB=HC=BC:2=8:2=4 ; góc BAH= góc CAH
b) Có: tg ABH vuông tại H (AH vuông góc BC)
=> AH2+BH2=AB2 => AH2+42=52 => AH2=9
Mà AH>O Nên AH=3
c) Xét tg ADH và tg AEH có:
\(\Delta ADH=\Delta AEH\left(ch-gh\right)\hept{\begin{cases}\widehat{ADH}=\widehat{AEH}=90^o\\AHcanhchung\\\widehat{DAH}=\widehat{EAH}\left(\Delta ABH=\Delta ACH\right)\end{cases}}\)
=> HD=HE(2 góc tương ứng)
=> tg HDE cân tại H
Đúng 0
Bình luận (0)
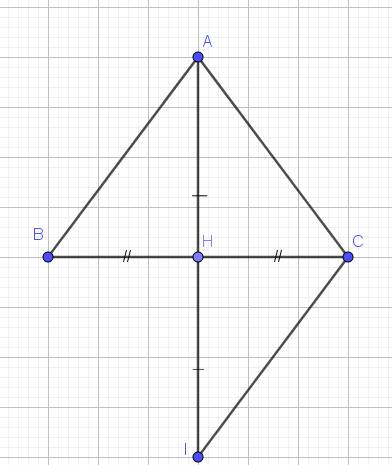
Cho △ABC cân tại A , ( góc A < 90 độ ) . Gọi H tại trung điểm BC , Chứng minh :
a, △ABH = △ACH
b, AH là đường trung trực của BC
c, Trên tia đối của HA lấy điểm I sao cho HA = HI . Chứng minh : IC // AB và ∠CAH = ∠CIH
Lời giải:
a. Xét tam giác $ABH$ và $ACH$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$AH$ chung
$BH=CH$ (do $H$ là trung điểm $BC$)
$\Rightarrow \triangle ABH=\triangle ACH$ (c.c.c)
b. Từ tam giác bằng nhau phần a suy ra $\widehat{AHB}=\widehat{AHC}$
Mà $\widehat{AHB}+\widehat{AHC}=\widehat{BHC}=180^0$
$\Rightarrow \widehat{AHB}=\widehat{AHC}=90^0$
$\Rightarrow AH\perp BC$
Vậy $AH\perp BC$ tại trung điểm $H$ của $BC$ nên $AH$ là trung trực $BC$
c. Xét tam giác $ABH$ và $ICH$ có:
$\widehat{AHB}=\widehat{IHC}$ (đối đỉnh)
$AH=IH$
$BH=CH$
$\Rightarrow \triangle ABH=\triangle ICH$ (c.g.c)
$\Rightarrow \widehat{ABH}=\widehat{ICH}$
Mà 2 góc này ở vị trí so le trong nên $IC\parallel AB$
Từ tam giác bằng nhau ở trên suy ra $\widehat{CIH}=\widehat{BAH}(1)$
Từ tam giác bằng nhau phần a suy ra $\widehat{BAH}=\widehat{CAH}(2)$
Từ $(1); (2)\Rightarrow \widehat{CIH}=\widehat{CAH}$
Đúng 1
Bình luận (0)
B1 cho tam giác ABC có góc A 90 độ , AH vuông góc với BC tại H. Vẽ các điểm I, K sao cho AB là trung trực HI và AC là trung trực HK a) CMinh : AIAKb) CM: 3 điểm I, A,K thẳng hàngc) Cho góc CAH 30 độ . Tính góc ABC B2 cho tam giác ABC có góc A 90 độ, Ah vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D ko cùng nửa mặt phảng ờ BC với điểm A sao cho AHBDa) CMinh: tam giác AHB tam giác DHBb) AB và DH có song song ko ?c) tính góc ACB biết góc BAH 35 độ
Đọc tiếp
B1 cho tam giác ABC có góc A = 90 độ , AH vuông góc với BC tại H. Vẽ các điểm I, K sao cho AB là trung trực HI và AC là trung trực HK
a) CMinh : AI=AK
b) CM: 3 điểm I, A,K thẳng hàng
c) Cho góc CAH = 30 độ . Tính góc ABC
B2 cho tam giác ABC có góc A = 90 độ, Ah vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D ko cùng nửa mặt phảng ờ BC với điểm A sao cho AH=BD
a) CMinh: tam giác AHB= tam giác DHB
b) AB và DH có song song ko ?
c) tính góc ACB biết góc BAH= 35 độ
1. Cho ∆ABC có AB < AC. Vẽ AH vuông góc BC (H∈BC); HI vuông góc AC tại I. Trên tia đối của tia IH lấy điểm E sao cho IE = HI. Chứng minh:
a/ AE vuông góc CE. b/ góc BAH < góc CAH.
2. Cho ∆ABC vuông tại A. Trên cạnh AC lấy các điểm D và E sao cho AD = DE = EC. So sánh góc ABD và góc DBE.
--> Giúp e làm hai bài trên đi aaa :33 <3
Cho tam giác ABC cân tại A ( góc A< 90 độ ) Gọi H là trung điểm BC a) Cm tam giác ABH = tam giác ACH b) Cm aH là đường trung trực của BC c) Trên tia đối của tia HA lấy điểm I sao cho HA = HI. Cm IC// AB và góc CAH= góc CIH vẽ hình giúp e với ạ
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔABC cân tại A
mà AH là đường cao
nên AH là trung trực của BC
c: Xét tứ giác ABIC có
H là trung điểm chung của AI và BC
AI vuông góc bC
=>ABIC là hình thoi
=>IC//AB và IC=AB
=>CA=CI
=>góc CAH=góc CIH
Đúng 2
Bình luận (1)
Cho tam giác ABC (AB < AC), vẽ đường cao AH
a. Chứng minh góc BAH < góc CAH và BH < CH
b. Trên tia đối của HA lấy điển E sao cho HE = HA.
Chứng minh ABE cân.
c. Gọi M là trung điểm của BC trên tia đối của MA lấy
điểm D sao cho MD = MA. Chứng minh AED vuong
Cho tam giác ABC vuong tại A, vẽ AH vuông góc với BC cắt BC tại H.
a) Chứng minh: Góc BAH bằng góc C.
b) Chứng minh: Góc CAH bằng góc B.
c) Trên tia AH lấy I sao cho H là trung điểm AI, qua I vẽ tia song song với AB cắt BC D. Chứng minh: DI = AB
d) Chứng minh: AD = DI
Cho tam giác ABC vuông tại A. Kẻ AH vuông BC tại H. Kẻ tia phân giác AD của góc BAH (D∈BC)a) Chứng minh: ^BAH^C, ^CAH^Bb) Chứng minh: ΔACDcânc) Kẻ DK vuông BC, cắt AB tại K. Chứng minh ΔKAD când) CK là tia phân giác của ^C và CK là đường trung trực ABe) Trên cạnh AB lấy điểm I sao cho AI AH. Chứng minh DI // AC
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ AH vuông BC tại H. Kẻ tia phân giác AD của góc BAH (D∈BC)
a) Chứng minh: ^BAH=^C, ^CAH=^B
b) Chứng minh: ΔACDcân
c) Kẻ DK vuông BC, cắt AB tại K. Chứng minh ΔKAD cân
d) CK là tia phân giác của ^C và CK là đường trung trực AB
e) Trên cạnh AB lấy điểm I sao cho AI = AH. Chứng minh DI // AC
Cho 🔺 ABC vuông tại A (AB<AC). Trên tia đối của tia AB, lấy điểm E sao cho AE=AC. Trên tia đối của tia AC, lấy điểm D sao cho AD=AB
a) Chứng minh 🔺ABC=🔺ADE
b) Vẽ AH vuônh góc với BC tại H. Chứng minh góc BAH = góc ACH
c) Tia HA cắt DC tại K. Chứng minh K là trung điểm của DE
d) Chứng minh BC // CE