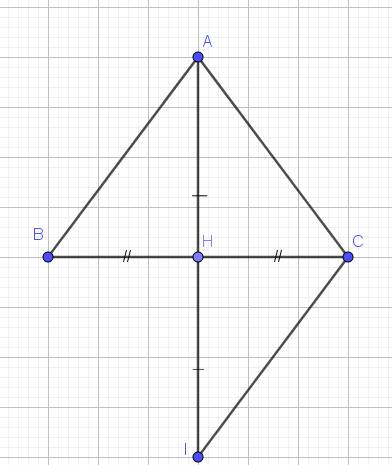
Lời giải:
a. Xét tam giác $ABH$ và $ACH$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$AH$ chung
$BH=CH$ (do $H$ là trung điểm $BC$)
$\Rightarrow \triangle ABH=\triangle ACH$ (c.c.c)
b. Từ tam giác bằng nhau phần a suy ra $\widehat{AHB}=\widehat{AHC}$
Mà $\widehat{AHB}+\widehat{AHC}=\widehat{BHC}=180^0$
$\Rightarrow \widehat{AHB}=\widehat{AHC}=90^0$
$\Rightarrow AH\perp BC$
Vậy $AH\perp BC$ tại trung điểm $H$ của $BC$ nên $AH$ là trung trực $BC$
c. Xét tam giác $ABH$ và $ICH$ có:
$\widehat{AHB}=\widehat{IHC}$ (đối đỉnh)
$AH=IH$
$BH=CH$
$\Rightarrow \triangle ABH=\triangle ICH$ (c.g.c)
$\Rightarrow \widehat{ABH}=\widehat{ICH}$
Mà 2 góc này ở vị trí so le trong nên $IC\parallel AB$
Từ tam giác bằng nhau ở trên suy ra $\widehat{CIH}=\widehat{BAH}(1)$
Từ tam giác bằng nhau phần a suy ra $\widehat{BAH}=\widehat{CAH}(2)$
Từ $(1); (2)\Rightarrow \widehat{CIH}=\widehat{CAH}$