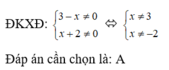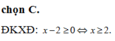\(x-\sqrt{1-x}=\sqrt{x-2}+3\)

\(ĐK:\left\{{}\begin{matrix}1-x\ge0\\x-2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\x\ge2\end{matrix}\right.\Leftrightarrow x\in\varnothing\)

Vậy PT vô nghiệm

ĐKXĐ: \(x-2\ne0\)

\(\Leftrightarrow x\ne2\)

trả lời câu hỏi này cho mình nhé mình cảm ơn

ĐKXĐ : x ≠ ±2

giải pt thì chịu còn điều kiện thì biết

x^2-x+1>0

x^2-x-2>0

Lời giải:

$mA=\sqrt{x}-2$

$\Leftrightarrow \frac{m(2\sqrt{x}-1)}{\sqrt{x}+1}=\sqrt{x}-2$
$\Rightarrow m(2\sqrt{x}-1)=(\sqrt{x}+1)(\sqrt{x}-2)$

$\Leftrightarrow 2m\sqrt{x}-m=x-\sqrt{x}-2$
$\Leftrightarrow x-\sqrt{x}(2m+1)+(m-2)=0(*)$
Để pt ban đầu có 2 nghiệm pb thì $(*)$ phải có 2 nghiệm dương phân biệt.

Điều này xảy ra khi mà:
\(\left\{\begin{matrix}\ \Delta=(2m+1)^2-4(m-2)>0\\ S=2m+1>0\\ P=m-2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4m^2+9>0\\ m> \frac{-1}{2}\\ m>2\end{matrix}\right.\Leftrightarrow m>2\)

a, ĐKXĐ : x ≠ 4

b,

\(\Leftrightarrow3x+2=2\left(x-4\right)\)

\(\Leftrightarrow3x+2=2x-8\)

\(\Leftrightarrow x=-10\) (N)

Vậy : ...

`a)` Ptr xác định `<=>x-4 \ne 0<=>x \ne 4`

`b)[3x+2]/[x-4]=2`         `ĐK: x \ne 4`

`<=>3x+2=2(x-4)`

`<=>3x+2=2x-8`

`<=>3x-2x=-8-2`

`<=>x=-10` (t/m)

Vậy `S={-10}`

Lời giải:
ĐKXĐ: $9x^2+6x+1\geq 0$

$\Leftrightarrow (3x+1)^2\geq 0$

$\Leftrightarrow x\in\mathbb{R}$
--------------------------

$\sqrt{9x^2+6x+1}=2-x$

\(\Rightarrow \left\{\begin{matrix} 2-x\geq 0\\ 9x^2+6x+1=(2-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 9x^2+6x+1=x^2-4x+4\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 8x^2+10x-3=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ (4x-1)(2x+3)=0\end{matrix}\right.\Leftrightarrow x=\frac{1}{4}\) hoặc $x=\frac{-3}{2}$

ĐKXĐ: 

\(x-3\ne0\Rightarrow x\ne3\)