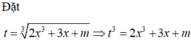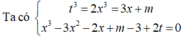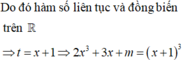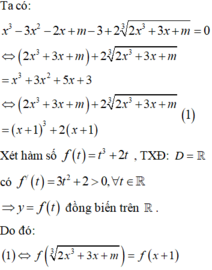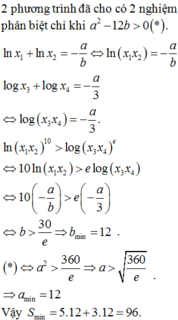Cho a , b , c là các nghiệm của phương trình x3 - 3x + 1 = 0 . Tính S = a9 + b9 + c9 .

Những câu hỏi liên quan
Cho phương trình
x
3
-
3
x
2
-
2
x
+
m
-
3
+
2
2
x
3
+
3
x
+
m
3
0
. Tập S là tập hợp các giá trị của m ng...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 - 2 x + m - 3 + 2 2 x 3 + 3 x + m 3 = 0 . Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân biệt. Tính tổng các phần tử của S.
A. 15.
B. 9.
C. 0.
D. 3.
Đáp án là B
Đặt ![]()
![]()
Ta có
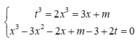
![]()
Xét hàm số
![]()
![]()
Do đó hàm số liên tục và đồng biến trên ℝ
![]()
![]()
Xét ![]()
![]()
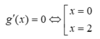
Bảng biến thiên

Từ bảng biến thiên suy ra -5 < -m < -1
![]()
Vậy tổng các phần tử của S bằng 9.
Đúng 0
Bình luận (0)
Cho phương trình
x
3
-
3
x
2
-
2
x
+
m
-
3
+
2
2
x
3
+
3
x
+
m
3
0
. Tập S là tập hợp các giá trị của m nguyên để phương trình...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 - 2 x + m - 3 + 2 2 x 3 + 3 x + m 3 = 0 . Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân biệt. Tính tổng các phần tử của S.
A. 15.
B. 9.
C. 0.
D. 3.
cho a b c là các nghiệm của phương trình x^3-3x+1=0 .Tính S=a^9+b^9+c^9
Cho a,b,c là các nghiệm của phương trình x3-3x+1=0. Tính S= a9+b9+c9
Cho phương trình
x
3
-
3
x
2
-
2
x
+
m
-
3
+
2
2
x
3
+
3
x
+
m
3
. Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 - 2 x + m - 3 + 2 2 x 3 + 3 x + m 3 . Tập S là tập hợp các giá trị của m nguyên để phương trình có ba nghiệm phân biệt. Tính tổng các phần tử của S
A. 15.
B. 9.
C. 0.
D. 3.
Cho phương trình
(
m
-
5
)
.
3
x
+
(
2
m
-
2
)
.
2
x
.
3
x
+
(
1
-
m
)
.
4
x
0
, tập hợp tất cả các giá trị của tham số m để phương trì...
Đọc tiếp
Cho phương trình ( m - 5 ) . 3 x + ( 2 m - 2 ) . 2 x . 3 x + ( 1 - m ) . 4 x = 0 , tập hợp tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt là khoảng (a;b). Tính S=a+b
A.4
B.5
C.6
D.8
Biết phương trình
3
x
+
1
−
3
x
2
+
7
x
−
3
x
−
1
0
có một nghiệm có dạng
x
a
+
b
c
, trong đó a, b, c là các số nguyên tố. T...
Đọc tiếp
Biết phương trình 3 x + 1 − 3 x 2 + 7 x − 3 x − 1 = 0 có một nghiệm có dạng x = a + b c , trong đó a, b, c là các số nguyên tố. Tính S=a+b+c
A. S = 14
B. S = 21
C. S = 10
D. S = 12
Điều kiện: 3 x 2 + 7 x ≥ 0 3 x − 1 ≥ 0 ⇔ x ≥ 1 3 *
Với điều kiện trên, phương trình tương đương
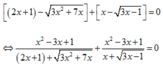
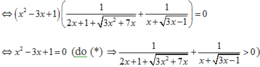
![]()
Theo yêu cầu đề bài ta chọn nghiệm x = 3 + 5 2
Vậy a = 3 , b = 5 , c = 2 ⇒ S = a + b + c = 10
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho hai phương trình x2+2022x+1=0 (1) và x2+2023x+1 (2).Gọi x1,x2 là nghiệm của phương trình (1) ; x3,x4 là nghiệm của phương trình (2).Giá trị của biểu thức P=(x1+x3)(x2+x3)(x1-x4)(x2-x4) là
A.4045 B.-1 C.1 D.0
Xét các số nguyên dương a,b sao cho phương trình
b
ln
2
x
+
a
ln
x
+
3
0
có hai nghiệm phân biệt
x
1
,
x
2
và phương trình
3
log
2
x
+
a
log
x
+
b
0
có hai nghiệ...
Đọc tiếp
Xét các số nguyên dương a,b sao cho phương trình b ln 2 x + a ln x + 3 = 0 có hai nghiệm phân biệt x 1 , x 2 và phương trình 3 log 2 x + a log x + b = 0 có hai nghiệm phân biệt x 3 , x 4 thỏa mãn ln x 1 x 2 10 > log x 3 x 4 6 Tính giá trị nhỏ nhất của S=5a + 3b
A. 102
B. 101
C. 96
D. 99