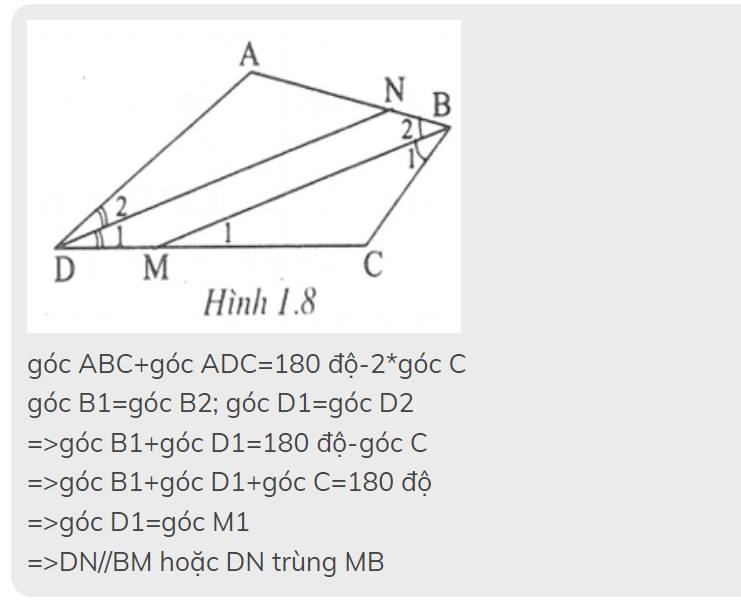
Cho tứ giác ABCD biết góc B=D=90.Vẽ các đường phân giác của A và C. Biết 2 dường thẳng này không trùng nhau.Chứng minh hai đường thẳng song song?

Những câu hỏi liên quan
Cho tứ giác ABCD, góc B = góc D = 90 độ.
Vẽ các đường phân giác của góc A và góc C. Cho biết 2 đường phân giác này không trùng nhau, chứng minh rằng chúng song song với nhau.
ĐANG CẦN GẤP LẮM NHA!!!
Cho tứ giác ABCD có góc B= góc D = 90độ vẽ các đường phân giác của góc A và góc C cho biết 2 đường phân giác này ko trùng nhau .chứng minh rằng chúng song song
1. Tứ giác ABCD, góc B= góc D= 90 độ, vẽ phân giác góc A,C biết 2 đường phân giác này không trùng nhau. Chứng minh chúng song song với nhau
2. Cho tứ giác ABCD, giác định điểm M sao cho: MA+MB+MC+MD có giá trị nhỏ nhất
Cho tứ giác ABCD có B=D=90 độ.Vẽ phân giác góc A và C biết 2 phân giác này không trùng nhau.CM 2 phân giác đó song song với nhau
Lm nhanh mik tick
Gọi AE là phân giác góc A( E thuộc CD), CF là phân giác góc C ( F thuộc AB )
H là giao điểm của DA và CF.
Xét \(\Delta DHC\)và \(\Delta BCF\)có:
\(\widehat{B}=\widehat{D}=90^o\)
\(\widehat{DCH}=\widehat{BCF}\left(gt\right)\)
Suy ra \(\Delta DHC\)đồng dạng với \(\Delta BCF\)(g.g)
\(\Rightarrow\widehat{DHC}=\widehat{BFC}\)
Mà \(\widehat{AFH}=\widehat{BFC}\)(ĐỐI ĐỈNH)
nên \(\widehat{AFH}=\widehat{DHC}\)hay \(\widehat{AFH}=\widehat{AHF}\)
Ta có:
\(\widehat{DAF}\)là góc ngoài của \(\Delta AHF\)
\(\Rightarrow\widehat{DAF}=\widehat{AHF}+\widehat{AFH}\)
\(\Leftrightarrow2.\widehat{AFH}=\widehat{DAF}\)
\(\Leftrightarrow\widehat{AFH}=\widehat{\frac{DAF}{2}=\widehat{BAE}}\)
Mà \(\widehat{AFH}=\widehat{BFC}\)(ĐỐI ĐỈNH) nên \(\widehat{BAE}=\widehat{BFC}\)
\(\Rightarrow AE\)//\(CF\)(Vì có hai góc so le trong bằng nhau)
Vậy AE//CF
Đúng 0
Bình luận (0)
cho tứ giác ABCD có A=C=90 Vẽ tia phân giác của góc B cắt AD tại E .Qua D kẻ đường thẳng song song với BE cắt BC tại F.Chứng minh rằng DF là tia phân giác của góc D
Ta có:
+, Gọi giao của DC và BE là K
Vì DF//BE nên gócCDF =góc CKB ( 2 góc đồng vị )
mà góc CKB +gócCBK =900 ( vì gócC=900 ) ( 1)
+, gócCBK =gócABE ( vì BE là tia pg của gócB)
và gócABE =gócAFD ( vì BE//DF)
=> gócCBK= gócAFD (2)
mà gócAFD +gócADF=900 (vì góc A=900) (3)
Từ (1)(2)(3) ta có góc ADF = góc CDF
=> DF là tia pg của góc D ( đpcm )
Cho mik 1 like nhé!!! Chúc bạn làm bài tốt .
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc A = góc C = 90°. Vẽ tia phân giác của góc B cắt AC tại E. Qua D kẻ đường thẳng song song với BE cắt BC tại F. Chứng minh rằng DF là tia phân giác của góc ADC
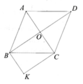
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua và song với AC, vẽ đường thẳng qua C và song song với BD, hai đường chéo này cắt nhau tại K a) Chứng minh rằng tứ giác OBKC là hình chữ nhật b) Chứng minh tứ giác ABKO là hình bình hành c) Tìm điều kiện về hai đường chéo của hình thoi ABCD để tứ giác OBKC kà hình vuông
THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân có góc A = 90 độ. Gọi M là trung điểm của AB. Từ M vẽ đường thẳng song song AC cắt BC tại H. Từ C vẽ đường thẳng song song AB cắt MH tại N
a) Chứng minh tứ giác AMNC là hình chữ nhật
b) Gọi D là giao điểm của hai đường thẳng AH và CN. Chứng minh tứ giác ABDC là hình vuông
Bài 1: Tứ giác ABCD có Â =C. Chứng minh rằng các đường phân giác của góc B và góc D song song với nhau hoặc trùng nhau
Bài 2: Chứng minh rằng trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác.