Xác định một đa thức bậc ba f(x) không có hạng tử tự do sao cho : \(f\left(x\right)-f\left(x-1\right)=x^2\)

Những câu hỏi liên quan
Xác định một đa thức bậc ba f(x) không có hạng tử tự do sao: cho
f(x) - f(x-1)=x2
Xác định đa thức f(x) có bậc ba thỏa mãn: \(f\left(x+1\right)-f\left(x\right)=x^2\left(\forall x\right)\) và \(f\left(2\right)=2020\)
Cho đa thức: \(f\left(x\right)=x+x^2-6x^3+3x^4+2x^2+6x-2x^4+1\)
1. Thu gọn, rồi sắp xếp các số hạng của đa thức theo lũy thừa giảm dần của biến \(x\)
2. Xác định, bậc của đa thức, hệ số tự do, hệ số cao nhất
3. Tính \(f\left(-1\right),f\left(0\right),f\left(1\right),f\left(-a\right)\)
1. \(f\left(x\right)=x+x^2-6x^3+3x^4+2x^2+6x-2x^4+1\)
\(\Rightarrow f\left(x\right)=7x+3x^2-6x^3+x^4+1\)
Sắp xếp theo lũy thừa giảm dần của biến x:
\(f\left(x\right)=x^4-6x^3+3x^2+7x+1\)
2. Bậc của đa thức: 4
Hệ số tự do: 1
Hệ số cao nhất: 7
3. \(f\left(-1\right)=\left(-1\right)^4-6.\left(-1\right)^3+3.\left(-1\right)^2+7.\left(-1\right)+1=4\)
\(f\left(0\right)=0^4-6.0^3+3.0^2+7.0+1=1\)
\(f\left(1\right)=1^4-6.1^3+3.1^2+7.1+1=6\)
\(f\left(-a\right)=\left(-a\right)^4-6.\left(-a\right)^3+3.\left(-a\right)^2+7.\left(-a\right)+1=3a+1\)
\(\)
Cho đa thức:\(f\left(x\right)=4x^2-7x^2+4x-5x^4-x^2+6x^3+5x^4-5\)
a)Thu gọn rồi sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biến .
b)Xác định bậc của đa thức ,hệ số tự do ,hệ số cao nhất.
c)Tính f(-1);f(0);f(0,5);f(1)
Đồ thị của hàm số \(y = f\left( x \right) = - {x^2} + x + 3\)được biểu diễn trong hình 1
a) Biểu thức \(f\left( x \right)\) là đa thức bậc mấy?
b) Xác định dấu của \(f\left( 2 \right)\)
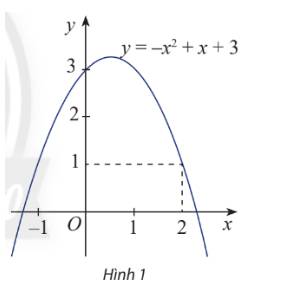
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai
b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:
\(f\left( 2 \right) = - {2^2} + 2 + 3 = 1 > 0\)
Suy ra \(f\left( 2 \right)\) dương.
Đúng 0
Bình luận (0)
cho đa thức f(x) xác định với mọi x thỏa mãn:
\(x\cdot f\left(x+2\right)=\left(x^2-9\right)\cdot f\left(x\right)\)
a) tính giá trị của f(5)
b) CMR ;đa thức f(x) có ít nhất 3 nghiệm
cho đa thức f(x) xác định với mọi x thoả mãn:
\(x\times f\left(x+2\right)=\left(x^2-9\right)\times f\left(x\right)\)
1) tính f(5)
2) chứng minh rằng f(x) có ít nhất 3 nghiệm
1) Thay x=3 vào đẳng thức, thu được:
\(3\times f\left(3+2\right)=\left(3^2-9\right)\times f\left(3\right)\)
\(\Leftrightarrow\) \(3\times f\left(5\right)=0\times f\left(3\right)=0\)
\(\Leftrightarrow\) \(f\left(5\right)=0\)
2) Ta đã chứng minh x=5 là nhiệm của f(x)\(\Rightarrow\)Cần chứng minh f(x) có 2 nghiệm nữa
Thay x=0 Vào đẳng thức, thu được\(0\times f\left(0+2\right)=\left(0^2-9\right)\times f\left(0\right)\)
\(\Leftrightarrow\) \(f\left(0\right)=0\)
\(\Rightarrow\)x=0 là ngiệm của f(x)
Thay x=-3 và đẳng thức, thu được\(-3\times f\left(-3+2\right)=\left(\left(-3\right)^2-9\right)\times f\left(-3\right)\)
\(\Leftrightarrow\)\(-3\times f\left(-1\right)=0\times f\left(-3\right)=0\)
\(\Leftrightarrow\)\(f\left(-1\right)=0\)
\(\Rightarrow\)x=-1 là nghiệm của f(x)
Vậy f(x) có ít nhất 3 nghiệm là x=5; x=0; x=-1
1. Cho fleft(xright)x^{2n}-x^{2n-1}+x^{2n-2}-...+x^2-x+1
gleft(xright)1-x+x^2-...+x^{2n-2}-x^{2n-1}+x^{2n}
Tính giá trị của đa thức h(x) tại x2012, biết hleft(xright)left(fleft(xright)+gleft(xright)right).left(gleft(xright)-fleft(xright)right)
2. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) ax + b với ane0, biết f(-1) 1 và f(1) -1
b) Tam thức bậc hai gleft(xright)ax^2+bx+c với ane0, biết g(-2) 9, g(-1) 2, g(1)6
3. a) Đa thức f(x) ax + b left(ane0right). Biết f(0) 0...
Đọc tiếp
1. Cho \(f\left(x\right)=x^{2n}-x^{2n-1}+x^{2n-2}-...+x^2-x+1\)
\(g\left(x\right)=1-x+x^2-...+x^{2n-2}-x^{2n-1}+x^{2n}\)
Tính giá trị của đa thức h(x) tại x=2012, biết \(h\left(x\right)=\left(f\left(x\right)+g\left(x\right)\right).\left(g\left(x\right)-f\left(x\right)\right)\)
2. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) = ax + b với \(a\ne0\), biết f(-1) = 1 và f(1) = -1
b) Tam thức bậc hai \(g\left(x\right)=ax^2+bx+c\) với \(a\ne0\), biết g(-2) = 9, g(-1) = 2, g(1)=6
3. a) Đa thức f(x) = ax + b \(\left(a\ne0\right)\). Biết f(0) = 0. Chứng minh f(x) = -f(-x) với mọi x
b) Đa thức f(x) = ax2 + bx + c \(\left(a\ne0\right)\). Biết f(1) = f(-1). Chứng minh f(x) = f(-x) với mọi x.
Tìm đa thức bậc ba f(x) biết: \(f\left(x\right)+f\left(x+1\right)=4x^3+14x^2+16x+17\)
Đặt \(f\left(x\right)=ax^3+bx^2+cx+d\)
\(\Rightarrow f\left(x+1\right)=a\left(x+1\right)^2+b\left(x+1\right)^2+c\left(x+1\right)+d\)
\(\Rightarrow f\left(x+1\right)=ax^3+\left(3a+b\right)x^2+\left(3a+2b+c\right)x+a+b+c+d\)
\(\Rightarrow f\left(x\right)+f\left(x+1\right)=2ax^3+\left(3a+2b\right)x^2+\left(3a+2b+2c\right)x+a+b+c+2d\)
Đồng nhất hệ số ta được:
\(\left\{{}\begin{matrix}2a=4\\3a+2b=14\\3a+2b+2c=16\\a+b+c+2d=17\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=4\\c=1\\d=5\end{matrix}\right.\)
Vậy \(f\left(x\right)=2x^3+4x^2+x+5\)
Đúng 0
Bình luận (0)













