Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC ( H ϵ BC ). Kẻ HE vuông góc với AB, HD vuông góc với AC
Chứng minh ED//BC
mn làm nhanh nhé, mik đang gấp lắm ạ
Cho ΔABC cân tại A. Kẻ AH vuông góc với BC (H ∈ BC ). Chứng minh rằng:
a) HB = HC
c) Kẻ HD vuông góc với AB (D ∈ AB), kẻ HE vuông góc với AC (E∈AC). Chứng minh tam giác HDE là tam giác cân.
giúp mik đi pls
mik đang cần gấp ![]()
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>DH=EH
=>ΔHDE cân tại H
Cho tam giác ABC cân tại A ,kẻ AH vuông góc với BC ( H thuộc BC )
a) Chứng minh góc BAH = góc ACH
b) Cho AH = 3cm , BC = 8cm . Tính độ dài của cạnh AC
c) Kẻ HE vuông góc với AB , HD vuông góc với AC . Chứng minh AE = AD
d) Chứng ming ED song song với BC
Giúp mình vs lm ơn , đang lm bt tết nên cần gấp ạ , xin chân thành cảm ơn :3
đề bài có lỗi ko bạn ?
a, Vì tam giác ABC cân tại A
AH là đường cao nên đồng thời là đường phân giác
=> ^BAH = ^CAH
b, Vì tam giác ABC cân tại A nên AH đồng thời là đường trung tuyến
=> HB = HC = BC/2 = 4 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{9+16}=5cm\)
c, Xét tam giác AEH và tam giác ADH ta có :
^EAH = ^DAH (cmt)
AH_chung
^AEH = ^ADH = 900
Vậy tam giác AEH = tam giác ADH ( ch - gn )
=> AE = AD ( 2 cạnh tương ứng )
d, Ta có : \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)vì AE = AD ; AB = AC
=> ED // BC
Cho tam giác ABC cân tại A kẻ AH vuông góc với BC tại H
a/Chứng minh ΔAHB =ΔAHC. Từ đó suy ra HB=HC
b/Kẻ HD vuông góc với AB(D ϵ AB), HE vuông với AC (E ϵ AC). Chứng minh ΔHDE là tam giác cân
c/Chứng minh AD=AE và DC//BC
a.Xét tam giác vuông AHB và tam giác vuông AHC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AHB = tam giác vuông AHC ( cạnh huyền. góc nhọn)
=> HB = HC ( 2 cạnh tương ứng )
b.Xét tam giác vuông ADH và tam giác vuông AEH, có:
AH: cạnh chung
góc DAH = góc EAH ( AH là đường cao cũng là đường phân giác )
Vậy tam giác vuông ADH = tam giác vuông AEH
=> HD = HE ( 2 cạnh tương ứng )
=> tam giác HDE cân tại H
c.Xét tam giác vuông AEC và tam giác vuông ADB, có:
AB = AC ( ABC cân )
góc A: chung
Vậy tam giác vuông AEC = tam giác vuông ADB ( cạnh huyền.góc nhọn)
=> AD = AE ( 2 cạnh tương ứng )
=> tam giác ADE cân tại A
=> AH vuông với DE, mà AH cũng vuông với BC
=> DE//BC ( DE ko phải DC nha bạn )
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó:ΔAHB=ΔAHC
Suy ra: HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
c: Ta có: ΔADH=ΔAEH
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Cho tam giác ABC cân tại A, kẻ AH vuông góc( \(H\in BC\))
Cho AH=3cm, BC=8cm,BH=4cm.Tính độ dài AC
Kẻ HE vuông góc với AB, HD vuông góc với AC. Chứng minh: AE=AD
Chứng minh: ED//BC
Vẽ hình dùm mik nha!!!
a) có tam giác abc cân tại a mà ah là phân giác của bac => ah cũng là đường trung truyến => bh=hc=bc/2=8/2=4cm
xét tam giác vuông ahc có \(AC^2=AH^2+HC^2=3^2+4^2=9+15=25\Rightarrow AC=5CM\)
B) xét tam giác vuông aeh và tam giác vuông adh
có ah chung ; aeh= dah ( vì tam giác abc cân mà ah là đường cao => ah là phân giác )
=> tam giác vuông aeh = tam giác vuông adh ( trường hợp cạnh huyền - góc nhọn ) => ae =ad => dpcm
c) có ae = ad ( câu a ) => tam giác aed cân => aed= aed= \(\frac{180^0-A}{2}\) (1)
có tam giác abc cân a ( đề bài ) => abc = acb = \(\frac{180^o-A}{2}\)(2)
từ (1) và (2) => aed = abc = ade=acb hay aed=abc mà 2 góc này ở vị trí so le trong
=. ed//bc
Cho tam giác ABC cân tại A kẻ AH vuông góc với BC (h thuộc BC).
a)Chứng minh góc Bah = CAH
b) Tính AC biết AH = 3cm, BC = 8cm.
c) Kẻ HE vuông góc với AB, HD vuông góc với AC. Chứng minh rằng HE = HD.
d)Chứng minh rằng ED song song với BC.
e) ọi giao điểm của AH và ED là M. Chứng minh rằng MH là phân giác của góc BAC và góc BMC.
Trả lời
a) Ta có:
AB = AE + EB
AC = AD + DC
Mà AB = AC (gt)
=> EB = DC
Xét ΔBDCΔBDC và ΔCEBΔCEB có:
EB = DC (cmt)
góc BDC = góc CEB = 900
BC là cạnh chung
Vậy: ΔBDCΔBDC = ΔCEBΔCEB (cạnh huyền - cạnh góc vuông)
b) Ta có: BC = BH + HC
=> BH = HC = BC2BC2 = 8282= 4 (cm)
Áp dụng định lí Py - ta - go vào ΔAHCΔAHC vuông tại H có:
AC2 = AH2 + HC2
AC2 = 32 + 42
AC2 = 9 + 16
AC2 = 25
AC = 25−−√25= 5 (cm)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC(H thuộc BC) .Từ H kẻ HD vuông góc AB(D thuộc BC),từ H kẻ HE vuông góc AC(E thuộc AC) .chứng minh tam giác HED là tam giác cân
Câu 8 Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H ![]() BC)
BC)
a) Chứng minh HB = HC
b) Chứng minh góc BAH =góc CAH
c) Kẻ HD vuông góc với AB (D thuộc AB). Kẻ HE vuông góc với AC (E ![]() AC). Chứng minh tam giác HDE là tam giác cân
AC). Chứng minh tam giác HDE là tam giác cân
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
Cho tam giác ABC cân có AB=AC=5cm, BC= 8cm. Kẻ AH vuông góc với BC (H thuộc BC).
a. Chứng minh HB = HC và góc BAH = góc CAH
b. Kẻ HD vuông góc với AB(D thuộc AB) Kẻ HE vuông góc với Ac (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
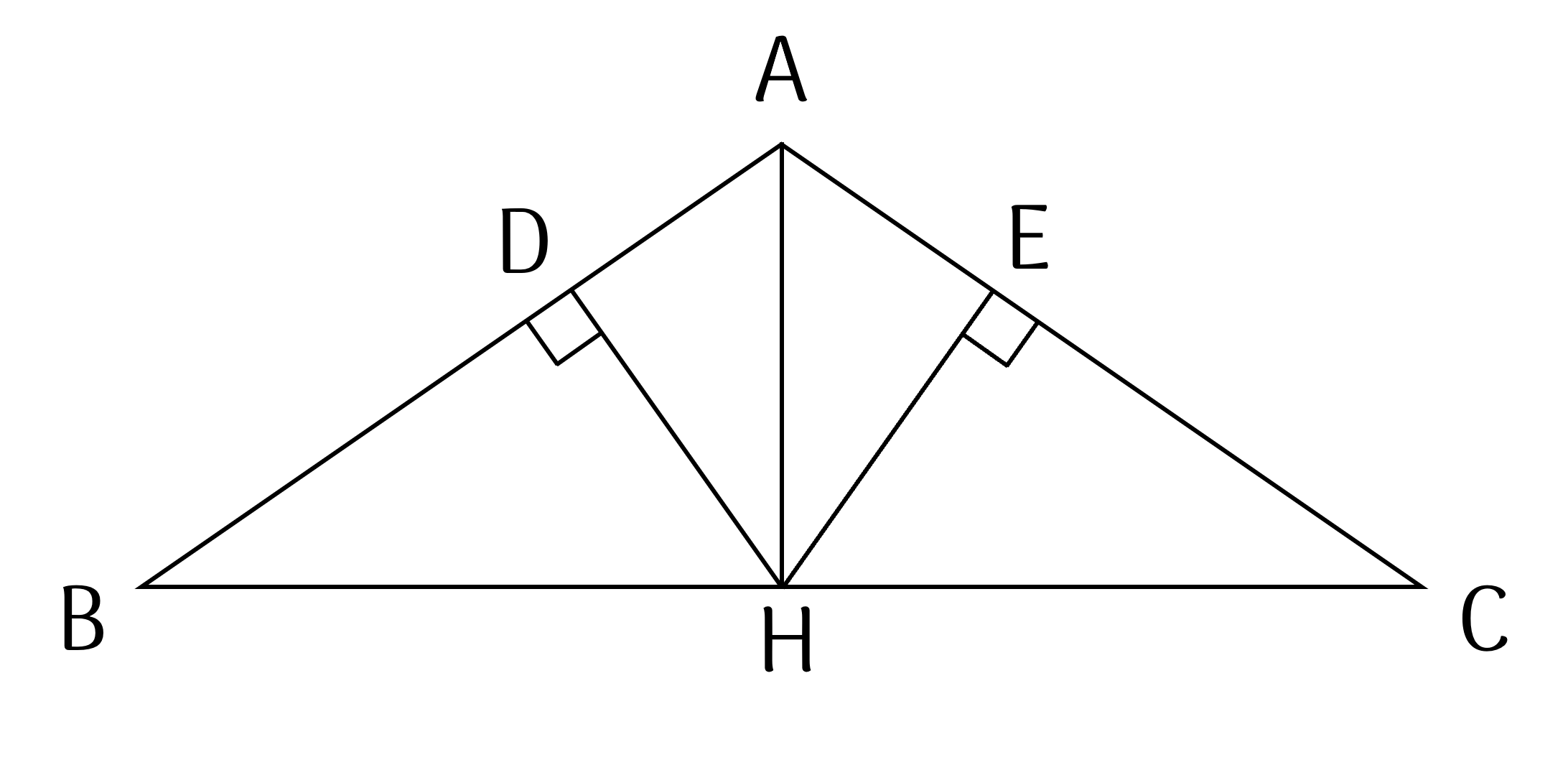
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.
Cho △ABC cân tại A. Kẻ AH vuông góc với BC (H ϵ BC)
1) Chứng minh : △AHB = △AHC
2) Tính AH biết rằng AB = 10cm, BC = 16cm ?
3) Kẻ AD vuông góc AB ( D ϵ AB ); HE vuông góc với BC ( E ϵ AC ). CMR: △HDE là tam giác cân.
4) CMR : \(^{AH^2+BD^2=AE^2+BH^2}\)
1) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
2) Ta có: ΔAHB=ΔAHC(cmt)
nên HB=HC(hai cạnh tương ứng)
mà HB+HC=BC(H nằm giữa B và C)
nên \(HB=HC=\dfrac{BC}{2}=\dfrac{16}{2}=8\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AH^2=AB^2-BH^2=10^2-8^2=36\)
hay AH=6(cm)
Vậy: AH=6cm
Có phải bài này trong đề kiểm tra hả bạn ?