Bác học lớp 9 phải ko bài này khá đơn giản mình thấy ai cũng làm đc chỉ cần độg não thui chứ bác hỏi thế rùi vô phòng thi thì sao lớp 9 phải tự học thui

cần gấp ae ơi

a) Xét tứ giác AIHK có 3 góc vuông nên AIHK là hình chữ nhật.

b) Do D và H đối xứng nhau qua AB nên AI cũng là phân giác góc DAH.

Vậy thì \(\widehat{BAH}=\frac{\widehat{DAH}}{2}\)

Tương tự \(\widehat{CAH}=\frac{\widehat{EAH}}{2}\)

Vậy nên \(\widehat{DAE}=2\left(\widehat{BAH}+\widehat{CAH}\right)=180^o\)

Vậy D, A, E thẳng hàng.

c) Ta có ngay do D, H đối xứng với nhau qua AB nên BH = BD

Tương tự ta có HC = EC

Vậy nên C = BH + HC = BD + EC.

d) Ta thấy : \(\Delta ADI=\Delta AHI\Rightarrow S_{ADI}=S_{AHI}\)

Tương tự \(S_{AKH}=S_{AKE}\Rightarrow S_{AIHK}=S_{DIA}+S_{AKE}\)

\(\Rightarrow S_{AIHK}=\frac{1}{2}S_{DHE}\)

Vậy \(S_{DHE}=2a\left(đvdt\right)\)

Bài 12:

:v Mình sửa P là trung điểm của EG

a) Ta có: \(\widehat{EAC}=\widehat{EAB}+\widehat{BAC}=90^0+\widehat{BAC}\)

\(\widehat{GAB}=\widehat{GAC}+\widehat{BAC}=90^0+\widehat{BAC}\)

\(\Rightarrow\widehat{EAC}=\widehat{GAB}\)

Xét tam giác EAC và tam giác BAG có:

\(\hept{\begin{cases}EA=AB\\\widehat{EAC}=\widehat{GAB}\left(cmt\right)\\AG=AC\end{cases}}\Rightarrow\Delta EAC=\Delta BAG\left(c-g-c\right)\)

\(\Rightarrow CE=BG\)( 2 cạnh t. ứng )

+) Gọi O là giao điểm của EC và BG, Gọi I là giao điểm của AC và BG 

Vì \(\Delta EAC=\Delta BAG\left(cmt\right)\)

\(\Rightarrow\widehat{ACE}=\widehat{AGB}\)

Vì tam giác AIG vuông tại A nên \(\widehat{I1}+\widehat{AGB}=90^0\)(2 góc phụ nhau )

Mà \(\widehat{ACE}=\widehat{AGB}\left(cmt\right),\widehat{I1}=\widehat{I2}\)( 2 góc đối đỉnh )

\(\Rightarrow\widehat{I2}+\widehat{ACE}=90^0\)

Xét tam giác OIC có \(\widehat{I2}+\widehat{ACE}+\widehat{IOC}=180^0\left(dl\right)\)

\(\Rightarrow\widehat{IOC}=90^0\)

\(\Rightarrow BG\perp EC\)

b) Vì ABDE là hình vuông (gt)

\(\Rightarrow EB\)cắt AD tại Q là trung điểm của mỗi đường (tc)

Xét tam giác EBC có Q là trung điểm của EB (cmt) , M là trung điểm của BC (gt)

\(\Rightarrow QM\)là đường trung bình của tam giác EBC

\(\Rightarrow QM=\frac{1}{2}EC\left(tc\right)\)

CMTT: \(PN=\frac{1}{2}EC;QP=\frac{1}{2}BG,MN=\frac{1}{2}BG\)

Mà EC=BG (cm câu a )

\(\Rightarrow QM=MN=NP=PQ\)

Xét tứ giác MNPQ  có \(QM=MN=NP=PQ\left(cmt\right)\)

\(\Rightarrow MNPQ\)là hình thoi ( dhnb ) (1)

CM: MN//BG , QM//EC ( dựa vào đường trung bình tam giác )

Mà \(BG\perp EC\left(cmt\right)\)

\(\Rightarrow MN\perp MQ\)

\(\Rightarrow\widehat{QMN}=90^0\)(2)

Từ (1) và (2) \(\Rightarrow MNPQ\) là hình vuông ( dhnb ) 

\(\)

Bài 11:

a) Ta có: \(\widehat{HAD}+\widehat{HAE}=90^0+90^0=180^0\)

\(\Rightarrow\widehat{DAE}=180^0\)

\(\Rightarrow D,A,E\)thẳng hàng

b) Vì AHBD là hình chữ nhật (gt)

\(\Rightarrow AB\)cắt DH tại trung điểm mỗi đường (tc) và AB=DH(tc)

Mà P là trung điểm của AB (gt)

\(\Rightarrow P\)là trung điểm của DH  (1)

\(\Rightarrow PH=\frac{1}{2}DH,PA=\frac{1}{2}AB\)kết hợp với AB=DH (cmt)

\(\Rightarrow PH=PA\)

\(\Rightarrow P\in\)đường trung trục của AH

CMTT Q thuộc đường trung trực của AH

\(\Rightarrow PQ\)là đường trung trực của AH

c)  Từ (1) => P thuộc DH

=> D,P,H thẳng hàng

d) Vì ABCD là hình chữ nhật (gt)

=> DH là đường phân giác của góc BHA (tc) mà góc BHA= 90 độ

=> góc DHA= 45 độ

CMTT AHE =45 độ

=> góc DHA+ góc AHE=90 độ

Hay góc DHE=90 độ

=> DH vuông góc với HE

Bài 7 failed nha bạn bạn xem lại đề 

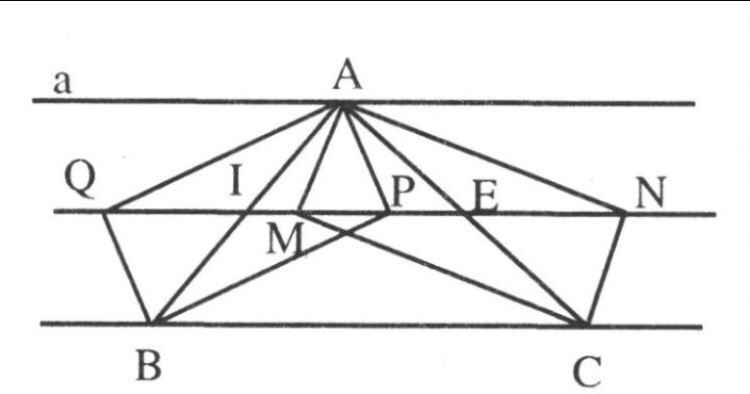
a. Vì BQ và BP là p/g ngoài và trong của \(\widehat{ABC}\) nên \(BP\bot BQ\)

Lại có \(AQ\bot BQ, AP\bot BP\) nên AQPB là hcn

Cmtt ta được AMCN cũng là hcn

b. Gọi I là giao 2 đường chéo AB và PQ của hcn AQBP

\(\Rightarrow IB=IA=IC\\ \Rightarrow\widehat{IPB}=\widehat{IBP}=\widehat{PBC}\left(BP\text{ là p/g}\right)\)

Mà 2 góc này ở vị trí slt nên IP//BC

\(\Rightarrow P,Q\) nằm trên đtb của \(\Delta ABC\)

Tương tự M,N cũng nằm trên đtb \(\Delta ABC\)

Vậy M,N,Q,P thẳng hàng

a: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}x^2=2x+3\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{3;-1\right\}\\y\in\left\{9;1\right\}\end{matrix}\right.\)

b: A(3;9) B(-1;1)

\(OA=\sqrt{3^2+9^2}=3\sqrt{10}\)

\(OB=\sqrt{\left(-1\right)^2+1^2}=\sqrt{2}\)

\(AB=\sqrt{\left(-4\right)^2+\left(-8\right)^2}=4\sqrt{5}\)

\(\Leftrightarrow P=\dfrac{3\sqrt{10}+\sqrt{2}+4\sqrt{5}}{2}\)

\(S=\sqrt{\dfrac{3\sqrt{10}-\sqrt{2}+4\sqrt{5}}{2}\cdot\dfrac{3\sqrt{10}+\sqrt{2}+4\sqrt{5}}{2}\cdot\dfrac{-3\sqrt{10}+\sqrt{2}+4\sqrt{5}}{2}\cdot\dfrac{3\sqrt{10}+\sqrt{2}-4\sqrt{5}}{2}}\)

\(=\sqrt{\dfrac{576}{16}}=\dfrac{24}{4}=6\)