Bạn hãy phân tích lực tác dụng thành hai thành phần: thành phần vuông góc với phương dịch chuyển và thành phần trùng với phương dịch chuyển để lập luận rút ra biểu thức tính công.

Những câu hỏi liên quan
Giúp mình với ạ Một vật có trọng lượng P=20N đặt trên một mặt phẳng nghiêng hợp với phương nằm nang một góc 30° a, vẽ hình phân tích trọng lực ra hai lực thành phần vuông góc và song song với mặt phẳng nghiêng b, tính độ lớn của mỗi lực thành phần đó
qua khổ thơ đầu em hãy viết đoạn văn (khoảng 12 câu) theo phương pháp lập luận diễn dịch, phân tích đoạn thơ trên để thấy được cơ sở bền chặt hình thành nên tình đồng chí. Trong đoạn có sử dụng thành phần biệt lập phụ chú và phép nối để liên kế
Khi khảo sát dao động của con lắc đơn với biên độ góc nhỏ, ta phân tích trọng lực thành hai thành phần:
P
1
theo phương của sợi dây và
P
2
vuông góc với sợi dây thì A.
P
1
luôn cân bằng với lực căng sợi dây do vật không chuyển động theo phương của sợi dây. B.
P
1
Hai thành phần này không đổi theo thời gian. C....
Đọc tiếp
Khi khảo sát dao động của con lắc đơn với biên độ góc nhỏ, ta phân tích trọng lực thành hai thành phần: P 1 theo phương của sợi dây và P 2 vuông góc với sợi dây thì
A. P 1 luôn cân bằng với lực căng sợi dây do vật không chuyển động theo phương của sợi dây.
B. P 1 Hai thành phần này không đổi theo thời gian.
C. P 1 có độ lớn tỉ lệ thuận với góc lệch của sợi dây và phương thẳng đứng.
D. P 1 nhỏ hơn hoặc bằng lực căng sợi dây.
Chọn D.
Lực hướng tâm: R - P 1 = m v 2 l > 0 ⇒ R > P 1
Đúng 0
Bình luận (0)
Một cậu bé đang kéo thùng hàng trên mặt đất bằng sợi dây hợp với phương ngang một góc 300 (Hình 13.9). hãy tìm độ lớn lực kéo thành phần trên hai phương vuông góc và song song với mặt đất, biết độ lớn lực kéo cậu bé tác dụng lên dây là 12 N.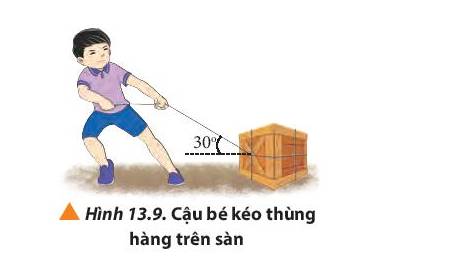
Một cậu bé đang kéo thùng hàng trên mặt đất bằng sợi dây hợp với phương ngang một góc 300 (Hình 13.9). hãy tìm độ lớn lực kéo thành phần trên hai phương vuông góc và song song với mặt đất, biết độ lớn lực kéo cậu bé tác dụng lên dây là 12 N.
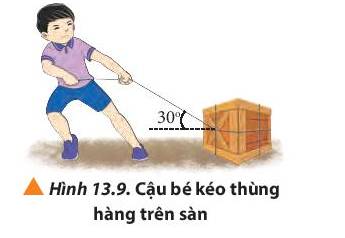
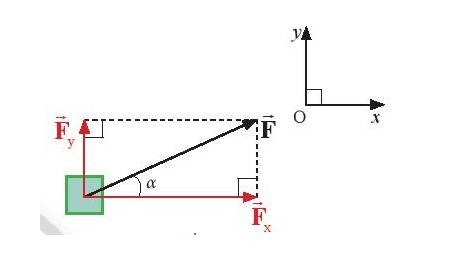
Ta có F = 12 N, α = 300
Độ lớn lực thành phần:
+ Fx = F.cosα = 12.cos300 = \(6\sqrt 3 \)(N).
+ Fy = F.sinα = 12.sin300 = 6 (N).
Đúng 0
Bình luận (0)
Phân tích lực F thành hai lực thành phần F1 và F2 vuông góc với nhau. Biết độ lớn:
A. 40N
B. 80N
C. 160N
D. 640N
Chọn đáp án B
F1 và F2 là hai lực vuông góc với nhau nên ta có:

Đúng 0
Bình luận (0)
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,0^o. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.a) Vẽ giản đồ vectơ lực tác dụng lên thùng.b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m...
Đọc tiếp
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc \(30,0^o\). Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.
a) Vẽ giản đồ vectơ lực tác dụng lên thùng.
b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.
c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.
d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là \(2,00m\)/s2. Bỏ qua lực cản của không khí lên thùng.
a)
Giản đồ vectơ các lực tác dụng lên thùng hàng:

b)
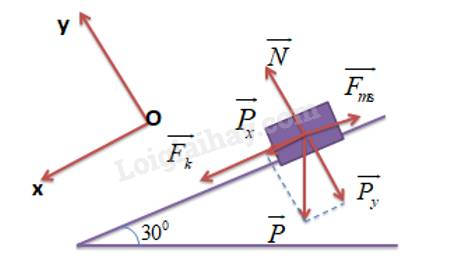
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.
Đúng 0
Bình luận (0)
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,00. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.a) Vẽ giản đồ vectơ lực tác dụng lên thùng.b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m...
Đọc tiếp
Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,00. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.
a) Vẽ giản đồ vectơ lực tác dụng lên thùng.
b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.
c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.
d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m/s2. Bỏ qua lực cản của không khí lên thùng.
Lập phương trình quỹ đạo của chuyển động ném ngang, các công thức tính thời gian chuyển động thành phần.
Khi vật M chuyển động thì các hình chiếu Mx và My của nó trên hai trục toạ độ cũng chuyển động theo
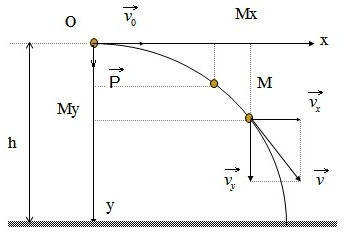
Thời gian chuyển động tổng hợp bằng thời gian chuyển động thành phần theo trục Oy. Suy ra thời gian chuyển động ném ngang của vật bằng thời gian rơi rự do từ cùng một độ cao.
\(t=\sqrt{\dfrac{2h}{y}}\)
Đúng 0
Bình luận (0)
Khi vật M chuyển động thì các hình chiếu Mx và My của nó trên hai trục toạ độ cũng chuyển động theo
Thời gian chuyển động tổng hợp bằng thời gian chuyển động thành phần theo trục Oy. Suy ra thời gian chuyển động ném ngang của vật bằng thời gian rơi rự do từ cùng một độ cao.

Đúng 0
Bình luận (0)















