Cho tam giác MNK vuông tại M . Biết MN=9 cm ; MK = 12 cm
a, Tính NK
b, Trên tia đối của tia MN lấy điểm I sao cho MN=MI . CM : tam giác KNI cân
c, Từ M vẽ MA vuông góc với NK tại A , MB vuông góc với IK tại B . CM tam giác MAK=MBK .Và AB// NI
Cho tam giác MNK vuông tại M . Biết MN = 9 cm , MK = 12 cm
a ) Tính NK
b) Trên tia đối của tia MN lấy điểm I sao cho MN = MI . CM tam giác KNI cân
c ) Từ M vẽ MA vuông góc với NK tại A , MB vuông GÓC VỚI ik tại B
d) CM : AB // NI
câu a) áp dụng định lý Pytago mà làm
b) ta có: \(MN=MI\)và \(MK\perp NI\)
\(\Rightarrow MK\) là đường trung trực \(\Delta KNI\)
xét \(\Delta KNM\)và \(\Delta KIM\) có:
\(KM\)chung
\(\widehat{KMN}=\widehat{KMI}\) \(=90^0\)
\(MN=MI\)
\(\Rightarrow\Delta KNM=\Delta KIM\) ( C.G.C)
\(\Rightarrow KN=KI\)
\(\Rightarrow\Delta KNI\)cân
câu a) áp dụng định lý Pytago mà làm b) ta có: MN = MI và MK⊥NI
⇒MK là đường trung trực ΔKNI xét ΔKNMvà ΔKIM có:
KMchung = = 90 0
MN = MI
⇒ΔKNM = ΔKIM ( C.G.C)
⇒KN = KI ⇒ΔKNI cân
mk nghĩ vậy
:3
cho tam giác MNP vuông tại M,góc N=60 độ ,MN=8cm, MP=8cm.Tia phân giác MNP cắt MP tại K. Kẻ KH vuông với NP tại H
a) Tính NP
b) Cm Tam giác MNK=HNK
c) Tam giác MNH là tam giác gì? Why?
giúp mình với
cho tam giác MNP vuông tại M,góc N=60 độ ,MN=8cm, MP=8cm.Tia phân giác MNP cắt MP tại K. Kẻ KH vuông với NP tại H
a) Tính NP
b) Cm Tam giác MNK=HNK
c) Tam giác MNH là tam giác gì? Why?
giúp mình với
cho tam giác ABC vuông tại A , tia phân giác của ABC cắt AC tại M . Gọi N là hình chiếu của M trên BC . a, CM tam giác ABM = tam giác NBM và MB là tia phân giác của AMN . b, Vẽ NK // BM [ K thuộc MC ] . CM BMN = MNK và tam giác MNK cân. Có vẽ hình nha mọi người
a: Xét ΔABM vuông tại A và ΔNBM vuông tại N có
BM chung
\(\widehat{ABM}=\widehat{NBM}\)
Do đó: ΔABM=ΔNBM
=>\(\widehat{AMB}=\widehat{NMB}\)
=>MB là phân giác của góc AMN
b: Ta có: NK//BM
=>\(\widehat{BMN}=\widehat{KNM}\)(hai góc so le trong) và \(\widehat{MKN}=\widehat{AMB}\)(hai góc đồng vị)
mà \(\widehat{NMB}=\widehat{AMB}\)
nên \(\widehat{KNM}=\widehat{MKN}\)
=>ΔMKN cân tại M
CHO TAM GIÁC MNP VUÔNG TẠI N(NM<NP), TIA PHÂN GIÁC CỦA GÓC M CẮT CẠNH NP TẠI K.TRÊN MP LẤY ĐIỂM I SAO CHO MN=MI
A) CHỨNG MINH TAM GIÁC MNK = TAM GIÁC MIK. SUY RA TAM GIÁC NKI CÂN
B) TIA MN CẮT TIA IK TẠI E. CHỨNG MNH MK VUÔNG GÓC EP
a: Xét ΔMNK và ΔMIK có
MN=MI
góc NMK=góc IMK
MK chung
=>ΔMNK=ΔMIK
=>KN=KI
=>ΔKNI cân tại K
b: ΔMNK=ΔMIK
=>góc MIK=góc MNK=90 độ
b: Xét ΔMEP có
EI,PN là đường cao
EI cắt PN tại K
=>K là trực tâm
=>MK vuông góc EP
Cho tam giác MNK vuông tại N có MN = 6cm, NK = 8cm
a) Tính MK
b) So sánh các góc của tam giác MNK
c) Cho góc K = 40 độ. Tính góc M
d) Biết NI là đường trung tuyến của tam giácMNK . G là trọng tâm. Tính NG
cho tam giác ABC vuông tại A , tia phân giác của ABC cắt AC tại M . Gọi N là hình chiếu của M trên BC . a, CM tam giác ABM = tam giác NBM và MB là tia phân giác của AMN . b, Vẽ NK // BM [ K thuộc MC ] . CM BMN = MNK và MNK cân . Có vẽ hình nha mọi người
a: Xét ΔABM vuông tại A và ΔNBM vuông tại N có
BM chung
\(\widehat{ABM}=\widehat{NBM}\)
Do đó: ΔABM=ΔNBM
Suy ra: \(\widehat{AMB}=\widehat{NMB}\)
hay MB là tia phân giác của góc AMN
b: Ta có: MK//BM
nên \(\widehat{BMN}=\widehat{MNK}\)
Bài 4: Cho tam giác MNK vuông tại M. Biết MN = 9cm; MK = 12cm.
a.Tính NK.
b. Trên tia đối của tia MN lấy điểm I sao cho MN = MI. Chứng minh: ΔKNI cân.
c. Từ M vẽ tại A, tại B. Chứng minh ΔMAK = ΔMBK.
d. Chứng minh: AB // NI.
giúp mik với
a: NK=15cm
b: Xét ΔKNI có
KM là đường cao
KM là đường trung tuyến
Do đó: ΔKNI cân tại K
c: Xét ΔMAK vuông tại A và ΔMBK vuông tại B có
KM chung
\(\widehat{AKM}=\widehat{BKM}\)
Do đó: ΔMAK=ΔMBK
d: Ta có: ΔMAK=ΔMBK
nên KA=KB
Xét ΔKIN có KB/KI=KA/KN
nên AB//IN
Cho tam giác ABC vuông tại A tia phân giác của ABC cát AC tại M . gọi N là hình chiếu của M trên BC
CM tam giác ABM = NBM và MB là tia phân giác của AMN
Vẽ NK song song BM ( K thuộc MC ) . CM BMN = MNK và tam giác MNK cân
Xét \(\Delta ABM\) và \(\Delta NBM\)
\(\widehat{MAB}=\widehat{MNB}=90^o\)
\(MB\) chung
\(\widehat{MBA}=\widehat{MBN}\) (vì \(BM\) là tia phân giác của \(\widehat{ABN}\))
suy ra: \(\Delta ABM=\Delta NBM\) (Cạnh huyền-góc nhọn)
\(\Rightarrow\widehat{AMB}=\widehat{NMB}\) (Hai góc tương ứng)
\(\Rightarrow MB\) là tia phân giác của \(\widehat{AMN}\)
Vì \(NK\)//\(BM\) nên \(\widehat{BMN}=\widehat{MNK}\) (hai góc so le trong)
Và \(\widehat{BMA}=\widehat{NKM}\) (đồng vị)
Mà \(\widehat{AMB}=\widehat{NMB}\) (cmt)
Suy ra: \(\widehat{MNK}=\widehat{NKM}\) \(\Rightarrow\Delta MNK\) cân tại \(M\) (đpcm)
a: Xét ΔBAM vuông tại A và ΔBNM vuông tại N có
BM chung
góc ABM=góc NBM
=>ΔBAM=ΔBNM
=>góc AMB=góc NMB
=>MB là phân giác của góc AMN
b: NK//BM
=>góc BMN=góc KNM
=>góc KNM=góc AMB
=>góc MNK=góc MKN
=>ΔKMN cân tại M
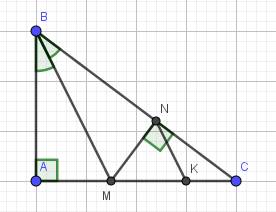
a) Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta NBM\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{NBM}\) (BM là tia phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta ABM=\Delta NBM\) (cạnh huyền - góc nhọn)
\(\Rightarrow\widehat{AMB}=\widehat{NMB}\) (hai góc tương ứng)
\(\Rightarrow MB\) là tia phân giác của \(\widehat{AMN}\)
b) Do NK // BM
\(\Rightarrow\widehat{BMN}=\widehat{MNK}\) (so le trong)
\(\widehat{NKM}=\widehat{AMB}\) (đồng vị)
Mà \(\widehat{AMB}=\widehat{BMN}\) (cmt)
\(\Rightarrow\widehat{MNK}=\widehat{NKM}\)
\(\Delta MNK\) có \(\widehat{MNK}=\widehat{NKM}\) (cmt)
\(\Rightarrow\Delta MNK\) cân tại M