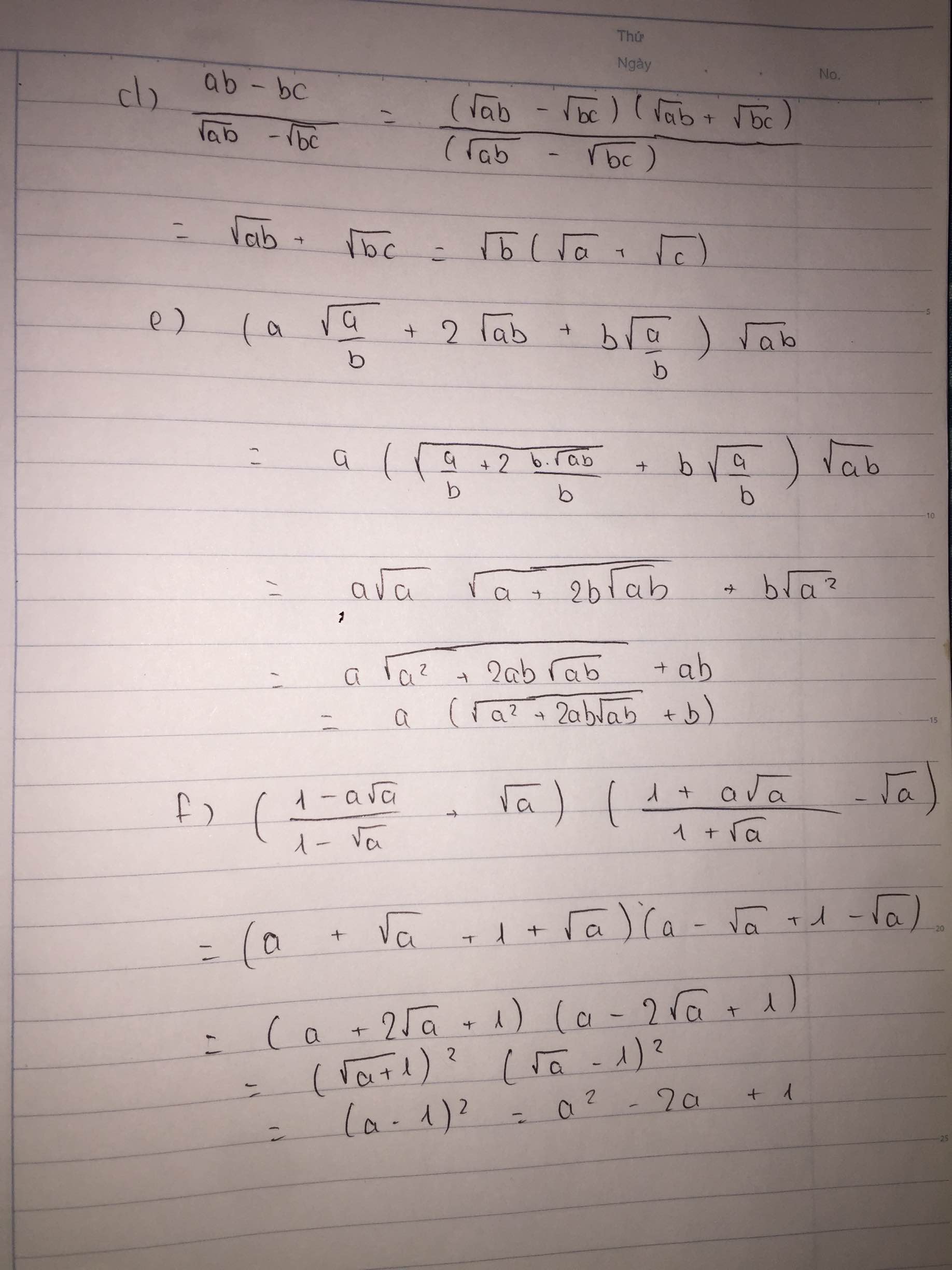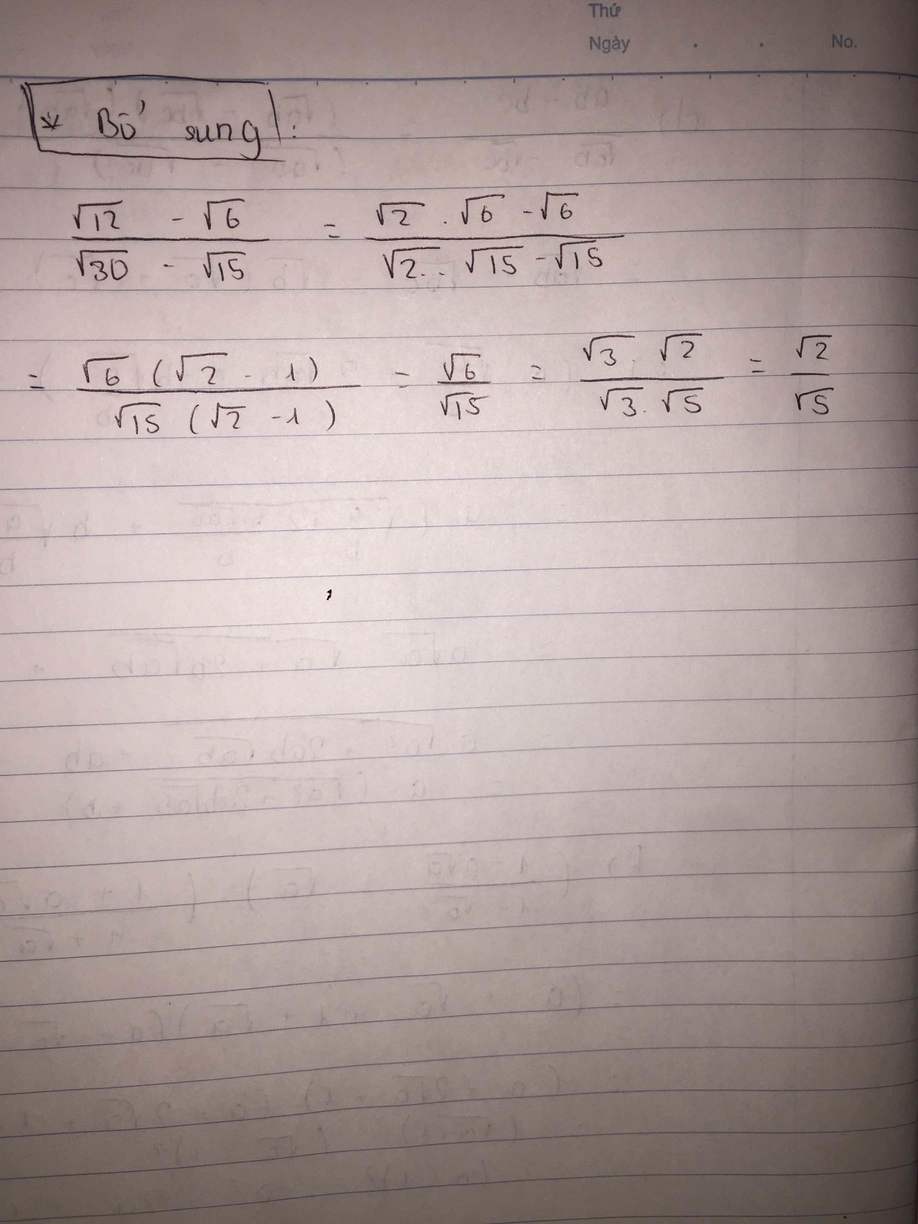giúp mình câu a b c e f nhé .Cảm ơn ạ!

Những câu hỏi liên quan
giúp mình câu d, e,f, h đi ạ, mình cảm ơn
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
Đúng 4
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn (O;R). Vẽ 2 đường cao BE và CF cắt nhau tại Ha) C/m A, E, H, F thuộc (I), xác định tâm Ib) C/m B, E, F, C thuộc (J), xác định tâm Jc) C/m IJ vuông góc EFd) Vẽ đường kính AM của (O), C/m H, I, M thẳng hàngCác bạn giúp mình gấp nhé, mình cảm ơn nhiều. Ai gửi câu trả lời nhanh và đúng nhất mình sẽ tick ạ. CẢM ƠN TẤT CẢ CÁC BẠN
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn (O;R). Vẽ 2 đường cao BE và CF cắt nhau tại H
a) C/m A, E, H, F thuộc (I), xác định tâm I
b) C/m B, E, F, C thuộc (J), xác định tâm J
c) C/m IJ vuông góc EF
d) Vẽ đường kính AM của (O), C/m H, I, M thẳng hàng
Các bạn giúp mình gấp nhé, mình cảm ơn nhiều. Ai gửi câu trả lời nhanh và đúng nhất mình sẽ tick ạ. CẢM ƠN TẤT CẢ CÁC BẠN
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp e vs. Câu a, b, c thồi nhé. E cảm ơn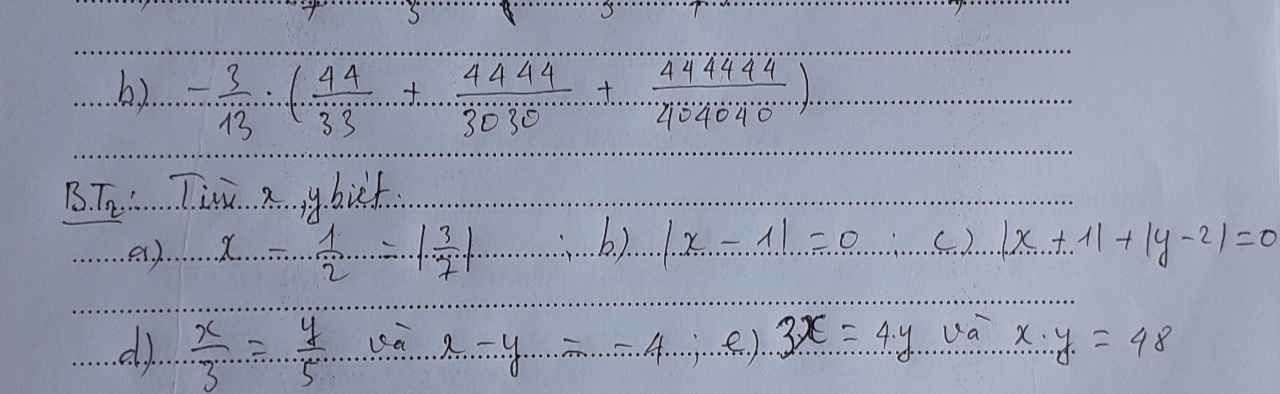
a) Ta có: \(x-\dfrac{1}{2}=\left|\dfrac{3}{7}\right|\)
nên \(x-\dfrac{1}{2}=\dfrac{3}{7}\)
hay \(x=\dfrac{3}{7}+\dfrac{1}{2}=\dfrac{6}{14}+\dfrac{7}{14}=\dfrac{13}{14}\)
b) Ta có: |x-1|=0
nên x-1=0
hay x=1
c) Ta có: \(\left|x+1\right|\ge0\forall x\)
\(\left|y-2\right|\ge0\forall y\)
Do đó: \(\left|x+1\right|+\left|y-2\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=-1 và y=2
Đúng 1
Bình luận (0)
d) Ta có: \(\dfrac{x}{3}=\dfrac{y}{5}\)
mà x-y=-4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{-4}{-2}=2\)
Do đó: x=6; y=10
e) Ta có: 3x=4y
nên \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}\)
Đặt \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k\\y=\dfrac{1}{4}k\end{matrix}\right.\)
Ta có: xy=48
nên \(\dfrac{1}{3}k\cdot\dfrac{1}{4}k=48\)
\(\Leftrightarrow k^2\cdot\dfrac{1}{12}=48\)
\(\Leftrightarrow k^2=48\cdot12=576\)
hay \(k\in\left\{24;-24\right\}\)
Trường hợp 1: k=24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot24=8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot24=6\end{matrix}\right.\)
Trường hợp 2: k=-24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot\left(-24\right)=-8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot\left(-24\right)=-6\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a, Ta có
x- \(\dfrac{1}{2}\)= \(\left|\dfrac{3}{7}\right|\)
⇒ x- \(\dfrac{1}{2}\)= \(\dfrac{3}{7}\)
⇒ x= \(\dfrac{13}{14}\)
Vậy...
b, \(\left|x-1\right|\)= 0
Ta có:
\(\left|x-1\right|\) \(\ge\) 0 với \(\forall\) x
Dấu bằng xảy ra khi:
x- 1= 0
⇒ x= 1
Vậy....
c, \(\left|x+1\right|+\left|y-2\right|=0\)
Ta có:
\(\left|x+1\right|\ge0\) với ∀ x
\(\left|y-2\right|\ge0\) với \(\forall\) y
\(\Rightarrow\)\(\left|x+1\right|\ge0\) + \(\left|y-2\right|\ge0\) ≥ 0 với \(\forall x,y\)
Dấu bằng xảy ra khi:
\(\left\{{}\begin{matrix}\left|x+1\right|=0\\\left|y-2\right|=0\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x+1=0\\y-2=0\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
Vậy.....
Đúng 0
Bình luận (0)
Mọi người ơi, giúp em câu d, e, f, b với ạ. Rút gọn.Em cảm ơn nhiều ạ!!
Đọc tiếp
Mọi người ơi, giúp em câu d, e, f, b với ạ. Rút gọn.Em cảm ơn nhiều ạ!!
Mọi người ơi giúp mình bài này nhé mình đang cần rất gấp. Mình cảm ơn mọi người ạ!
Cho ∆ABC và các điểm D,E,F thuộc BC,AC,AB sao. Cho AD,BE,CF đồng quy. Từ E,F kẻ các đường thẳng song song AD cắt BC lần lượt tại N và M.CMR:AD,ME,NF đồng quy. Mình xin cảm ơn mọi người rất nhiều ạ!
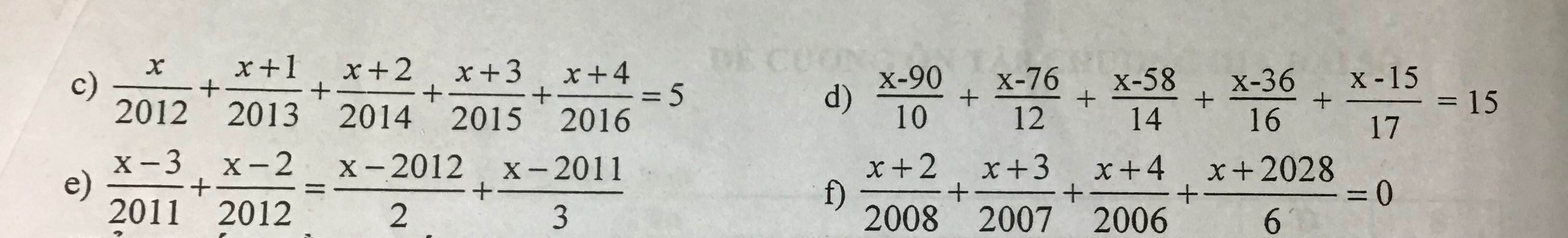 Giúp mình d,e,f với ạ !!!! Mình cảm ơn
Giúp mình d,e,f với ạ !!!! Mình cảm ơn
c: \(\Leftrightarrow\dfrac{x}{2012}-1+\dfrac{x+1}{2013}-1+\dfrac{x+2}{2014}-1+\dfrac{x+3}{2015}-1+\dfrac{x+4}{2016}-1=0\)
=>x-2012=0
hay x=2012
d: \(\Leftrightarrow\dfrac{x-90}{10}-1+\dfrac{x-76}{12}-2+\dfrac{x-58}{14}-3+\dfrac{x-36}{16}-4+\dfrac{x-15}{17}-5=0\)
=>x-100=0
hay x=100
Đúng 1
Bình luận (0)

Giúp mình câu f với ạ, mình cảm ơn
a: \(A=\dfrac{x}{x-4}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Đúng 0
Bình luận (1)
b: Thay x=36 vào biểu thức \(\dfrac{\sqrt{x}}{\sqrt{x}-2}\), ta có
\(\Rightarrow\dfrac{\sqrt{36}}{\sqrt{36}-2}\Rightarrow\dfrac{6}{6-2}\Rightarrow\dfrac{6}{4}\Rightarrow\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Tiếp của anh Nguyễn Lê Phước Thịnh:
b. Thay x = 36 vào A, ta được:
A = \(\dfrac{\sqrt{36}}{\sqrt{36}-2}=\dfrac{6}{6-2}=\dfrac{6}{4}=\dfrac{3}{2}\)
c. Ta có:
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}=-\dfrac{1}{3}\left(ĐK:x\ge0;x\ne2\right)\)
<=> \(-3\sqrt{x}=\sqrt{x}-2\)
<=> \(2=4\sqrt{x}\)
<=> \(\sqrt{x}=\dfrac{1}{2}\)
<=> \(x=\dfrac{1}{4}\left(TM\right)\)
e. Ta có:
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=-2\)
<=> \(\dfrac{\sqrt{x}}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=-2\)
<=> \(\dfrac{\sqrt{x}}{\sqrt{x}+1}=-2\)
<=> \(\sqrt{x}=-2\left(\sqrt{x}+1\right)\)
<=> \(\sqrt{x}=-2\sqrt{x}-2\)
<=> \(\sqrt{x}+2\sqrt{x}=-2\)
<=> \(3\sqrt{x}=-2\)
<=> \(\sqrt{x}=\dfrac{-2}{3}\)
<=> \(x=\dfrac{4}{9}\left(TM\right)\)
Đúng 0
Bình luận (0)
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
Đúng 1
Bình luận (0)