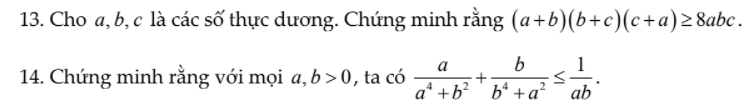a: \(A=\dfrac{x}{x-4}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b: Thay x=36 vào biểu thức \(\dfrac{\sqrt{x}}{\sqrt{x}-2}\), ta có
\(\Rightarrow\dfrac{\sqrt{36}}{\sqrt{36}-2}\Rightarrow\dfrac{6}{6-2}\Rightarrow\dfrac{6}{4}\Rightarrow\dfrac{3}{2}\)
Tiếp của anh Nguyễn Lê Phước Thịnh:
b. Thay x = 36 vào A, ta được:
A = \(\dfrac{\sqrt{36}}{\sqrt{36}-2}=\dfrac{6}{6-2}=\dfrac{6}{4}=\dfrac{3}{2}\)
c. Ta có:
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}=-\dfrac{1}{3}\left(ĐK:x\ge0;x\ne2\right)\)
<=> \(-3\sqrt{x}=\sqrt{x}-2\)
<=> \(2=4\sqrt{x}\)
<=> \(\sqrt{x}=\dfrac{1}{2}\)
<=> \(x=\dfrac{1}{4}\left(TM\right)\)
e. Ta có:
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=-2\)
<=> \(\dfrac{\sqrt{x}}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=-2\)
<=> \(\dfrac{\sqrt{x}}{\sqrt{x}+1}=-2\)
<=> \(\sqrt{x}=-2\left(\sqrt{x}+1\right)\)
<=> \(\sqrt{x}=-2\sqrt{x}-2\)
<=> \(\sqrt{x}+2\sqrt{x}=-2\)
<=> \(3\sqrt{x}=-2\)
<=> \(\sqrt{x}=\dfrac{-2}{3}\)
<=> \(x=\dfrac{4}{9}\left(TM\right)\)











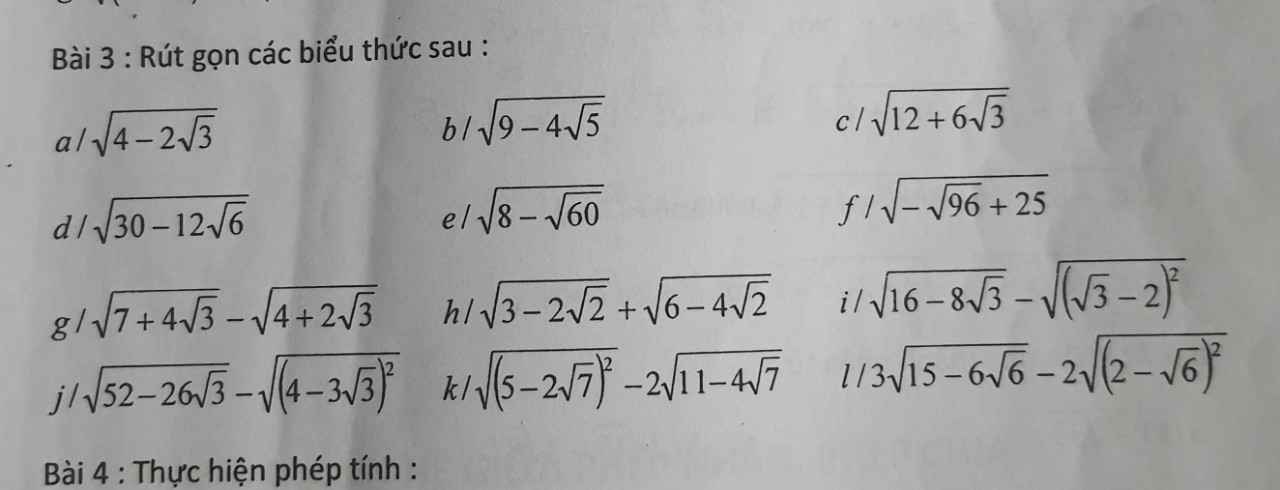



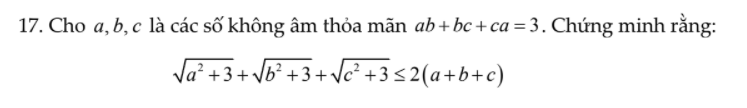 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.

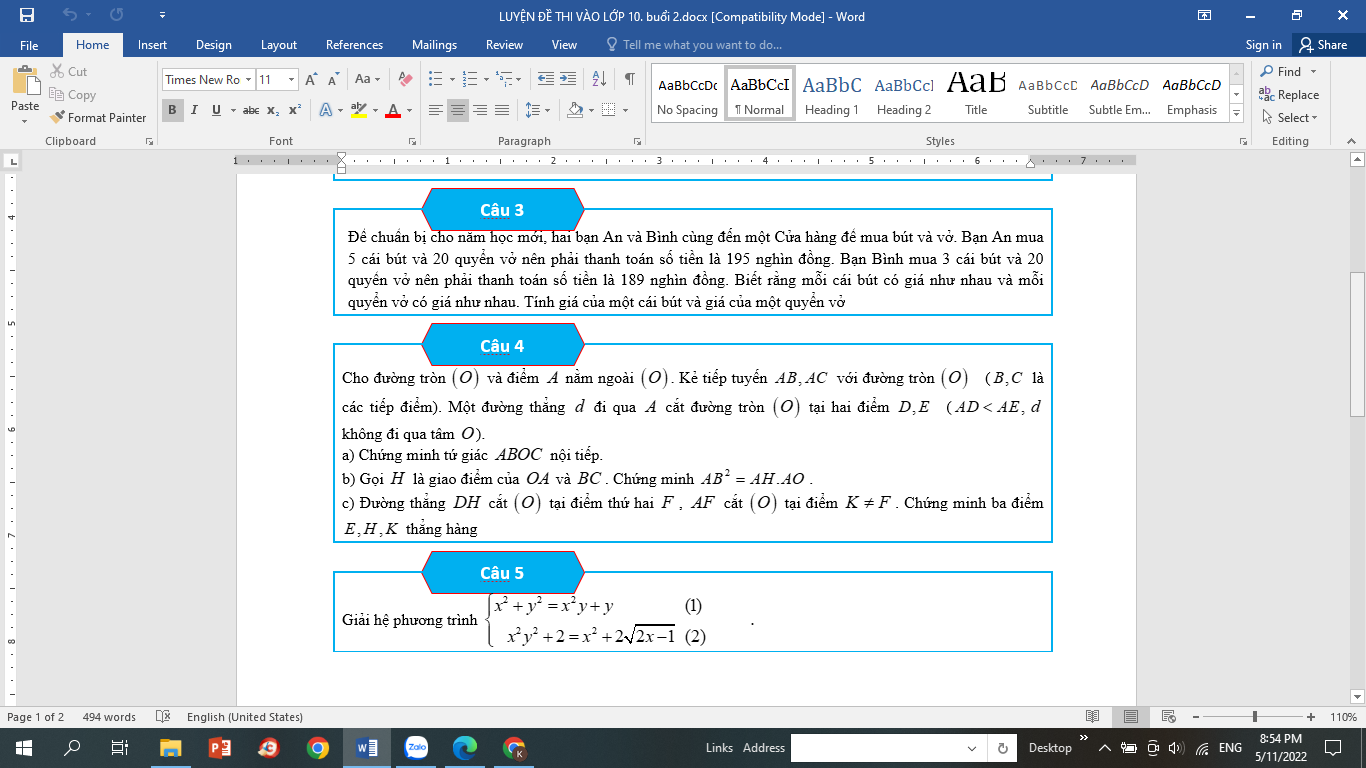



 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!