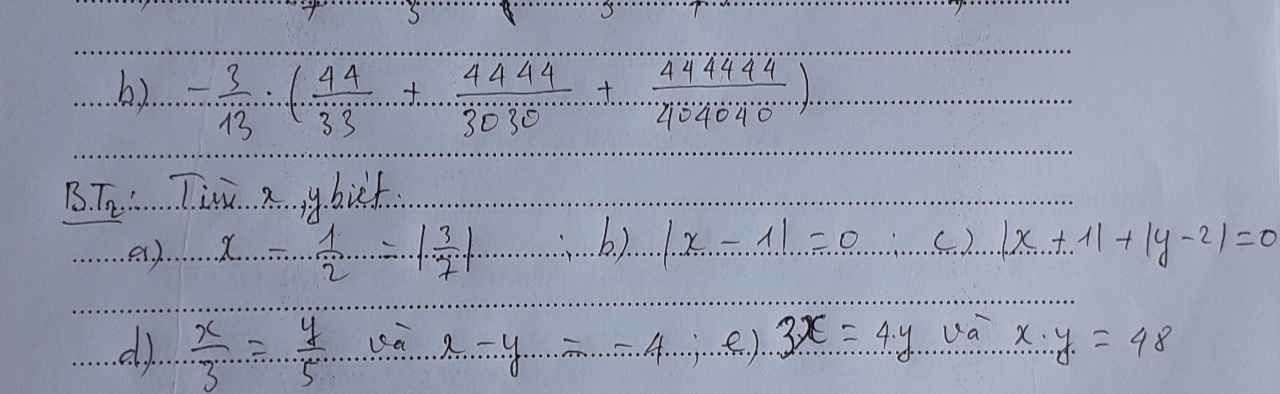a) Ta có: \(x-\dfrac{1}{2}=\left|\dfrac{3}{7}\right|\)
nên \(x-\dfrac{1}{2}=\dfrac{3}{7}\)
hay \(x=\dfrac{3}{7}+\dfrac{1}{2}=\dfrac{6}{14}+\dfrac{7}{14}=\dfrac{13}{14}\)
b) Ta có: |x-1|=0
nên x-1=0
hay x=1
c) Ta có: \(\left|x+1\right|\ge0\forall x\)
\(\left|y-2\right|\ge0\forall y\)
Do đó: \(\left|x+1\right|+\left|y-2\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=-1 và y=2
d) Ta có: \(\dfrac{x}{3}=\dfrac{y}{5}\)
mà x-y=-4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{-4}{-2}=2\)
Do đó: x=6; y=10
e) Ta có: 3x=4y
nên \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}\)
Đặt \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k\\y=\dfrac{1}{4}k\end{matrix}\right.\)
Ta có: xy=48
nên \(\dfrac{1}{3}k\cdot\dfrac{1}{4}k=48\)
\(\Leftrightarrow k^2\cdot\dfrac{1}{12}=48\)
\(\Leftrightarrow k^2=48\cdot12=576\)
hay \(k\in\left\{24;-24\right\}\)
Trường hợp 1: k=24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot24=8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot24=6\end{matrix}\right.\)
Trường hợp 2: k=-24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot\left(-24\right)=-8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot\left(-24\right)=-6\end{matrix}\right.\)
a, Ta có
x- \(\dfrac{1}{2}\)= \(\left|\dfrac{3}{7}\right|\)
⇒ x- \(\dfrac{1}{2}\)= \(\dfrac{3}{7}\)
⇒ x= \(\dfrac{13}{14}\)
Vậy...
b, \(\left|x-1\right|\)= 0
Ta có:
\(\left|x-1\right|\) \(\ge\) 0 với \(\forall\) x
Dấu bằng xảy ra khi:
x- 1= 0
⇒ x= 1
Vậy....
c, \(\left|x+1\right|+\left|y-2\right|=0\)
Ta có:
\(\left|x+1\right|\ge0\) với ∀ x
\(\left|y-2\right|\ge0\) với \(\forall\) y
\(\Rightarrow\)\(\left|x+1\right|\ge0\) + \(\left|y-2\right|\ge0\) ≥ 0 với \(\forall x,y\)
Dấu bằng xảy ra khi:
\(\left\{{}\begin{matrix}\left|x+1\right|=0\\\left|y-2\right|=0\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x+1=0\\y-2=0\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
Vậy.....