Những câu hỏi liên quan
Cho lăng trụ tam giác ABC.A'B'C'. Gọi I, J, K lần lượt là trọng tâm tam giác ABC, A'B'C', ACC'. Gọi M,N,H lần lượt là trung điểm BC, B'C', AC'. Chứng minh (A'JK) song song (AIB')
Từ các đỉnh của tam giác ABC ta kẻ các đoạn thẳng AA',BB',CC' song song cùng chiều, bằng nhau và không nằm trong mặt phẳng của tam giác. Gọi I, G và K lần lượt là trọng tâm của các tam giác ABC, ACC' và A'B'C'
a) Chứng minh (IGK) // (BB'C'C)
b) Chứng minh rằng (A'GK) // (AIB')
Cho hình lăng trụ ABC.A’B’C’. gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. mặt phẳng nào sau đây song song với (IJK)?
A. (ABC)
B. (A’BC’)
C. (BB’C’)
D. (AA’C)
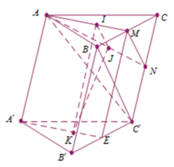
Gọi M, N, E lần lượt là trung điểm của BC, CC′, B′C′.
Suy ra (tính chất trọng tâm tam giác) nên IJ // MN (1).
Trong mặt phẳng (AA′ME) ta có
⇒ IK // ME
mà ME // BB′ nên IK // BB′ (2).
Từ (1) và (2) do (IJK) và (BB′C′) là hai mặt phẳng phân biệt
IJ; IK ∈ (IJK)
Nên IJ // (BB′C′), IK // (BB′C′)
Suy ra (IJK) // (BB′C′)
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
cho tam giác ABC có AB+AC=2BC. Gọi I, G lần lượt là giao điểm của các đường phân giác và trọng tâm tam giác ABC. Chứng minh IG song song với BC
Cho hình lăng trụ ABC.A’B’C’. Gọi I, J, K lần lượt là trọng tâm tam giác ABC, ACC’, A’B’C’. Mặt phẳng nào sau đây song song với (IJK)
A. (BC’A)
B. (AA’B)
C. (BB’C)
D. (CC’A)
cho hình lăng trụ đứng ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC', G là trọng tâm của tam giác A'B'C'. Chứng minh rằng mp(BA'N) song song với mp(MC'G). Ai giúp mk câu này vs mk đang cần gấp
Cho tam giác ABC có BC = 15cm, AC = 18cm, AB = 12cm. Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm tam giác ABC.
a) Chứng minh IG song song với BC.
b) Tính độ dài đoạn thẳng IG.
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và A'B'C'. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là hình gì?
A. Tam giác cân
B. Tam giác vuông
C. Hình thang
D. Hình bình hành
Đáp án D
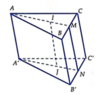
Gọi M là giao điểm của AI và BC; gọi N là giao điểm của A'J và B'C'. Suy ra M,N lần lượt là trung điểm của BC,B'C'.
Ta có M N / / B B ' A A ' / / B B ' ⇒ M N / / A A ' . Mặt khác M N = B B ' ⇒ M N = A A ' .
Từ hai dữ kiện trên suy ra AMNA' là hình bình hành. Vậy thiết diện tạo bởi mặt phẳng (ẠIJ) và hình lăng trụ là hình bình hành.
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác
A
B
C
.
A
B
C
. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và
A
B
C
. Thiết diện tạo bởi mặt phẳng
A
I
J
với hình lăng trụ đã cho là hình gì? A. Tam giác cân B. Tam giác vuông C. Hình thang D. Hình bình hành
Đọc tiếp
Cho hình lăng trụ tam giác A B C . A ' B ' C ' . Gọi I, J lần lượt là trọng tâm của các tam giác ABC và A ' B ' C ' . Thiết diện tạo bởi mặt phẳng A I J với hình lăng trụ đã cho là hình gì?
A. Tam giác cân
B. Tam giác vuông
C. Hình thang
D. Hình bình hành