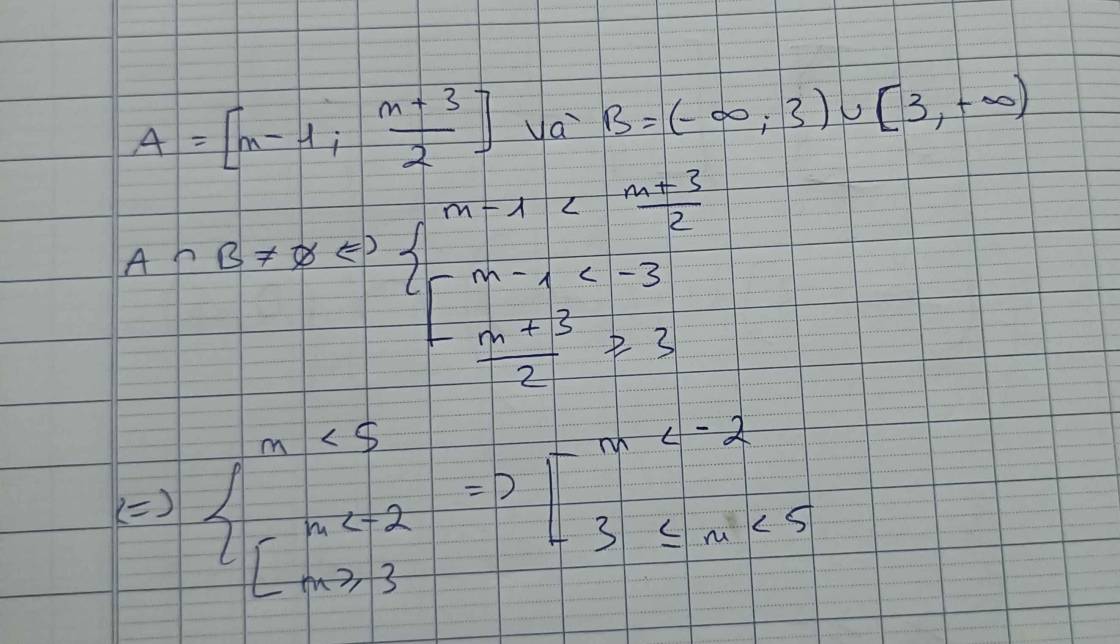Tìm m để tập hợp S= [log2m ; 2m] có không quá 5 phần tử nguyên

Những câu hỏi liên quan
Cho
y
log
2
m
-
3
x
-
m
Tìm m để
y
↑
/
0
;
1
A.
m
3
B.
2
≠
m
3...
Đọc tiếp
Cho y = log 2 m - 3 x - m Tìm m để y ↑ / 0 ; 1
A. m < 3
B. 2 ≠ m < 3
C. 1 ≤ m < 3
D. m ≤ 0 và 1 ≤ m < 3
Tìm m để phương trình
x
4
-
5
x
2
+
4
log
2
m
có 8 nghiệm phân biệt: A.
0
m
2
9
4
B.
-...
Đọc tiếp
Tìm m để phương trình x 4 - 5 x 2 + 4 = log 2 m
có 8 nghiệm phân biệt:
A. 0 < m < 2 9 4
B. - 2 9 4 < m < 2 9 4
C. Không có giá trị của m
D. 1 < m < 2 9 4
Đáp án D
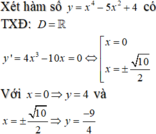


Bước 1: Ta giữ nguyên phần đồ thị phía trên trục hoành.
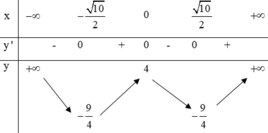
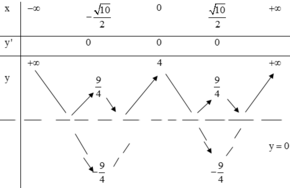
Bước 2: Lấy đối xứng phần phía dưới trục hoành của đồ thị lên phía trên trục hoành và xóa bỏ đi phần đồ thị nằm phía dưới trục hoành ta được đồ thị hàm số y = x 4 - 5 x 2 + 4
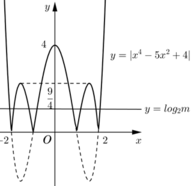
Khi đó số nghiệm của phương trình x 4 - 5 x 2 + 4 = log 2 m chính là số giao điểm của đồ thị hàm số y = x 4 - 5 x 2 + 4 và đường thẳng y = log 2 m với m > 0.Dựa vào đồ thị hàm số y = x 4 - 5 x 2 + 4 ta thấy để phương trình x 4 - 5 x 2 + 4 = log 2 m có 8 nghiệm thì: 0 < log 2 m < 9 4 ⇔ 1 < m < 2 9 4
Đúng 0
Bình luận (0)
Tìm m để phương trình
x
4
−
5
x
2
+
4
log
2
m
có 8 nghiệm thực phân biệt A.
0
m
2
9
4...
Đọc tiếp
Tìm m để phương trình x 4 − 5 x 2 + 4 = log 2 m có 8 nghiệm thực phân biệt
A. 0 < m < 2 9 4
B. − 2 9 4 < m < 2 9 4
C. Không có giá trị của m
D. 1 < m < 2 9 4
Tìm tất cả các giá trị của tham số m để phương trình x3 - 3x - log2m = 0 có đúng một nghiệm.
A. 1/4 < m < 4.
B. 0 < m < 1/4; m > 4.
C. m = 1/4.
D. m < 1/4; m > 4.
Chọn B.
Điều kiện: m > 0
Phương trình tương đương: x3 - 3x = log2m.
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = x3 - 3x với đường thẳng y = log2m (có phương song song trục hoành).
Ta có 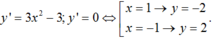
Dựa vào dáng điệu của đồ thị hàm bậc ba, suy ra ycbt 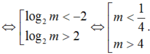
Đối chiếu điều kiện, ta được 0 < m < 1/4 hoặc m > 4.
Đúng 0
Bình luận (0)
Cho phương trình log 2 m = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực
A. m ≥ 0
B. m ∈ R
C. m > 0
D. < 0
Câu 36. Cho các tập hợp khác rỗng [ m−1; m+3 /2 ] và B=(âm vô cùng ; -3) hợp [3;dương vô cùng). Gọi S là tập hợp các giá nguyên dương của m để A giao B ≠ ∅ . Tìm số tập hợp con của S .
gọi S là tập hợp tất cả các giá trị m để phương trình m lnx - x lnm = x-m có 2 nghiệm phân biệt. tìm tập S
Cho hàm số yf(x) có bảng biến thiên như hình dưới đây. Tìm tất cả các giá trị của m để phương trình
f
4
x
-
x
2
log
2
m
có 4 nghiệm thực phân biệt A.
m
∈...
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm tất cả các giá trị của m để phương trình f 4 x - x 2 = log 2 m có 4 nghiệm thực phân biệt
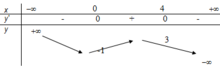
A. m ∈ 0 ; 8 .
B. m ∈ 1 2 ; 8 .
C. m ∈ - 1 ; 3 .
D. m ∈ 0 ; 1 2 .
Cho hàm số
y
-
x
4
+
2
x
2
có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phươngtrình
-
x
4
+
2
x
2
log
2
m
có bốn nghiệm thực phân biệt A.
0
≤
m
≤
1...
Đọc tiếp
Cho hàm số y = - x 4 + 2 x 2 có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phươngtrình - x 4 + 2 x 2 = log 2 m có bốn nghiệm thực phân biệt
A. 0 ≤ m ≤ 1
B. m > 0
C. m ≥ 2
D. 1 < m < 2
Đáp án D
Ta có phương trình - x 4 + 2 x 2 = log 2 m có 4 nghiệm phân biệt
⇔ 0 < log 2 m < 1 ⇔ 1 < m < 2
Đúng 0
Bình luận (0)