a: \(=\dfrac{2x-9-x^2+9+2x^2-4x+x-2}{\left(x-3\right)\left(x-2\right)}\)

\(=\dfrac{x^2-x-2}{\left(x-3\right)\left(x-2\right)}=\dfrac{x+1}{x-3}\)

b: |Q|=1

=>x+1/x-3=1 hoặc x+1/x-3=-1

=>x+1=x-3 hoặc x+1=3-x

=>2x=2 và 1=-3(loại)

=>x=1(nhận)

c: Q nguyên khi x-3+4 chia hết cho x-3

=>\(x-3\in\left\{1;-1;2;-2;4;-4\right\}\)

=>\(x\in\left\{4;;5;1;7;-1\right\}\)

a. ĐKXĐ: \(x\ne\pm1\)

b. \(A=\left(x^2-1\right)\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}-1\right)\)

\(=\left(x-1\right)\left(x+1\right)\left[\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\right]\)

\(=\left(x-1\right)\left(x+1\right)\left[\dfrac{x+1-x+1-\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\right]\)

\(=\left(x-1\right)\left(x+1\right)\left[\dfrac{-x^2+3}{\left(x-1\right)\left(x+1\right)}\right]\)

\(=\dfrac{\left(x-1\right)\left(x+1\right)\left(-x^2+3\right)}{\left(x-1\right)\left(x+1\right)}\)

\(=-x^2+3\)

c. Thay x = 3 vào A ta được:

\(-\left(3\right)^2+3=-6\)

Vậy: Giá trị của A tại x = 3 là -6

a) ĐKXĐ: \(x\ne1;x\ne-1.\)

b) \(A=\left(x^2-1\right).\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}-1\right).\)

\(=\left(x^2-1\right).\dfrac{x+1-x+1-x^2+1}{x^2-1}=-x^2+3.\)

c) Thay x = 3 (TMĐK) vào A: \(-3^2+3=-6.\)

a: ĐKXĐ: x>=0; x<>1

b \(A=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\)

\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\)

\(=\dfrac{1}{\sqrt{x}+2}\)

c: Khi x=9-4 căn 5 thì \(A=\dfrac{1}{\sqrt{5}-2+2}=\dfrac{\sqrt{5}}{5}\)

d: căn x+2>=2

=>A<=1/2

Dấu = xảy ra khi x=0

điều kiện là x chẵn

1. ĐKXĐ: \(x\ne\pm1\)

2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)

\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)

\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)

\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)

\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{x-3}{x-1}\)

3. Tại x = 5, A có giá trị là:

\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)

4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)

Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)

\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)

Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)

Ta có: Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.

Khi đó điều kiện xác định là: 2x - 2 ≠ 0; x 2 - 1 ≠ 0 ; 2x + 2 ≠ 0 hay x ≠ ± 1

Vậy với x ≠ ± 1 thì giá trị của biểu thức xác định.

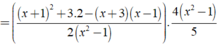
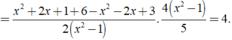
⇒ Giá trị của biểu thức A không phụ thuộc vào biến x

a: ĐKXĐ: x=0; x<>1

\(M=\left(2+\sqrt{x}\right)\left(1-2\sqrt{x}-x+1+\sqrt{x}+x\right)\)

\(=\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)=4-x\)

b: Sửa đề: P=1/M

P=1/4-x=-1/x-4

Để P nguyên thì x-4 thuộc {1;-1}

=>x thuộc {5;3}

\(P=\dfrac{\dfrac{x}{x-2}-\dfrac{x-2}{x+2}}{\dfrac{1}{x^2-4}}\)

a)

Để giá trị của biểu thức P được xác định, thì :

 \(\left[{}\begin{matrix}x-2\ne0\\x+2\ne0\\x^2-4\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne-2\\x\ne-2;2\end{matrix}\right.\)

Vậy ĐKXĐ của biểu thức P là : \(x\ne\left\{2;-2\right\}\)

b)

\(P=\dfrac{\dfrac{x}{x-2}-\dfrac{x-2}{x+2}}{\dfrac{1}{x^2-4}}=\left(\dfrac{x}{x-2}-\dfrac{x-2}{x+2}\right):\dfrac{1}{x^2-4}=\left(\dfrac{x\left(x+2\right)-\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right).\dfrac{x^2-4}{1}\)

\(=\dfrac{x^2+2x-x^2+2x-4}{x^2-4}.\dfrac{x^2-4}{1}=\dfrac{4x-4}{x^2-4}.\dfrac{x^2-4}{1}=4x-4\)

c)

Để : 

\(P=0\Rightarrow4x-4=0\)

\(\Rightarrow4\left(x-1\right)=0\)

\(\Rightarrow x-1=0\)

\(\Rightarrow x=1\)

Vậy.....

ĐK: \(x\ne\pm2\)

\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right).\dfrac{x+2}{2}\)

\(=\left[\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}\right].\dfrac{x+2}{2}\)

\(=\dfrac{x-2x-2+x-2}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{2}\)

\(=\dfrac{2}{2-x}\)