phương trình mx2 + 2( 2m - 3 )x+m2-4=0 có 2 nghiệm trái dấu khi và chỉ khi
Những câu hỏi liên quan
Phương trình
m
2
+
1
x
2
-
x
-
2
m
+
3
0
có hai nghiệm trái dấu khi và chỉ khi: A.
m
2
3
B.
m
3
2
C.
m
3...
Đọc tiếp
Phương trình m 2 + 1 x 2 - x - 2 m + 3 = 0 có hai nghiệm trái dấu khi và chỉ khi:
A. m > 2 3
B. m < 3 2
C. m > 3 2
D. m > - 3 2
Phương trình
(
m
2
+
1
)
x
2
-
x
-
2
m
+
3
0
có hai nghiệm trái dấu khi và chỉ khi A.
m
2
3
B.
m
3
2
C.
m
3
2
D.
m...
Đọc tiếp
Phương trình ( m 2 + 1 ) x 2 - x - 2 m + 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m > 2 3
B. m < 3 2
C. m > 3 2
D. m > - 3 2
Để phương trình đã cho có 2 nghiệm trái dấu khi ac < 0
Hay (m2+ 1). (- 2m + 3 )< 0
Lại có, m2 + 1 > 0 với mọi m
Suy ra: -2m + 3 < 0 ⇔ m > 3 2
Đúng 0
Bình luận (0)
Phương trình x 2 - 2 m + 2 x + m 2 - m - 6 = 0 luôn có hai nghiệm trái dấu khi và chỉ khi
A. m<-2
B. -3<m<2
C. -2
D. -2<m<3
Để phương trình đã cho có hai nghiệm trái dấu khi:
a c = m 2 - m - 6 < 0 ⇔ - 2 < m < 3
Chọn đáp án D.
Đúng 0
Bình luận (0)
Phương trình (m + 2) x 2 - 3x + 2m - 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m<-2
B. -2<m< 3 2
C. ( - ∞ ; - 9 2 ]
D. [ - 9 2 ; + ∞ )
Chọn B.
Phương trình (m + 2) x 2 - 3x + 2m - 3 = 0 có hai nghiệm trái dấu
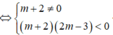
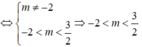
Vậy phương trình (m + 2)
x
2
- 3x + 2m - 3 = 0 có hai nghiệm trái dấu khi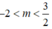 
Đúng 0
Bình luận (0)
Phương trình
m
+
1
x
2
-
x
-
3
m
+
4
0
có hai nghiệm trái dấu khi và chỉ khi A.
m
-
1
hoặc
m
4
3
B.
m
-
1
hoặc
m
3...
Đọc tiếp
Phương trình m + 1 x 2 - x - 3 m + 4 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m < - 1 hoặc m > 4 3
B. m < - 1 hoặc m > 3 4
C. m > 4 3
D. - 1 < m < 4 3
Phương trình
m
+
2
x
2
-
3
x
+
2
m
-
3
0
có hai nghiệm trái dấu khi và chỉ khi A.
m
-
2
B.
-
2
m
3
2
C.
m...
Đọc tiếp
Phương trình m + 2 x 2 - 3 x + 2 m - 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m < - 2
B. - 2 < m < 3 2
C. m > 3 2
D. m < - 2 hoặc m > 3 2
2. Tìm giá trị của m để phương trình sau có 2 nghiệm cùng dấu. Khi đó 2 nghiệm mang dấu gì ? a) x - 2mx + 5m - 4 0 (1) b) ma + mr +3 0 (2) 3. Cho phương trình: (m + 1)x2 + 2(m + 4)x + m+1 0 Tìm m để phương trình có: a) Một nghiệm b) Hai nghiệm phân biệt cùng dấu c) Hai nghiệm âm phân biệt 4. Cho phương trình (m - 4)x2 – 2(m- 2)x + m-1 0 Tìm m để phương trình a) Có hai nghiệm trái dấu và nghiệm âm có GTTÐ lớn hơn b) Có 2 nghiệm trái dấu và bằng nhau về GTTÐ c) Có 2 nghiệm trái dấu d) Có nghiệm...
Đọc tiếp
2. Tìm giá trị của m để phương trình sau có 2 nghiệm cùng dấu. Khi đó 2 nghiệm mang dấu gì ? a) x - 2mx + 5m - 4= 0 (1) b) ma + mr +3 0 (2) 3. Cho phương trình: (m + 1)x2 + 2(m + 4)x + m+1 = 0 Tìm m để phương trình có: a) Một nghiệm b) Hai nghiệm phân biệt cùng dấu c) Hai nghiệm âm phân biệt 4. Cho phương trình (m - 4)x2 – 2(m- 2)x + m-1 = 0 Tìm m để phương trình a) Có hai nghiệm trái dấu và nghiệm âm có GTTÐ lớn hơn b) Có 2 nghiệm trái dấu và bằng nhau về GTTÐ c) Có 2 nghiệm trái dấu d) Có nghiệm kép dương. e) Có một nghiệm bằng 0 và một nghiệm dương.
Bất phương trình
log
2
2
x
-
(
2
m
+
5
)
log
2
x
+
m
2
+
5
+
4
0
nghiệm đúng với mọi
x
∈
[
2
;
4
)
khi và chỉ khi A.
m
∈
[
0...
Đọc tiếp
Bất phương trình log 2 2 x - ( 2 m + 5 ) log 2 x + m 2 + 5 + 4 < 0 nghiệm đúng với mọi x ∈ [ 2 ; 4 ) khi và chỉ khi
A. m ∈ [ 0 ; 1 )
B. m ∈ [ - 2 ; 0 )
C. m ∈ ( 0 ; 1 ]
D. m ∈ ( - 2 ; 0 ]
Có yêu cầu bài toán tương đương với:
log 2 2 x - ( 2 m + 5 ) log 2 x + m 2 + 5 m + 4 < 0 ∀ x ∈ [ 2 ; 4 )
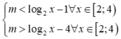
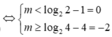
⇔ m ∈ [ - 2 ; 0 )
Chọn đáp án B.
*Chú ý bấm máy phương trình bậc hai
có hai nghiệm
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho phương trình
(m2 +m +1) x2 -(m2 +2m+2) x-1=0
a) chứng tỏ rằng phương trình có hai nghiệm trái dấu.
b) gọi x1, x2 là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất và nhỏ nhất của tổng: s= x1 +x2
a) Xét pt đã cho có \(a=m^2+m+1\); \(b=-\left(m^2+2m+2\right)\); \(c=-1\)
Nhận thấy rằng \(ac=\left(m^2+m+1\right)\left(-1\right)=-\left(m^2+m+1\right)\)
\(=-\left(m^2+2m.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)=-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Vì \(-\left(m+\dfrac{1}{2}\right)^2\le0\) và \(-\dfrac{3}{4}< 0\) nên \(-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\) hay \(ac< 0\). Vậy pt đã cho luôn có 2 nghiệm trái dấu.
b) Theo câu a, ta đã chứng minh được pt đã cho luôn có 2 nghiệm trái dấu \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m^2+2m+2\right)}{m^2+m+1}=\dfrac{m^2+2m+2}{m^2+m+1}\)
Nhận thấy \(m^2+m+1\ne0\) nên ta có:
\(\left(m^2+m+1\right)S=m^2+2m+2\) \(\Leftrightarrow Sm^2+Sm+S-m^2-2m-2=0\)\(\Leftrightarrow\left(S-1\right)m^2+\left(S-2\right)m+\left(S-2\right)=0\)(*)
pt (*) có \(\Delta=\left(S-2\right)^2-4\left(S-1\right)\left(S-2\right)\)\(=S^2-4S+4-4\left(S^2-3S+2\right)\)\(=S^2-4S+4-4S^2+12S-8\)\(=-3S^2+8S-4\)
Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(-3S^2+8S-4\ge0\)\(\Leftrightarrow-3S^2+6S+2S-4\ge0\)\(\Leftrightarrow-3S\left(S-2\right)+2\left(S-2\right)\ge0\) \(\Leftrightarrow\left(S-2\right)\left(2-3S\right)\ge0\)
Ta xét 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}S-2\ge0\\2-3S\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\ge2\\S\le\dfrac{2}{3}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}S-2\le0\\2-3S\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\le2\\S\ge\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\dfrac{2}{3}\le S\le2\) (nhận)
Khi \(S=\dfrac{2}{3}\) thì (*) \(\Leftrightarrow\left(\dfrac{2}{3}-1\right)m^2+\left(\dfrac{2}{3}-2\right)m+\dfrac{2}{3}-2=0\)\(\Leftrightarrow-\dfrac{1}{3}m^2-\dfrac{4}{3}m-\dfrac{4}{3}=0\)\(\Leftrightarrow m^2+4m+4=0\)
\(\Leftrightarrow\left(m+2\right)^2=0\) \(\Leftrightarrow m+2=0\) \(\Leftrightarrow m=-2\)
Khi \(S=2\) thì (*) \(\Leftrightarrow\left(2-1\right)m^2+\left(2-2\right)m+2-2=0\)\(\Leftrightarrow m^2=0\)
\(\Leftrightarrow m=0\)
Vậy GTNN của S là \(\dfrac{2}{3}\) khi \(m=-2\) và GTLN của S là \(2\) khi \(m=0\)
Đúng 0
Bình luận (0)