Giải phương trình
( \(x^2\)- \(2x\)+\(1\) ) - \(4=0\)
1/ Chứng minh phương trình vô nghiệm:
a) \(-16x^2-8x+4=0\)
b) \(-x^2+4x-4=0\)
2/ Giải phương trình sau:
\(\left(x^2-2x-4\right)\left(2x^2-8x-1\right)=0\)
Bài 1:
b: \(\Leftrightarrow x-2=0\)
hay x=2
Bài 1:giải các phương trình sau:
a) (x-3).(x+7)=0 b) (x-2)^2+(x-2).(x-3)=0 c)x^2-5x+6=0
Bài 2:giải các phương trình chứa ẩn ở mẫu sau:
a)x/x+1-1=3/2x b)4x/x-2-7/x=4
Bài 3:giải phương trình sau
a)2x^2-5x-7=0 b)1/x^2-4+2x/x-2=2x/x+2
giúp mình với,mình đang cần gấp
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
Bài 2.
a) \(\frac{x}{x+1}-1=\frac{3}{2}x\)
ĐKXĐ : x khác -1
<=> \(\frac{x}{x+1}-\frac{x+1}{x+1}=\frac{3}{2}x\)
<=> \(\frac{-1}{x+1}=\frac{3x}{2}\)
=> 3x( x + 1 ) = -2
<=> 3x2 + 3x + 2 = 0
Vi 3x2 + 3x + 2 = 3( x2 + x + 1/4 ) + 5/4 = 3( x + 1/2 )2 + 5/4 ≥ 5/4 > 0 ∀ x
=> phương trình vô nghiệm
b) \(\frac{4x}{x-2}-\frac{7}{x}=4\)
ĐKXĐ : x khác 0 ; x khác 2
<=> \(\frac{4x^2}{x\left(x-2\right)}-\frac{7x-14}{x\left(x-2\right)}=\frac{4x^2-8x}{x\left(x-2\right)}\)
=> 4x2 - 7x + 14 = 4x2 - 8x
<=> 4x2 - 7x - 4x2 + 8x = -14
<=> x = -14 ( tm )
Vậy phương trình có nghiệm x = -14
Giải phương trình và hệ phương trình:
1) \(-2x^2+x+1-2\sqrt{x^2+x+1}=0\)
2) \(\left\{{}\begin{matrix}x^4+y^3x+x^2y^2=3y^4\\2x^2+y^4+1=2x\left(y^2+1\right)\end{matrix}\right.\)
1) \(-2x^2+x+1-2\sqrt[]{x^2+x+1}=0\)
\(\Leftrightarrow2\sqrt[]{x^2+x+1}=-2x^2+x+1\left(1\right)\)
Ta có :
\(2\sqrt[]{x^2+x+1}=2\sqrt[]{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\ge\sqrt[]{3}\)
Dấu "=" xảy ra khi và chỉ khi \(x+\dfrac{1}{2}=0\Leftrightarrow x=-\dfrac{1}{2}\)
\(\left(1\right)\Leftrightarrow-2x^2+x+1=\sqrt[]{3}\)
\(\Leftrightarrow2x^2-x+\sqrt[]{3}-1=0\)
\(\Delta=1-8\left(\sqrt[]{3}-1\right)=9-8\sqrt[]{3}\)
\(pt\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt[]{9-8\sqrt[]{3}}}{4}\left(loại\right)\\x=\dfrac{1-\sqrt[]{9-8\sqrt[]{3}}}{4}\left(loại\right)\end{matrix}\right.\) \(\left(vì.x=-\dfrac{1}{2}\right)\)
Vậy phương trình cho vô nghiệm
Giải các phương trình sau:
a) 2 x − 1 = 2 x − 5 ; b) 7 − x − 2 − 3 x = 0 ;
c) x − 4 + x 2 − 5 x + 4 = 0 ; d) x 2 − x − 2 x + 1 − x = 0 .
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
1)giải phương trình
( x^2 - 2x +1 ) - 4 =0
Ta có: \(\left(x^2-2x+1\right)-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-2^2=0\)
\(\Leftrightarrow\left(x-1-2\right)\left(x-1+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy: S={3;-1}
Giải phương trình : 4x2 - 4x - 5|2x-1| - 5 = 0
Giải bất phương trình : (2x2 + 3x + 4)2 - (x2 +x +4)2 >0
\(4x^2-4x-5\left|2x-1\right|-5=0\)
\(\Leftrightarrow-5\left|2x-1\right|=5-4x^2+4x\)
\(\Leftrightarrow\left|2x-1\right|=\frac{-4x^2+4x+5}{-5}\)
\(\Leftrightarrow\left|2x-1\right|=\frac{4x\left(x-1\right)}{5}-1\)
TH1 : \(2x-1=\frac{4x\left(x-1\right)}{5}-1\Leftrightarrow2x=\frac{4x\left(x-1\right)}{5}\)
\(\Leftrightarrow10x=4x^2-4x\Leftrightarrow14x-4x^2=0\)
\(\Leftrightarrow-2x\left(2x-7\right)=0\Leftrightarrow x=0;x=\frac{7}{2}\)
TH2 : \(2x-1=-\left(\frac{4x\left(x-1\right)}{5}-1\right)\Leftrightarrow2x-1=-\frac{4x\left(x-2\right)}{5}+1\)
\(\Leftrightarrow2x-2=-\frac{4x\left(x-2\right)}{5}\Leftrightarrow10x-10=-4x^2+8x\)
\(\Leftrightarrow2x-10+4x^2=0\Leftrightarrow2\left(2x^2+x-5\ne0\right)=0\)tự chứng minh
Vậy tập nghiệm của phương trình là S = { 0 ; 7/2 }
giải phương trình sau:
\(x^2+2x+6-2\sqrt{2x-1}-4\sqrt{x^2+3}=0\)
Giải phương trình
a ) 2 x + 3 x - 4 = 2 x - 1 x + 2 - 27
b ) x 2 - 4 - x + 5 2 - x = 0
c ) x + 2 x - 2 - x - 2 x + 2 = 4 x 2 - 4
d ) x + 1 x - 1 - x + 2 x + 3 + 4 x 2 + 2 x - 3 = 0
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
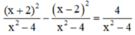
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
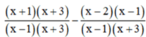
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)
\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)
\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)
\(< =>\left(x-2\right)\left(2x+7\right)=0\)
\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)